If in previous illustration, The charge particle is projected at angle $α$ with x-axis with magnitude of velocity. Find
a. velocity vector in function of time $\to v (t) .$
b. position vector in function of time $\to r (t) .$

Video Solution

Text Solution

Verified by Experts

We can make components of the velocity of the particle along x-axis and y-axis. The component which is along the magnetic field will remain unchanged. But the component perpendicular to the magnetic field will provide circular motion. In a combined way, the path of the particle will be helical.

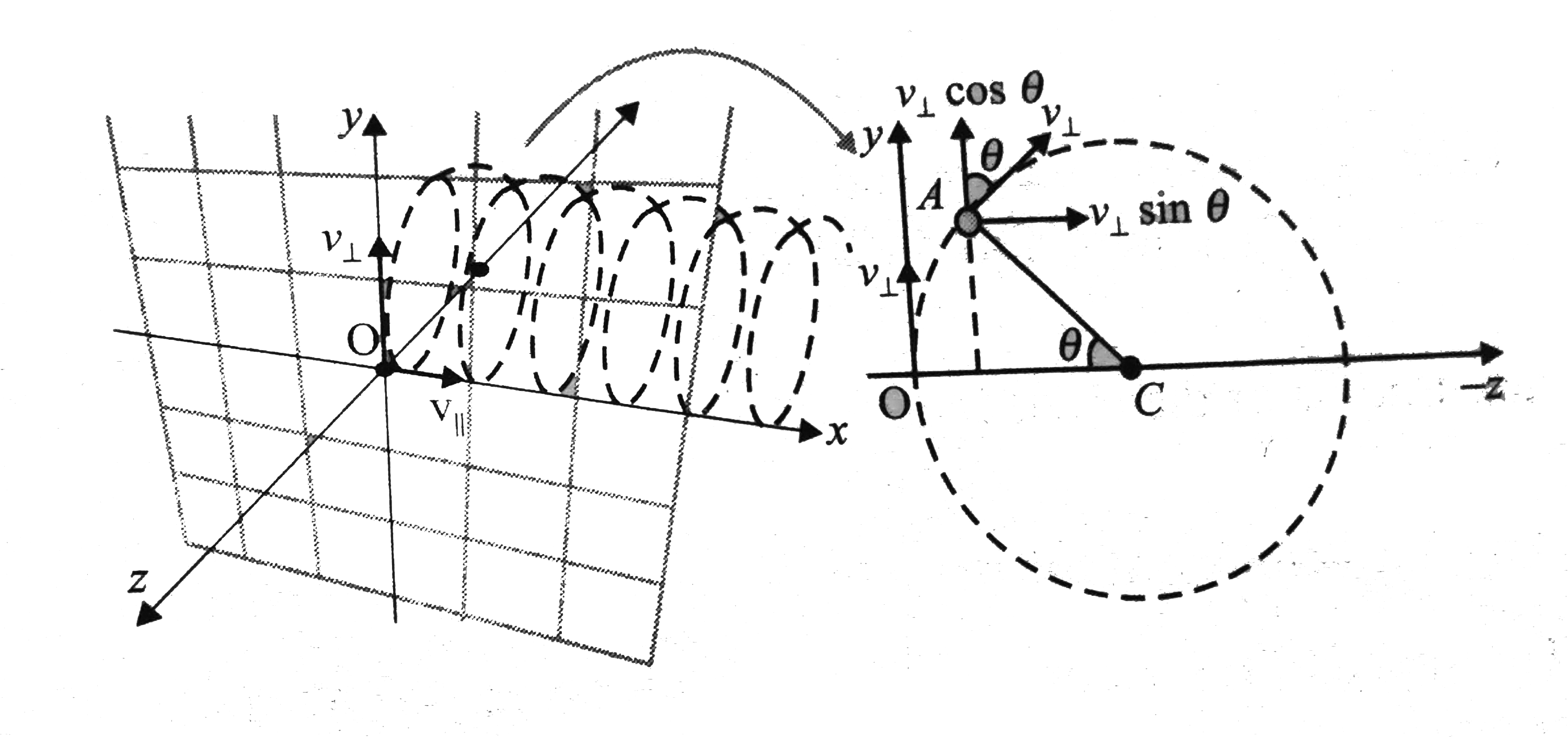
The component of velocity parallel to magnetic field
$v_{∣ ∣} = v cos α$
The component of velocity perpendicular to magnetic field
$v_{⊥} = v sin α$
The y and z components of velocity and position vector can be calculated in the same way as in previous illustration. The only difference is in place of v we substitute $v_{⊥}$ . Hence, velocity vector $[{\to v}_{⊥} (t)]$ in function of time can be writtens as
${\to v}_{⊥} (t) = v_{⊥} cos . \frac{q B}{m} t ˆ j - v_{⊥} sin . \frac{q B}{m} t ˆ k$
Hence net velocity
$\to v = v_{∣ ∣} ˆ i + v_{⊥} cos . \frac{q B}{m} t ˆ j - v_{⊥} sin . \frac{q B}{m} t ˆ k$
And position vector in function of time
$\to r (t) = v_{∣ ∣} t ˆ i + R sin . \frac{q B t}{m} ˆ j - R (1 - cos . \frac{q B t}{m}) ˆ k$ .

Updated on:21/07/2023

A particle I projected at an angle of elevation $α$ after time $t$ it makes an angle $β$ with horizontal. The velocity of projection is
A $\frac{2 g t cos β}{sin (α - β)}$
B $\frac{g t cos β}{sin (α - β)}$
C $\frac{g t}{2 sin (α - β)}$
D $\frac{4 g t}{sin (α - β)}$
A projectill is projected at an angle $(α > 45^{\circ})$ with an initial velocity u. The time t, at which its magnitude of horizontal velocity will equal the magnitude of vertical velocity is :-
A $t = \frac{u}{g (cos α - sin α)}$
B $t = \frac{u}{g (cos α + sin α)}$
C $t = \frac{u}{g (sin α - cos α)}$
D $t = \frac{u}{g ({sin}^{2} α - {cos}^{2} α)}$
The velocity vector of the motion described by the position vector of a particle, $r = 2 t ˆ i + t^{2} ˆ j$ is given by
A $v = 2 ˆ i + 2 t ˆ j$
B $v = 2 t ˆ I + 2 t ˆ j$
C $v = t ˆ i + t^{2} ˆ j$
D $v = 2 ˆ i + t^{2} ˆ j$