A conductor (rod) of mass m, length l carrying a current i is subjected to a magnetic field of induction B. If the coefficients of friction between the conducting rod and rail is μ, find the value of I if the rod starts sliding.
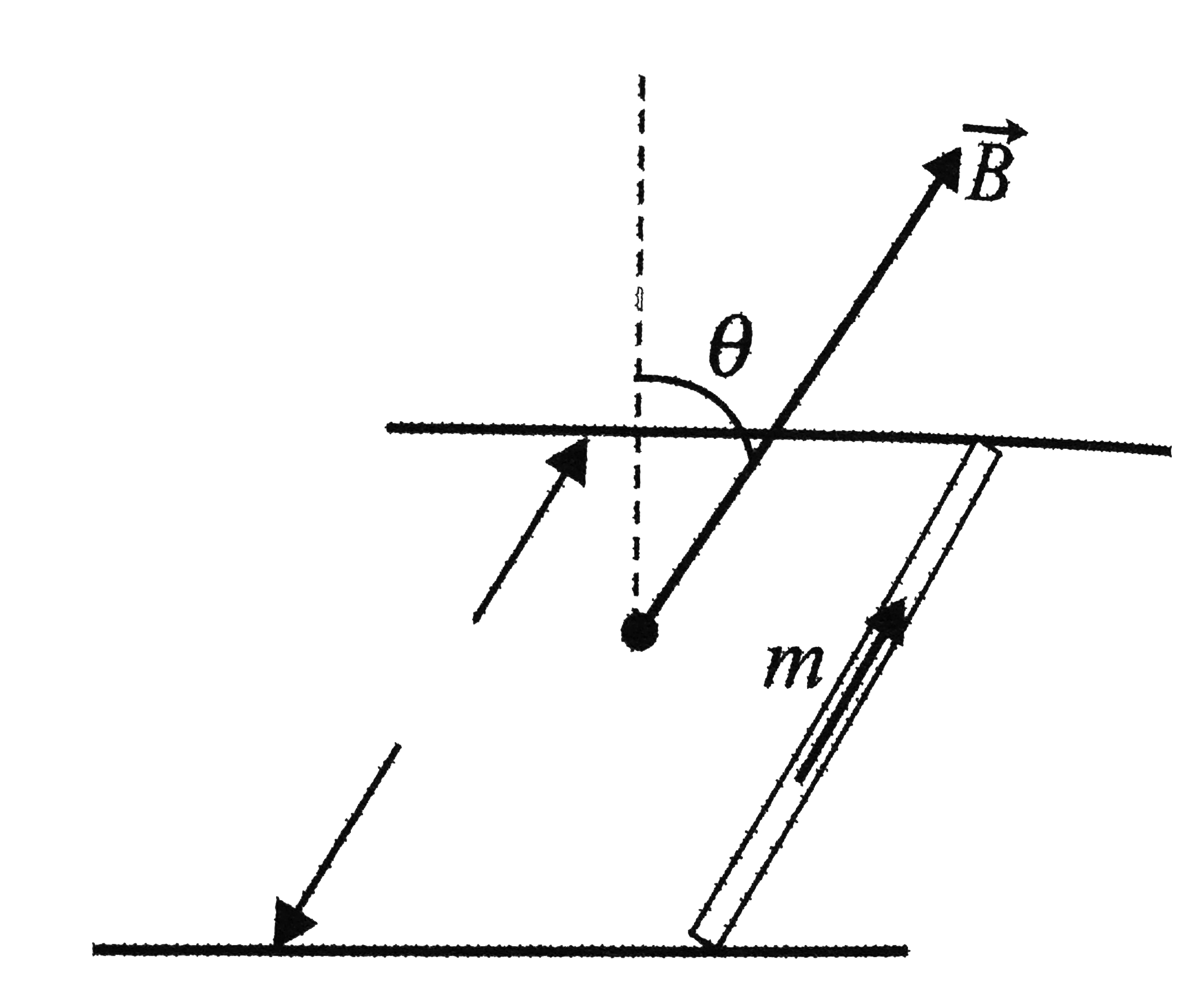
The magnetic force is Fm=ilBsinφ,
where φB =Angle between current and magnetic field =90∘.
or Fm=ilB
but it acts at an angle θ with horizontal as shown in Fig. according to Fleming's left hand rule.
Then the net force along x- and y-axis are
Fy=N−(mg+Fmsinθ)=0
or N=mg+Fmsinθ....(i)
Fx=f−Fmcosθ=0....(ii)
or f=Fmcosθ
Law of friction, f=μN....(iii)
By using the above equations
μ(mg+Fmsinθ)=Fmcosθ
or Fm=μmgcosθ−μsinθorilB=μmgcosθ−μsinθ
or i=μmglB(cosθ−μsinθ)
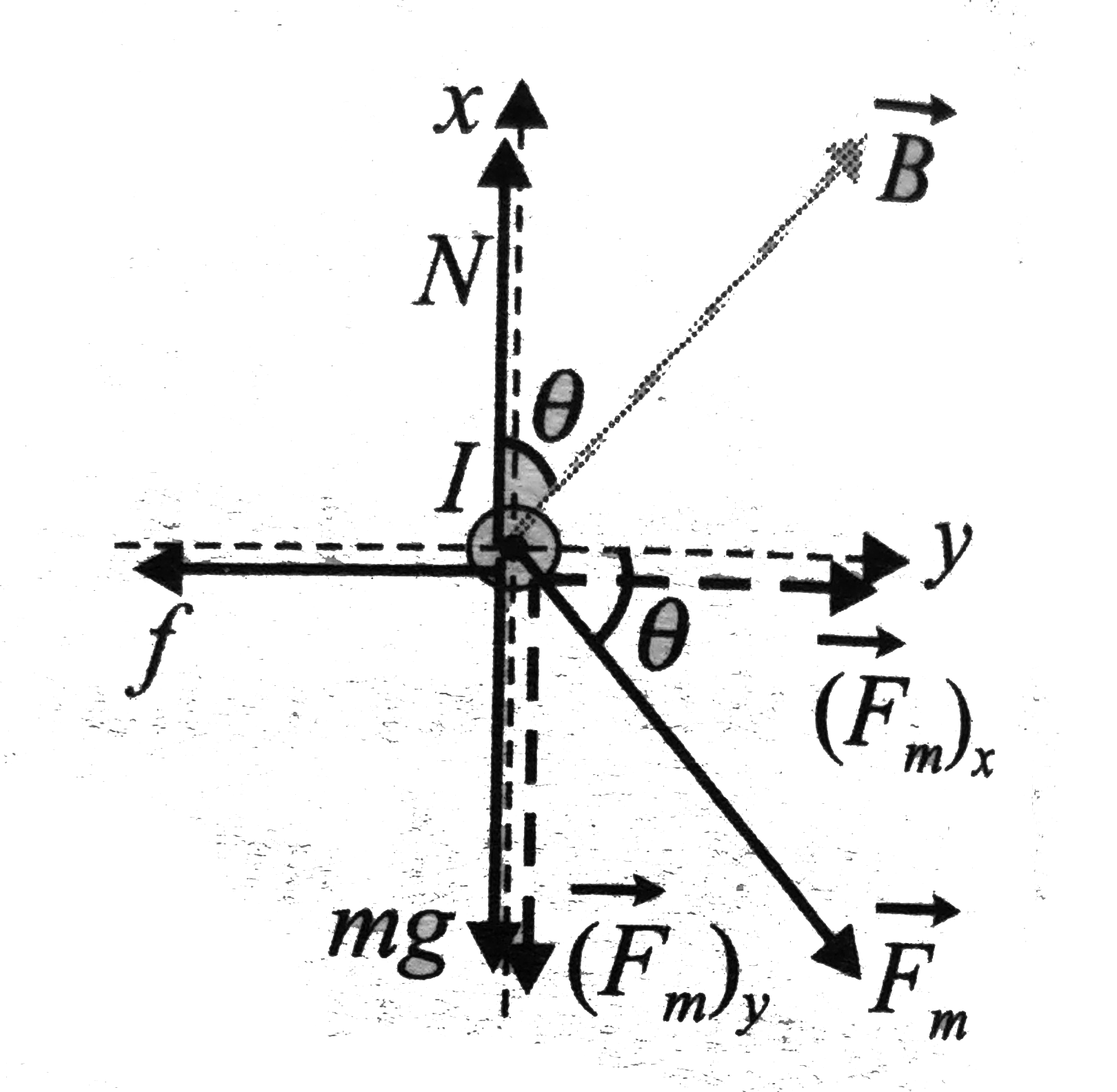 .
.
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Solved Example
25 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.1
22 Videos
- KINETIC THEORYBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORYEXERCISE - Question Bank
31 Videos
- Magnetism and MatterBOOK - CENGAGE PHYSICSCHAPTER - Magnetism and MatterEXERCISE - Question Bank
50 Videos
Similar Questions
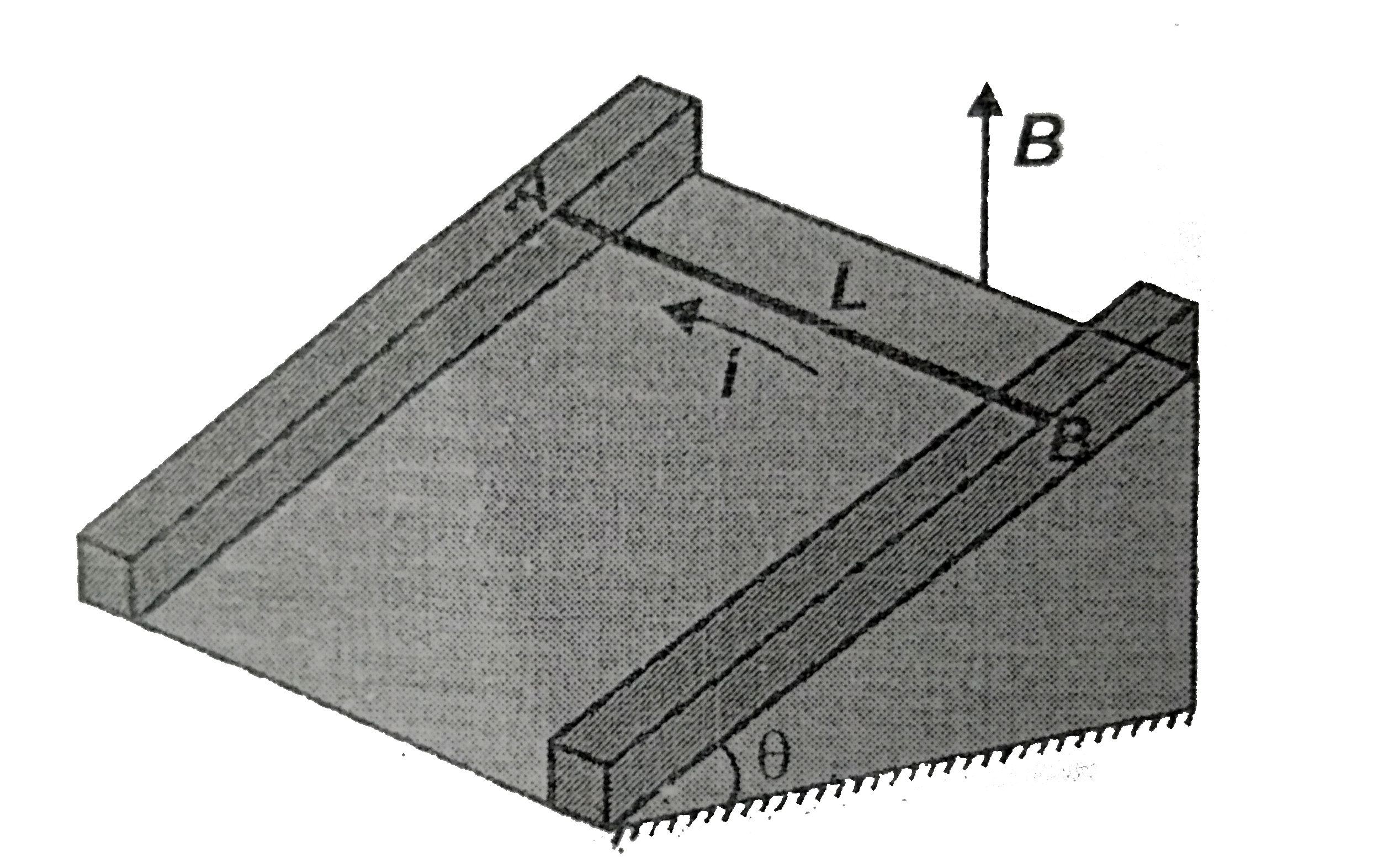
On an inclined plane, two conducting rails are fixed along the line of greatest slope. A conducting rod AB is placed on the radils so that it is horizontal. A vertically upward uniform magnetic field is present in the region. A current i flows through AB from B to A. The mass of AB is m and the coefficient of friction between the rod and rails is μ. Find the minimum and maximum value of B, so that the rod can stay in equilibrium. Assume that μ<tanθ
View SolutionA rod of mass M and length L lies on an incline having inclination of θ=37∘. The coefficient of friction between the rod and the incline surface is μ=0.90. Find the tension at the mid point of the rod.
View Solution
Knowledge Check
When a conductor of length l carrying a current I is placed in a magnetic field of induction B at an angle θ with respect to →B, the force experienced by it is
AF=IBlBF=IBlsinθCF=IBlcosθDF=IBltanθPQ is a uniform rod of length l and mass m carrying current i and is suspended in uniform magnetic field of induction →B acting inward as shown in figure. The tension in each string is
 Amg−BilBmg+BilCmg−Bil2Dmg+Bil2
Amg−BilBmg+BilCmg−Bil2Dmg+Bil2
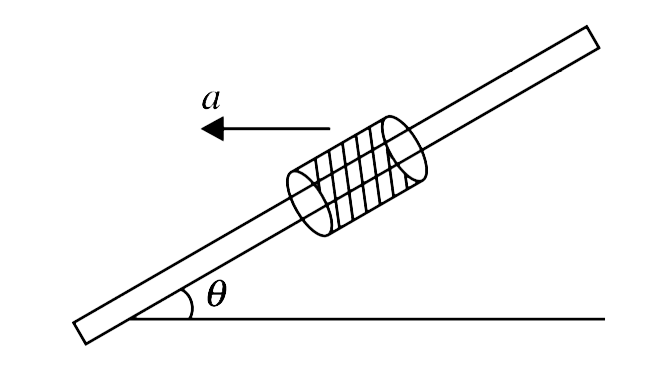
A rod is kept inclined at an angle θ with the horizontal A sleeve of mass m can slide on the rod. If the coefficient of friction between the rod and the sleeve is μ, for what values of horizontal acceleration a of the rod, towards left, the sleeve will not slide over the rod?
View SolutionA conducting rod of length 'l'=2√5 meter and mass 'm'=4kg lies on the horizontal table. Coefficient of friction between the rod and the table is 'μ'=(12). If the current in the conductor si 2 ampere, then find the minimum magnitude of magnetic field strength (in Tesla) such that conducting rod just starts to translate along x -axis (take g=10m/sec2) [neglect the radius of rod]

View SolutionA small collar of mass m = 100 g slides over the surface of a horizontal circular rod of radius R = 0.3 m. The coefficient of friction between the rod and the collar is μ=0.8. Find the angle made with vertical by the force applied by the rod on the collar when speed of the collar is V = 2 m/s.

View SolutionA rod CD of length b carrying a current I2 is placed in a magentic field due to a thin long wire AB carrying current I1 as shown in figure. Then find the net force experience by the wire
View SolutionA uniform rod is made to lean between a rough vertical wall and the ground. The coefficient of friction between the rod and the ground is μ1 and between the rod and the wall is μ2. Find the angle at which the rod can he leaned without slipping.
View SolutionA copper rod of mass m rests on two horizontal rails distance L apart and carries a current of I from one rail to the other. The coefficient of static friction between rod and rails is μs What are the (a) magnitude and (b) angle (relative to the vertical) of the smallest magnetic field that puts the rod on the verge of sliding?
View Solution
