Calculate the magnetic field at point O for the current-carrying wire segment shown in Fig. The wire consists of two straight portions and a circular arc of radius a, which subtends an angle θ.
The magnetic field at O due to the current in the straight
segments AA' and CC' is zero because d→s׈r=0 for these paths.
Because we can ignore segments AA' and CC', this example is
categorized as an application of the
Biot -Savart law to the curved wire
segment AC.
Each length element d→s along path
Ac is at the same distance a from O,
and the current in each contributes
a field element d→Bdirected into the pate at O. Furthermore, at every
point on AC, d→s is perpendicular
to ˆr, hence, |d→s׈r|=ds
From the above equation, find the magnitude of the field at O
due to the current in an element of length ds:
dB=μ04πIdsa2

Integrating this expression over the curved path AC, nothing that I
and a are constants:
B=μ0I4πa2∫ds=μ0I4πa2s
From teh geometry, note that s 5 au and substitute:
B=μ0I4πa2(aθ)=μ0I4πaθ
The above equation gives the magnitude of the magnetic field
at O. The direction of →B is into the page at O because d→s׈r
is into the page for every length element.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Solved Example20videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.135videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK12videos
SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITS
- BOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank40videos
THERMAL PROPERTIES OF MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
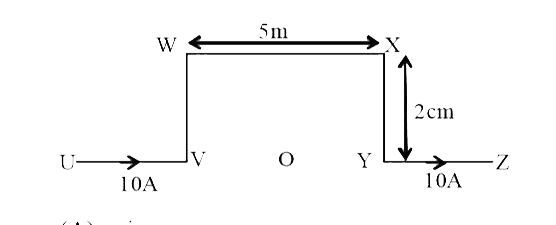
The resulting magnetic field at the point O due to the current carrying wire shown in the figure:
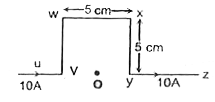 APoints out of the pageBpoints into the pageCis zeroDis the same as due to the segment WX along.
APoints out of the pageBpoints into the pageCis zeroDis the same as due to the segment WX along. - Question 2 - Select One
The magnetic field lines due to a straight wire carrying a current are
AstraightBcircularCparabolicDelliptical - Question 3 - Select One
The strength of the magnetic field at a point r near a long straight current carrying wire is B. The field at a distance r2 will be
AB2BB4C2BD4B
Find the direction of magnetic field at a point P due to two infinite current carrying wires shown in the figure below
 View Solution
View SolutionDraw the magnetic field lines due to a straight wire carrying current.
View SolutionCalculate the force on a current carrying wire in a uniform magnetic field as shown in Fig. 1.59.
 View Solution
View SolutionCalculate magnetic induction at point O if the wire carrying
a current I has the shape shown in Fig.
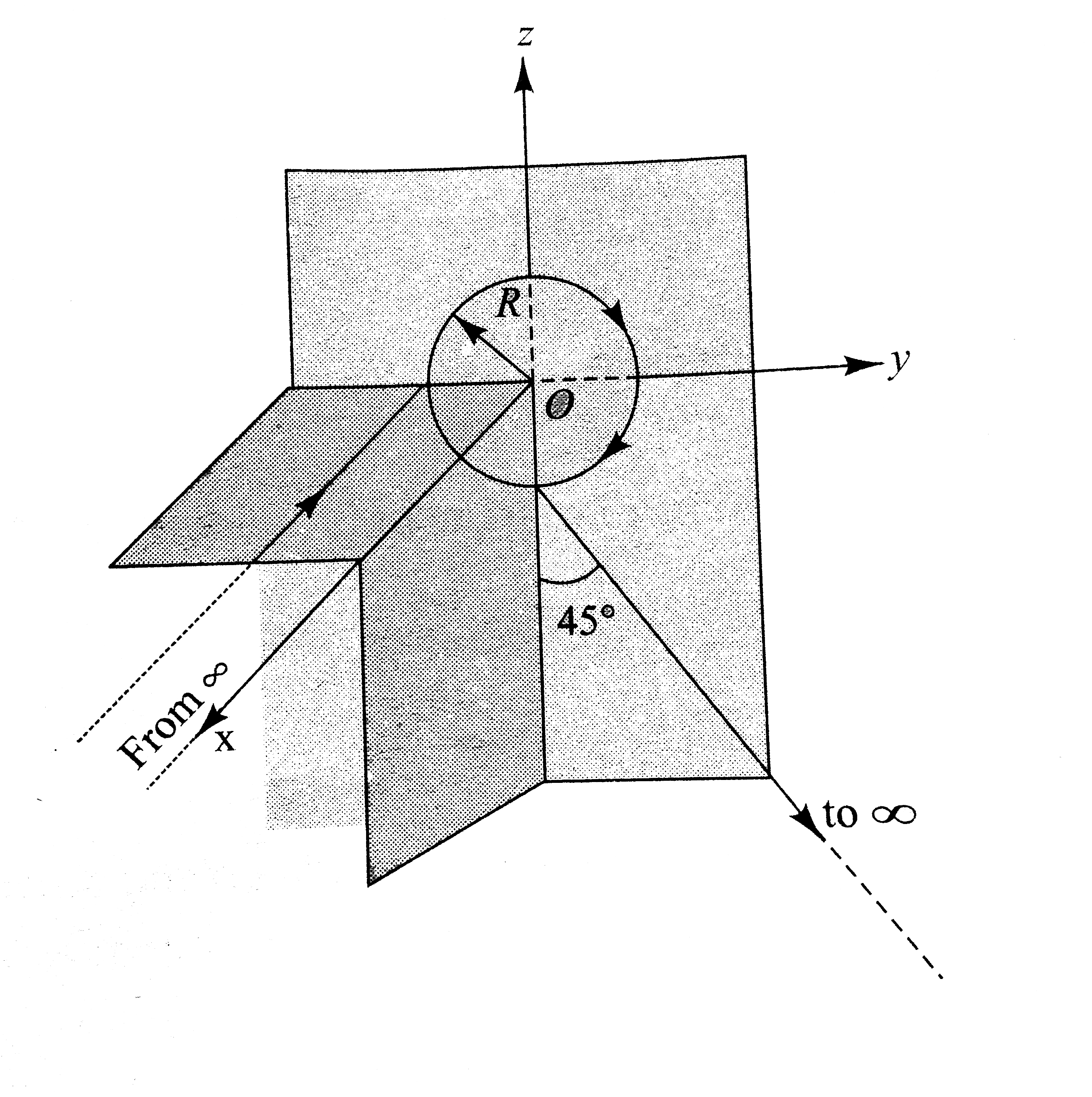
(The radius of the curved part of the wire is equal to R and linear parts of the wire are very long.)View SolutionThe magnetic field at the centre O of the circular portion of radius 3cm carrying current 4 ampere in the wire is
 View Solution
View Solution