Figure shows two current carrying wires piercing the plane of an imaginary loop. One of the wires is normal to the plane of the loop while the other is at an angle. Calculate the net current enclosed.

The current enclosed is simply I1+I2. There is no need to
take any component of I2 perpendicular to the plane of the loop.
All that matters is just the magnitude of the net charge per unit
time that crosses the plane of the loop.
Just as in the case of Gauss's law, the selection of the Amperian
loop is critical for easy application o fhte law. The general rules
while selecting the loop are :
⋅ Estimate the direction of the magnetic field around the
current carrying conductor.
⋅ The loop should include the current carrying element whose
magnetic field is to be calculated.
⋅ The magnetic field should be constant over the whole loop
or should be easy to calculate on the different portions of
the loop.
⋅ The dot product ∮→B.→dl should be easy to calculate.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Solved Example20videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.135videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK12videos
SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITS
- BOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank40videos
THERMAL PROPERTIES OF MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
In Fig. there is a conducting loop ABCDEF of resistance λ per unit length placed near a long straight current-carrying wire. The dimension are shows in the figure. The long wire lies in the plane of the loop. The current in the long wire varies as I=I0(t).

The emf induced in the closed loop isAμ0I0a2πIn(2a+ll)Bμ0I0a2πIn(2a−ll)Cμ0I0aπIn(a+ll)Dμ0aπIn(a+ll) - Question 2 - Select One
In Fig. there is a conducting loop ABCDEF of resistance λ per unit length placed near a long straight current-carrying wire. The dimension are shows in the figure. The long wire lies in the plane of the loop. The current in the long wire varies as I=I0(t).
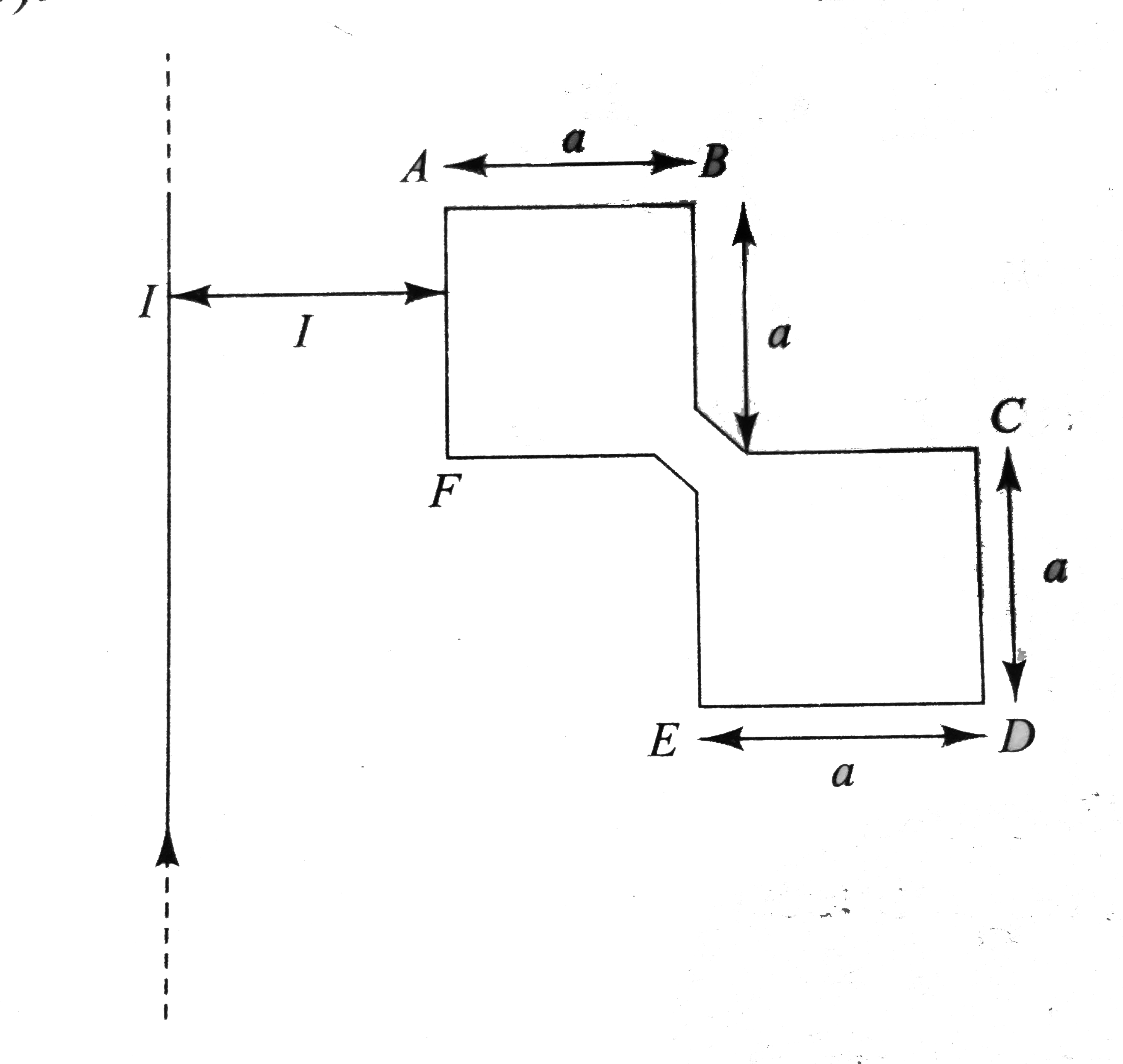
The heat produced in the loop in time t isA[μ0I02πIn(a+ll)]2at4λB[μ0I02πIn(2a+ll)]2at8λC[μ0I02πIn(a+ll)]2at3λD[μ0I02πIn(3a+ll)]2at6λ - Question 3 - Select One
The figure shows a circular loop of radius a with two long parallel wires (νmbered1and2) all in the plane of the paper . The distance of each wire from the centre of the loop is d. The loop and the wire are carrying the same current I. The current in the loop is in the counterclockwise direction if seen from above.
(q) The magnetic fields(B) at P due to the currents in the wires are in opposite directions.
(r) There is no magnetic field at P.
(s) The wires repel each other.
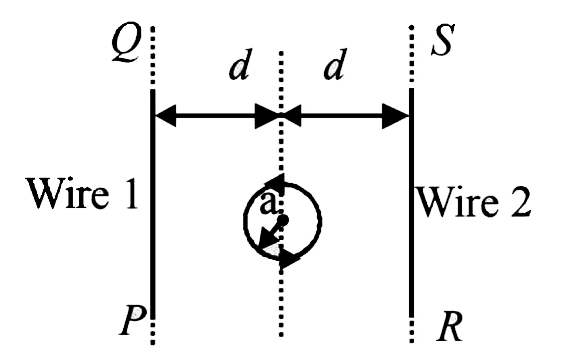
(4) When d≈a but wires are not touching the loop , it is found that the net magnetic field on the axis of the loop . In that caseA(a) current in wire 1andwire2 in the direction PQandRS, respectively and h≈aB(b) current in wire 1andwire2 in the direction PQandSR, respectively and h≈aCcurrent in wire 1andwire2 in the direction PQandSR, respectively and h≈1.2aDcurrent in wire 1andwire2 in the direction PQandRS, respectively and h≈1.2a
An infinitely long current carrying wire and a small current carrying wire and a small current carrying loop are in the plane of thye paper as shown. The ardius of the loop is a and distance of its centre from the wire is d (dgtgta). If the loop applies a force F on the wire then :
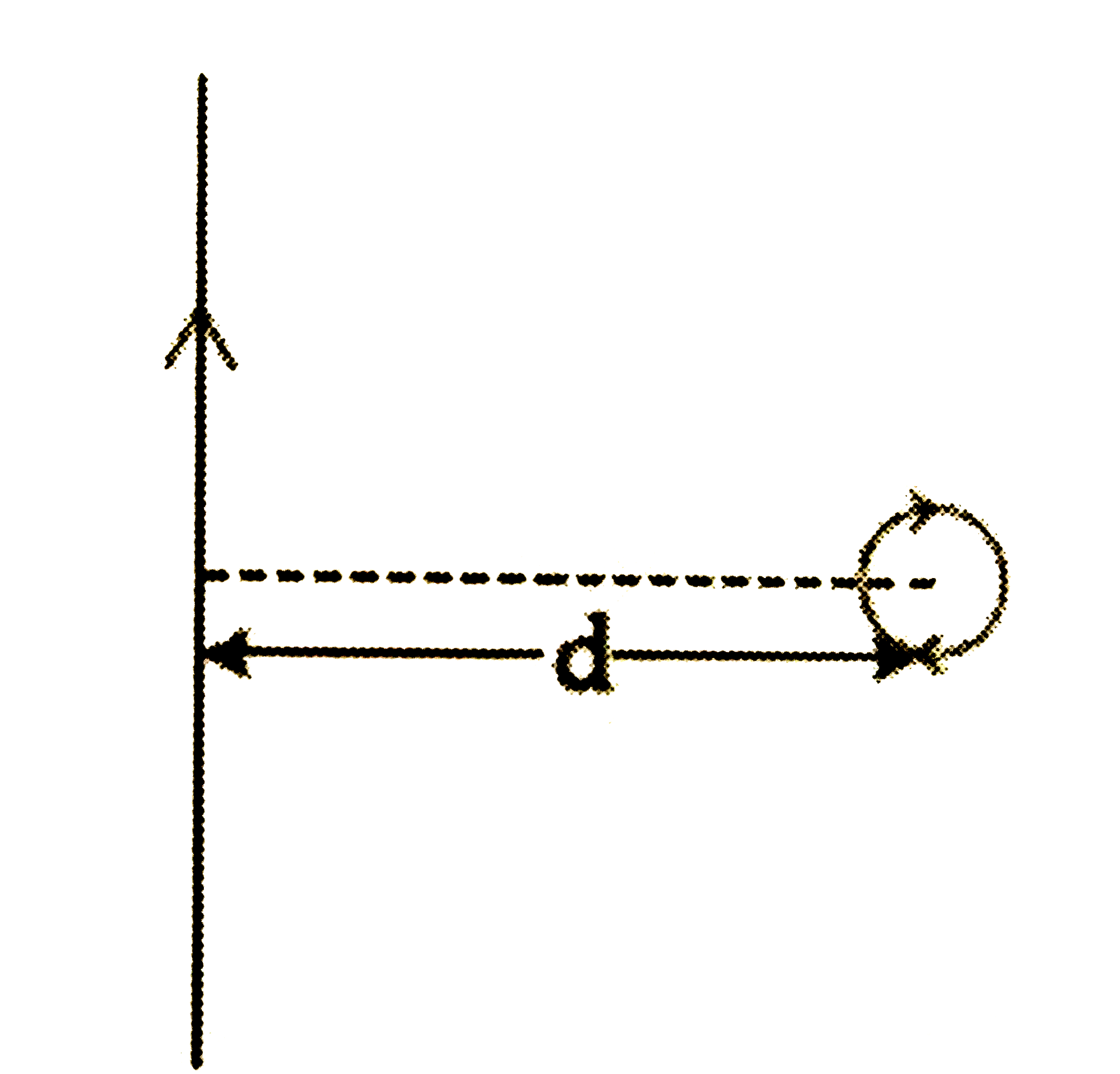 View Solution
View SolutionIn Fig. there is a conducting loop ABCDEF of resistance λ per unit length placed near a long straight current-carrying wire. The dimension are shows in the figure. The long wire lies in the plane of the loop. The current in the long wire varies as I=I0(t).

The mutual inductance of the pair isView SolutionThe figure shows a circular loop of radius a with two long parallel wires (νmbered1and2) all in the plane of the paper . The distance of each wire from the centre of the loop is d. The loop and the wire are carrying the same current I. The current in the loop is in the counterclockwise direction if seen from above.
(q) The magnetic fields(B) at P due to the currents in the wires are in opposite directions.
(r) There is no magnetic field at P.
(s) The wires repel each other.

(4) When d≈a but wires are not touching the loop , it is found that the net magnetic field on the axis of the loop . In that caseView SolutionA current- carrying straight wire is kept along the axis of a circular loop carrying a current. The straight wire
View SolutionA current-carrying, straight wire is kept along the axis of a square loop carrying a current.The straight wire
View Solution