A current I flows along a round loop. Find the integral along the axis of the loop within the range from to . Explain the result obtained.
The magnetic field at point P on the axis of a coil at distance
from the centre of the coil is
the axis of the loop is taken along the x-axis.

The integral on the LHS can be thought of as the line integral of
B over a closed path (a straight line from to and a semi-
circle of infinite radius where the magnetic field vanishes). Then
as per Amper's law, this must be times the current enclosed
by the path which is I.
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.1
35 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.2
10 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
- SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK
12 Videos
- THERMAL PROPERTIES OF MATTERBOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank
40 Videos
Similar Questions
A current I flows along a round loop. Find the intergal ∫Bdr along the axi so the loop within the range from −∞ to +∞. Expain the result obtained.
View SolutionA small current-carrying coil having a megantic moment pm is located at the axis of a round loop of radius R with current I flowing thorough it. Find the magnitude of the vector force applied to the coil if its distance from the centre of the loop is equal to x and the vector pm coincides in direction with the axis of the loop.
View Solution
Knowledge Check
A current I flows along a round circular loop of radius R. Find the line integration of magnetic field along the axis of the loop from center to ∞
Aμ0IB4μ0ICμ0I2Dμ0I4A current 1 flows along a triangle loop having sides of equal length a. The strength of magnetic field at the centre of the loop is :
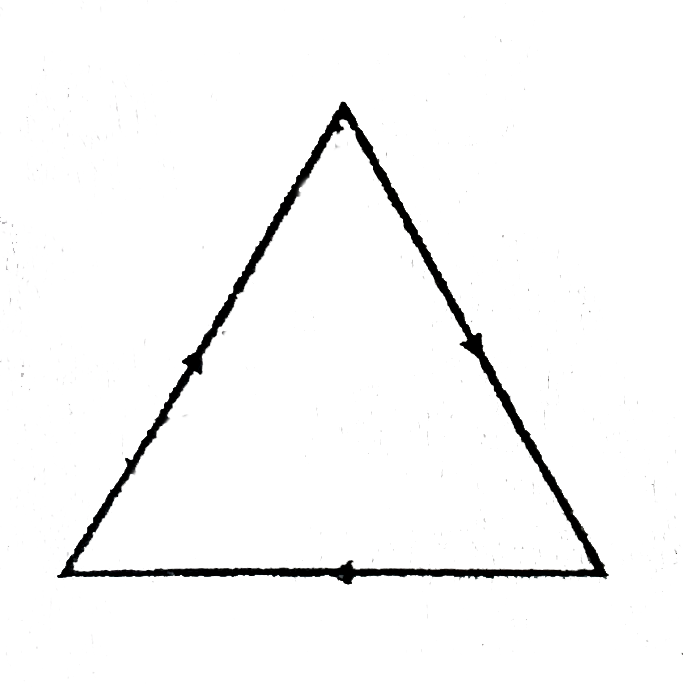 A3μ012πaB9μ0I2πaC(3√3μ0I)/(2πa)D3μ0I4πa
A3μ012πaB9μ0I2πaC(3√3μ0I)/(2πa)D3μ0I4πaA current 1 flows along a triangle loop having sides of equal length a. The strength of magnetic field at the centre of the loop is :
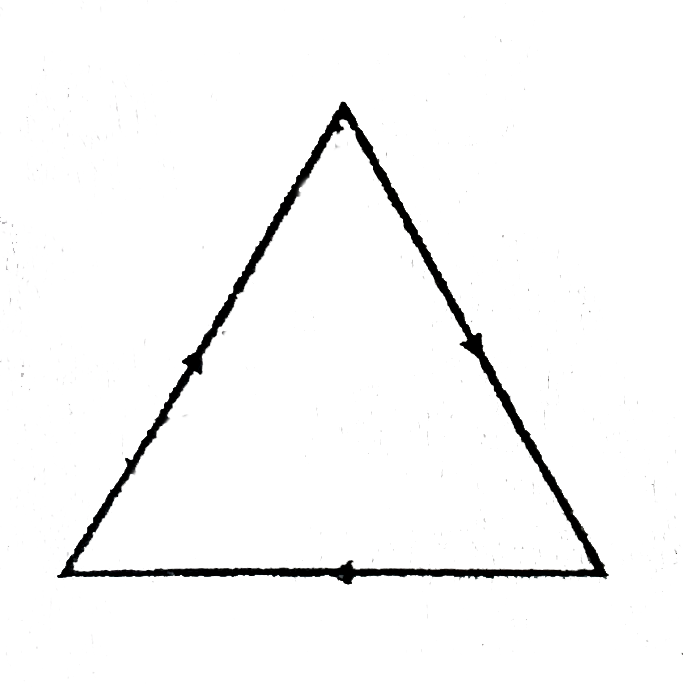 A3μ0I2πaB9μ0I2πaC3√3μ0I2πaD3μ0I4πa
A3μ0I2πaB9μ0I2πaC3√3μ0I2πaD3μ0I4πa
There is one circular current carrying loop. A charged particle is projected with a certain speed along the axis of the coil. How will the coil exert magnetic force on the charged particle?
View SolutionA current I flows along a thin-walled, long, half-cylinder of radius R(figure) Find the magnetic induction at a point on the axis of the cylinder
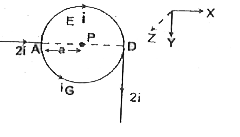
View SolutionIn the shown figure a current 2i is flowing in a straight conductor and entering along the diameter of the circular loop of similar conductor through the point A. The current is leaving the loop along another similar semi-infinite conductor parallel to the plane of the loop through the point D. what is the magnetic field at the centre of the loop P ?
View SolutionA current I flows along a straight conductor with round cross-section. Find the flux of the Poynting vector across the lateral surface of the conductor's segment with resistance R.
View SolutionA: In any magnetic field region the line integral ∮→B.→dl along a closed loop is always zero.
R: The magnetic field →B in the expressioin ∮→B.→dl is due to the currents enclosed only by the loop.
View Solution
