Calculate the magnetic field at point O in each of the following cases:





Video Solution
Text Solution
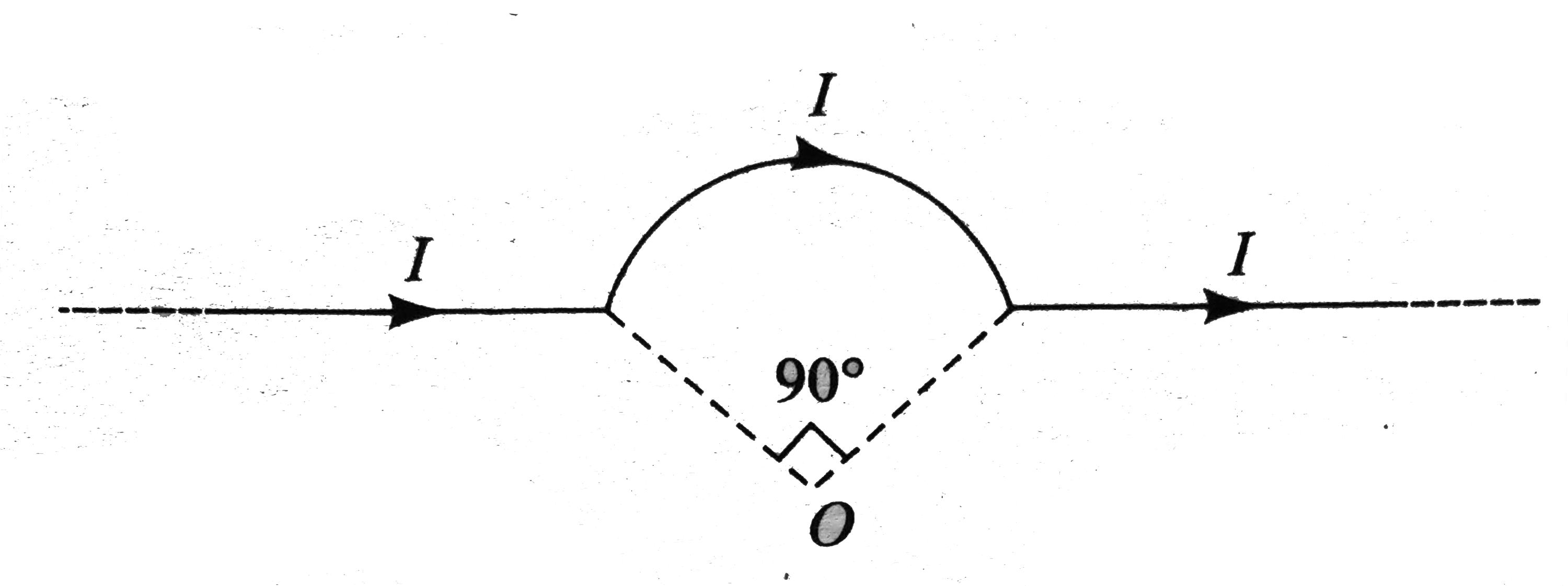
(a) 
Magnetic field due to straight wires=0.
Magnetic field due to a semicircular wire
Bsemicircular=μ0I2R(θ2π)=μI2R(π2π)
or Bsemicircular=μ0I4R
The direction can be verified from the right hadn rule that
will be down ward into the plane of the page.
(b) 
Magnetic field due to straight wire 1-2 will be zero. as in its
direction is passing through centre of the circular wire.
Magnetic field due to circular part
Bcircular=μ0I2R(θ2π)=μ0I2R((3/2)π2π)
Bcircular=3μ0I8R⊗
Magnetic field due to semi-infinite wire 3-4,
Bstraight=μ0I4πR⊗
Net magnetic field at O
B0=3μ0I8R+μ0I4πR
B0=μ0I4πR(32+1π)⊗
(c) 
Magnetic field at O
→B0=→Bcircle+→Bstraight=μ0I2R⊙+μ0I2πR⊙
⇒B=μ0I2R(1+1π)⊙
(d) The magnetic field due to straight wires
will be zero. Magnetic field due to circular
part
Bcircular=μ0I2R(θ2π)=μ0I2R((3/2)π2π)=3μ0I8R⊗
(e) →BR=(μ0I4πR+μ0I4R+μ0I4πR)(−ˆk)=μ0I2R(1π+12)ˆk

|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.210videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (subjective )10videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Solved Example20videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK12videos
SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITS
- BOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank40videos
THERMAL PROPERTIES OF MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
The magnetic field at O is
 AzeroB1C2D3
AzeroB1C2D3 - Question 2 - Select One
The magnetic field at O is
 Aμ0I2R√(14+1π2)Bμ0I2R√(12+1π2)Cμ0IR√(14+1π2)Dμ0IR√(14+1π)
Aμ0I2R√(14+1π2)Bμ0I2R√(12+1π2)Cμ0IR√(14+1π2)Dμ0IR√(14+1π) - Question 3 - Select One
Find magnetic field at O.
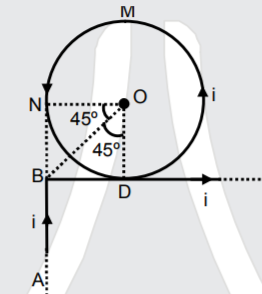 Aμ0i2πR[−1√2+π]Bμ0i2πR[π−1]Cμ0i2RDμ0i2πR[1√2+π]
Aμ0i2πR[−1√2+π]Bμ0i2πR[π−1]Cμ0i2RDμ0i2πR[1√2+π]
Find the magnetic field at point P in following cases
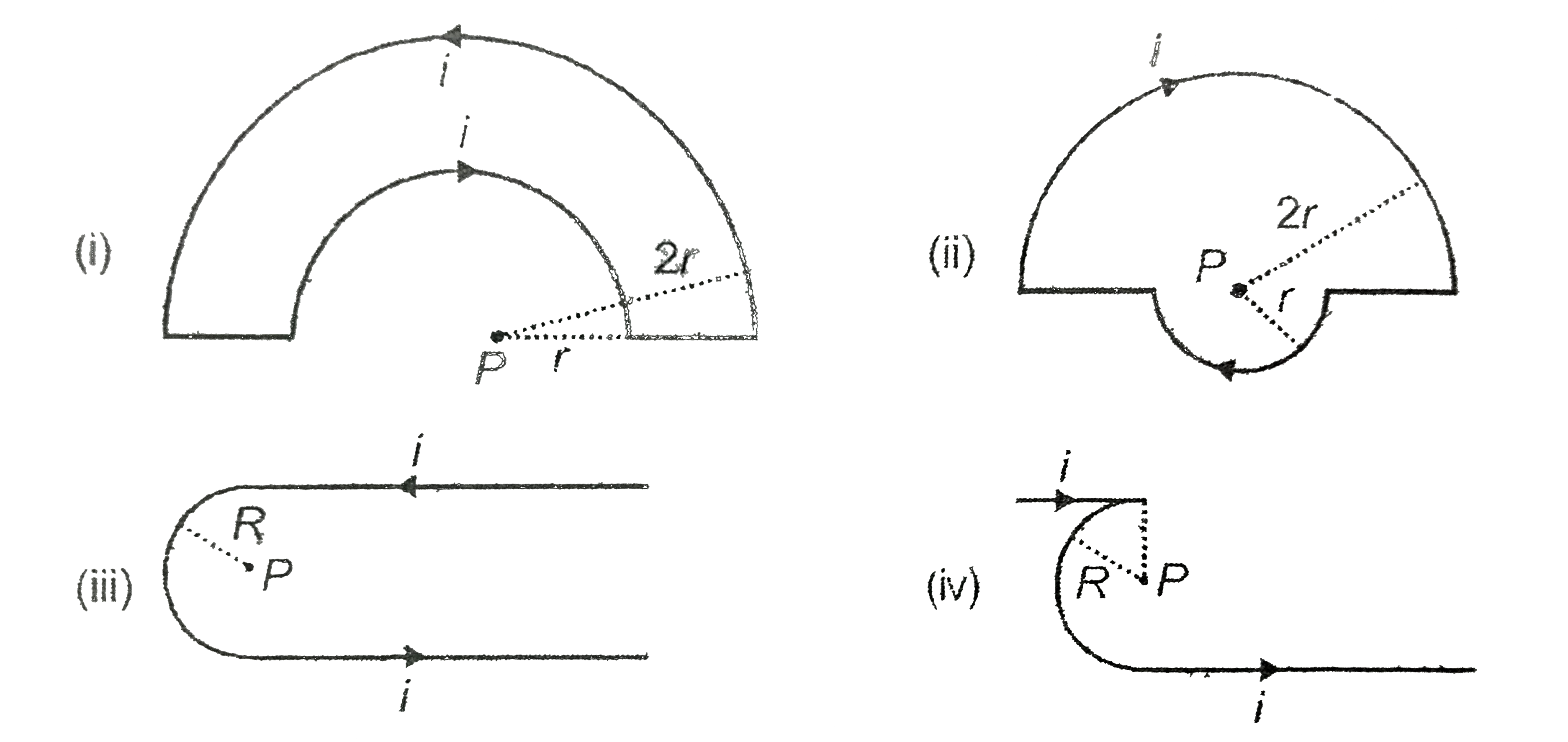 View Solution
View SolutionFind the magnetic field at point O shown in the figure
 View Solution
View SolutionEvaluate magnitude and direction of magnetic field at a point P in the following cases
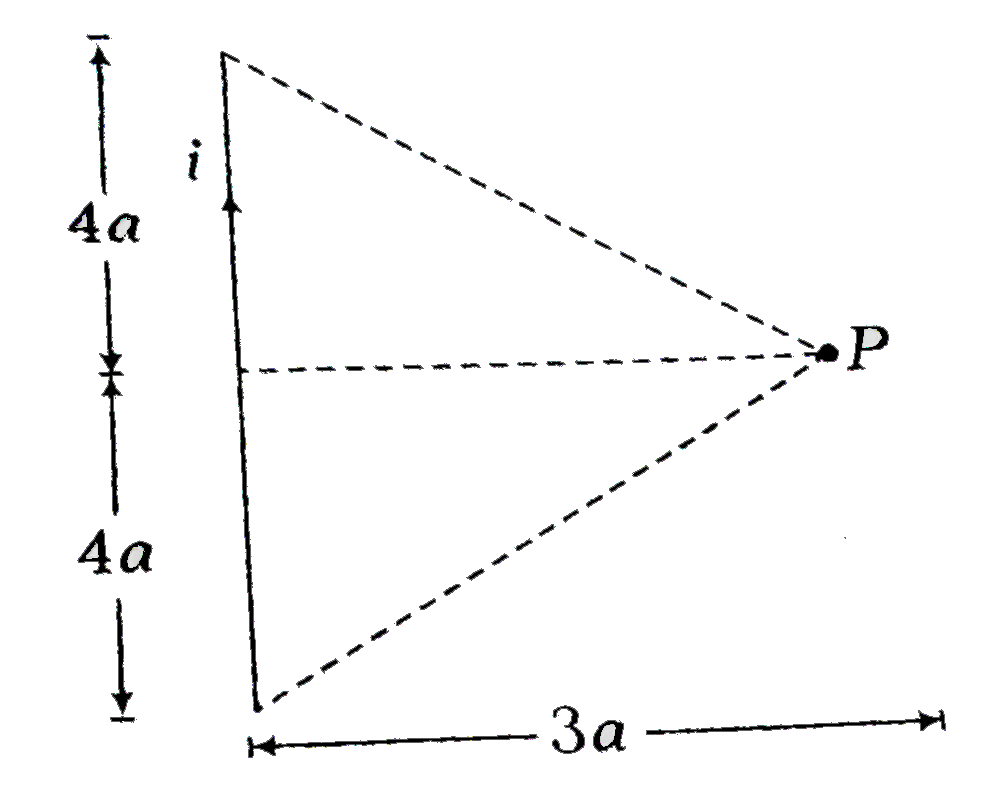
 View Solution
View SolutionMagnetic field at point O due to the given structure is
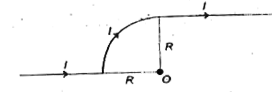 View Solution
View SolutionThe magnetic field at centre O of the arc in Fig.
 View Solution
View Solution


