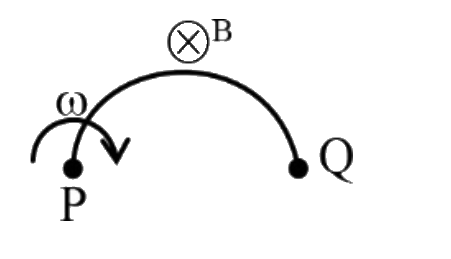
A wire is in the form of a semicircle of radius r. One end is attached to an axis about which it rotates with an angular speed ω. The axis is normal to the plane of the semicircle. The wire is immersed in a uniform magnetic field B parallel to the axis. find the induced emf between points o and P of the semicircle.

It is given that the magnetic field is uniform.
Join the end points O and P and replace the semicircle by a straight rod of length 2r.
We now have a straight rod rotating in a uniform magnetic field in a plane perpendicular to the magnetic field.
Therefore, the induced emf between O and P will be
ξ∈d=12Bω(2r)2=Bωr2
From the right hand rule, we see that elcetrons will accumulate at end O. Therefor, end P is at a higher potential than O.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Solved Example
5 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 3.1
15 Videos
- ELECTROMAGENTIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGENTIC INDUCTIONEXERCISE - QUESTION BANK
40 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
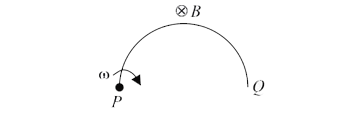
A wire is bent to form a semicircle of the radius a. The wire rotates about its one end with angular velocity ω . Axis of rotation is perpendicular to the plane of the semicircle . In the space , a uniform magnetic field of induction B exists along the aixs of rotation as shown in the figure . Then -
View SolutionA wire is bent to form a semi-circle of radius a. The wire rotates about its one end with angular velocity ω. Axis of rotation being perpendicular to plane of the semicircle. In the space, a uniform magnetic field of induction exists along the axis of rotation as shown. The correct statement is
View Solution
Knowledge Check
A straight wire of length L is bent into a semicircle. It is moved in a uniform magnetic field with speed v with diameter perpendicular to the field. The induced emf between the ends of the wire is
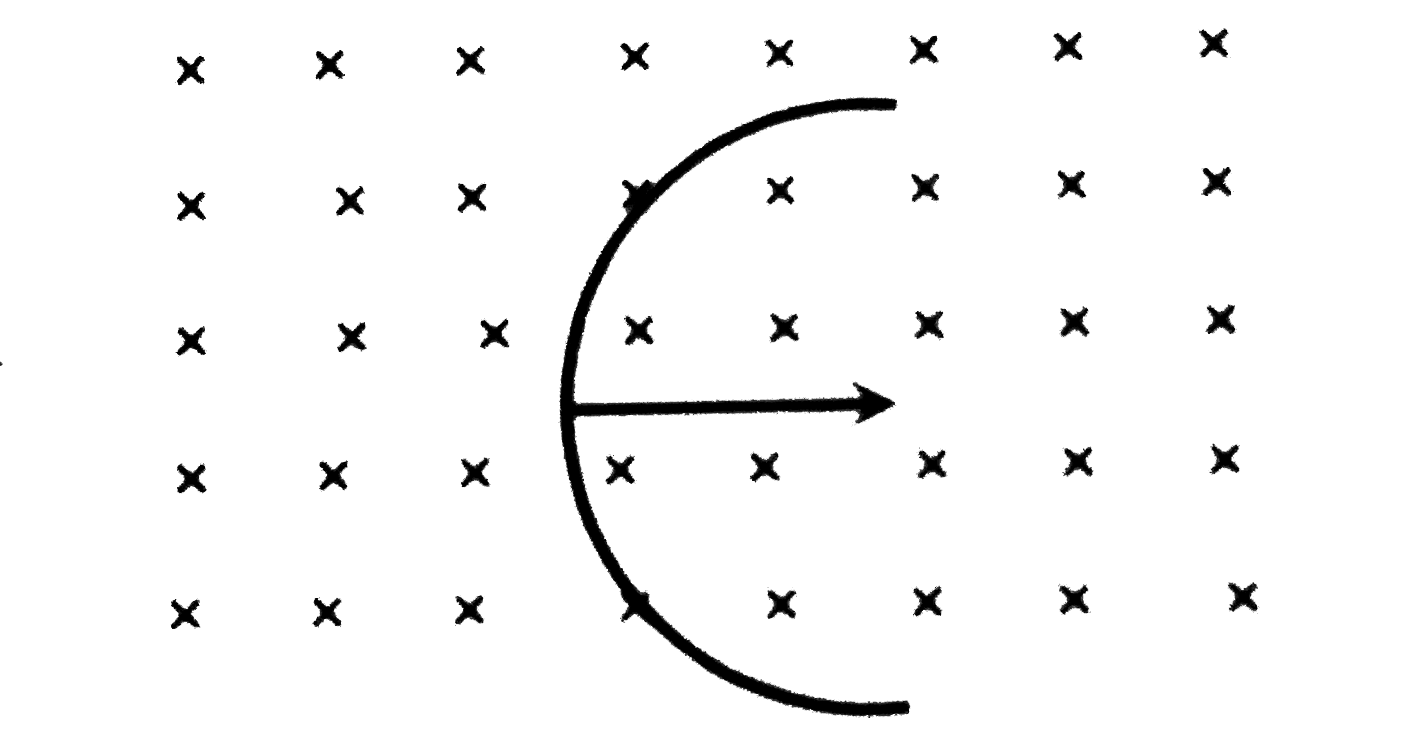 ABLvB2BKvC2πBLvD2BvLπ
ABLvB2BKvC2πBLvD2BvLπA conducting rod of length 2l is rotating with constant angular speed ω about is perpendicular bisector. A uniform magnetic field →B exists parallel to the axis of rotation. The e.m.f. induced between two ends of the rod is
 A12Bωl2B18Bωl2CZeroDBωl2
A12Bωl2B18Bωl2CZeroDBωl2A rod of length l is rotated with angular speed ω about an axis passing through the centre of rod and perpendicular to its length. A uniform magnetic field B is applied parallel to the axis of rotation, Potential difference developed between the ends of the rod is
ABlω22BBl(ω2)CBlω28DZero
A ring rotates with angular velocity ω about an axis perpendicular to the plane of the ring passing through the center of the ring.A constant magnetic field B exists parallel to the axis.Find the emf induced in the ring.

View SolutionA metallic rod of length lis hinged at one end and the other end is rotated with a constant angular speed ω about an axis passing through the hinge. A constant and uniform magnetic field B, parallel to the axis of rotation exists everywhere. The induced emf between the two ends of rod is 12Blω2.
View SolutionA ring rotates with angular velocity ω about an axis perpendicula to the plane of the ring passing through the center of the ring (Fig. 3.77). A constant magnetic field B exists parallel to the axis. Find the emf induced in the ring.

View SolutionA uniform rod of mass m is bent into the form of a semicircle of radius R. The moment of inertia of the rod about an axis passing through A and perpendicular to the plane of the paper is

View Solutiona semicircle wire of radius R is rotated with constant angular velocity about an axis passing through one end and perpendicular to the plane of wire. There is a uniform magnetic field of strength B. The induced emf between the ends is

View Solution
