Two parallel vertical metellic rails AB and CD are separated by 1m. They are connecting at two ends by resistances R1 and R2 as shown in Fig. 3.96. A horizontal metallic bar L mas 0.2kg slides without friction vertically down the rails under the action of gravity. There is a uniform horozontal magnetic field of 0.6T perpendicular to the plane of the rails. It is observed that when the terminal velocity is attained, thwe power dissipated in R1andR2 are 0.76and1.2W, respectively. Find the terminal velocity of the bar L and the values of R1andR2.

Let magnetic field B=0.6T be inward as shown Fig. 3.97. When the rod moves down due to gravity, emf is induced in the rod as shown. Due to this, current I flows in the rod which results in force F on the rod in upward direction. Let at any instant of time, velocity of rod be v.
Then e=BvlandI=eReq,
where 1Req=1R1+1R2
F=IlB=eReqlB=B2l2vReq
Initially, F is less than mg. But as the velocity increases, F also increases. At a certain time, F will be equal to mg. At that time net force on the rod will become zero and velocity of rod will velocity. Let it be vt. So putting F=mg
→ B2l2vtReq=mg ltbr> But at this time, power disspated in resistances is
P1+P2=0.76+1.2=1.96W
So we have e2Req=P1+P2 → B2l2v2tReq=1.96 ltbr> From Eqs. (i) and (ii) vt=1.96mg=1.960.2×9.8=1ms−1
From Eqs. (i) and Req=B2l2vtmg=(0.6)2×12×10.2×9.8=949Ω
P1P2=e2/R1e2/R2 → 0.761.20=R2R1 → 1930=R2R1
1Req=1R1+1R2 → 499=1R1+3019R1
→ R1=919Ω and R2=1930R1=1930×919=0.3Ω
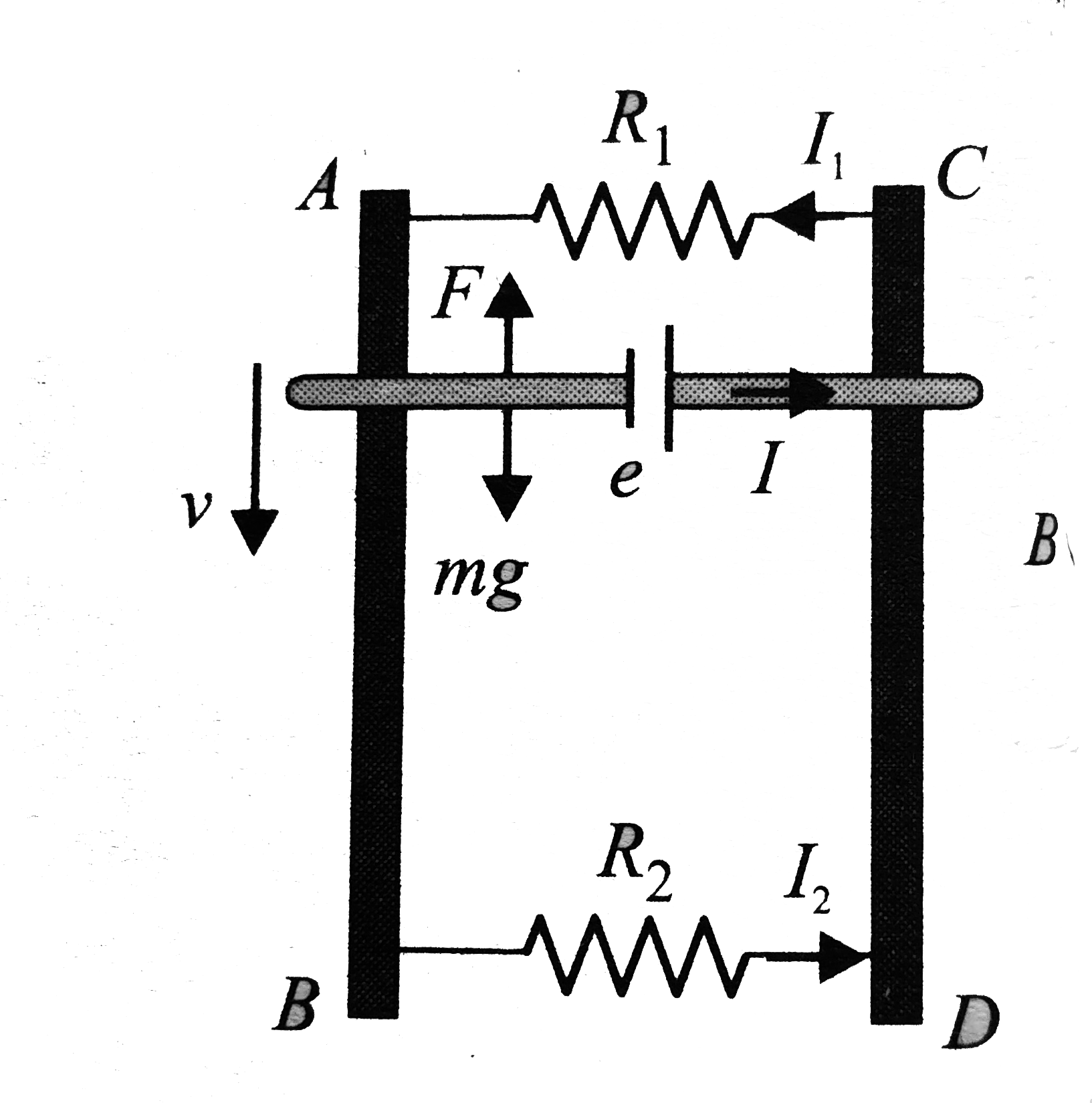
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 3.1
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 3.2
27 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - compression type
7 Videos
- ELECTROMAGENTIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGENTIC INDUCTIONEXERCISE - QUESTION BANK
40 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
Two parallel vertical metallic rails AB and CD are separated by 1m. They are connected at two ends by resistanace (R1)and(R2) as shown in fig. A horizontal metallic bar L of mass 0.2 kg slides without froction vertically down the rails under the action of gravity. THere is a uniform horizontal magnetic field of 0.6 Tesla perpendicular to the plane of the rails. It is observed taht when the teminal velocity is attained, the power dissipated in (R1)and(R2) are 0.6 watt and 1.2 watt respectively. Find the terminal velocity of the bar L and the values of (R1)and(R2).
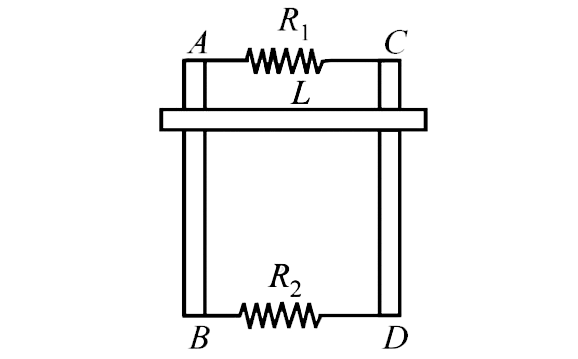
View SolutionTwo parallel vertivcal inetallic ralis AB and CD are serparated by l= 1 m . They are connected at the ends by resistance R1 and R2 as show in the figure . A horizationl metallic bar L of mass m= 0.2 kg slides without friction vertically down the rails under the action of gravity . These is a unifrom horizonal magnetic field of a B=0.6T perpendicular to the plane to rails . It is observed that when the termainal veloctity is attained , the power disspated in R1 and R2 are P1=0.76W and P2=1.2W respectively . Find the terminal velocity of bar L and the values of R1 and R2
View Solution
Knowledge Check
Two parallel vertical metallic rails AB and CD are separated by 1m. They are connected at the two ends by resistances R1 and R2 as shown in the figure. A horizontal metallic bar l of mass 0.2kg slides without friction, vertically down the rails under the action of gravity. There is a uniform horizontal magnetic field of 0.6T perpendicular to the plane of the rails. It is observed that when the terminal velocity is attained, the powers dissipated in R1 and R2 are 0.76W and 1.2W respectively (g=9.8m/s2)
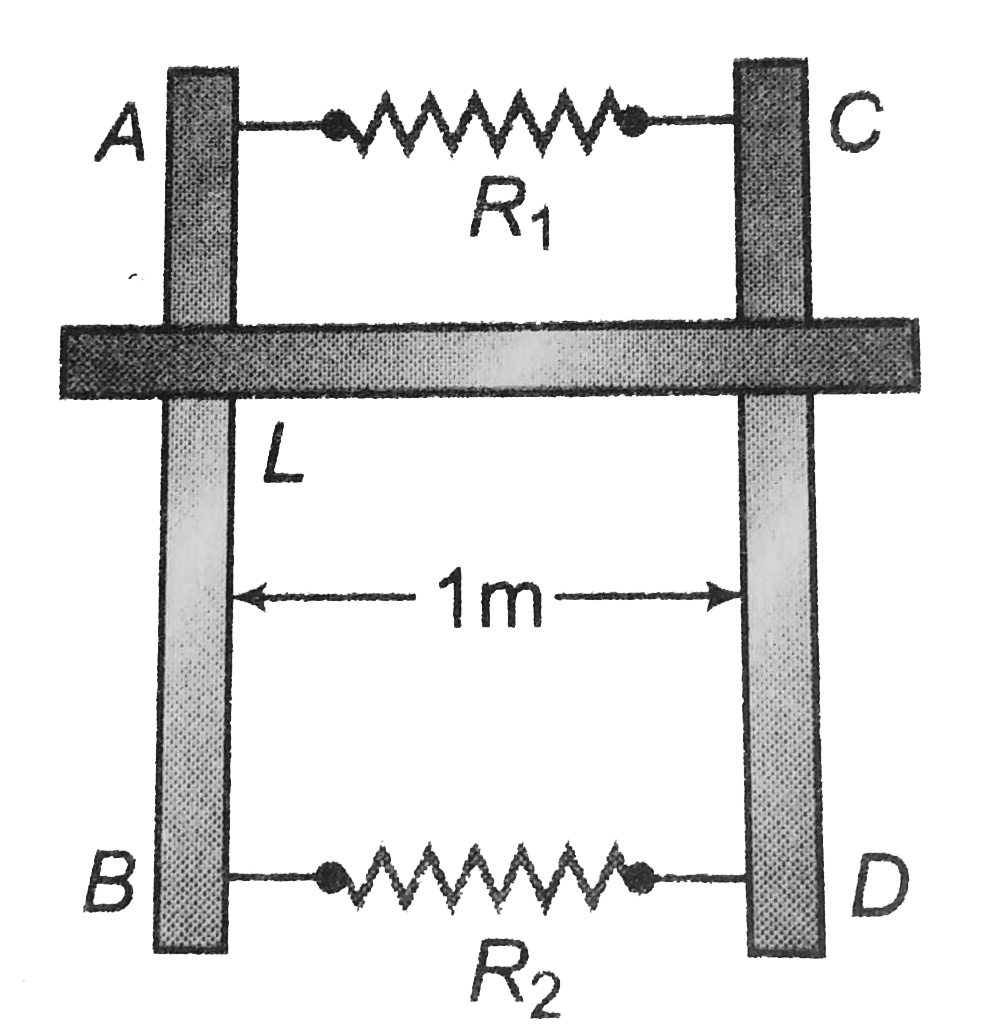
The terminal velocity fo the bar L will beA2m/sB3m/sC1m/sDNone of theseTwo parallel vertical metallic rails AB and CD are separated by 1m. They are connected at the two ends by resistances R1 and R2 as shown in the figure. A horizontal metallic bar l of mass 0.2kg slides without friction, vertically down the rails under the action of gravity. There is a uniform horizontal magnetic field of 0.6T perpendicular to the plane of the rails. It is observed that when the terminal velocity is attained, the powers dissipated in R1 and R2 are 0.76W and 1.2W respectively (g=9.8m/s2)
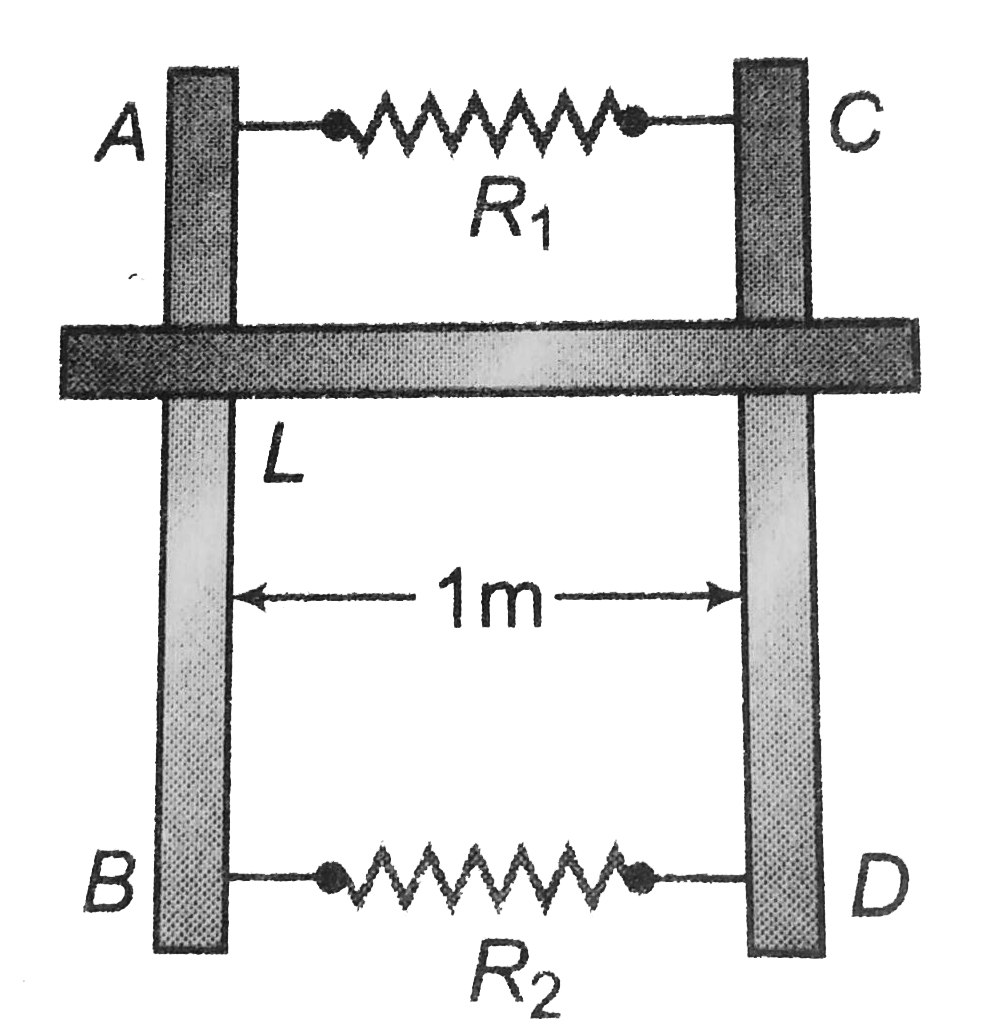
The value of R1 isA0.47ΩB0.82ΩC0.12ΩDNone of theseTwo parallel vertical metallic rails AB and CD are separated by 1m. They are connected at the two ends by resistances R1 and R2 as shown in the figure. A horizontal metallic bar l of mass 0.2kg slides without friction, vertically down the rails under the action of gravity. There is a uniform horizontal magnetic field of 0.6T perpendicular to the plane of the rails. It is observed that when the terminal velocity is attained, the powers dissipated in R1 and R2 are 0.76W and 1.2W respectively (g=9.8m/s2)
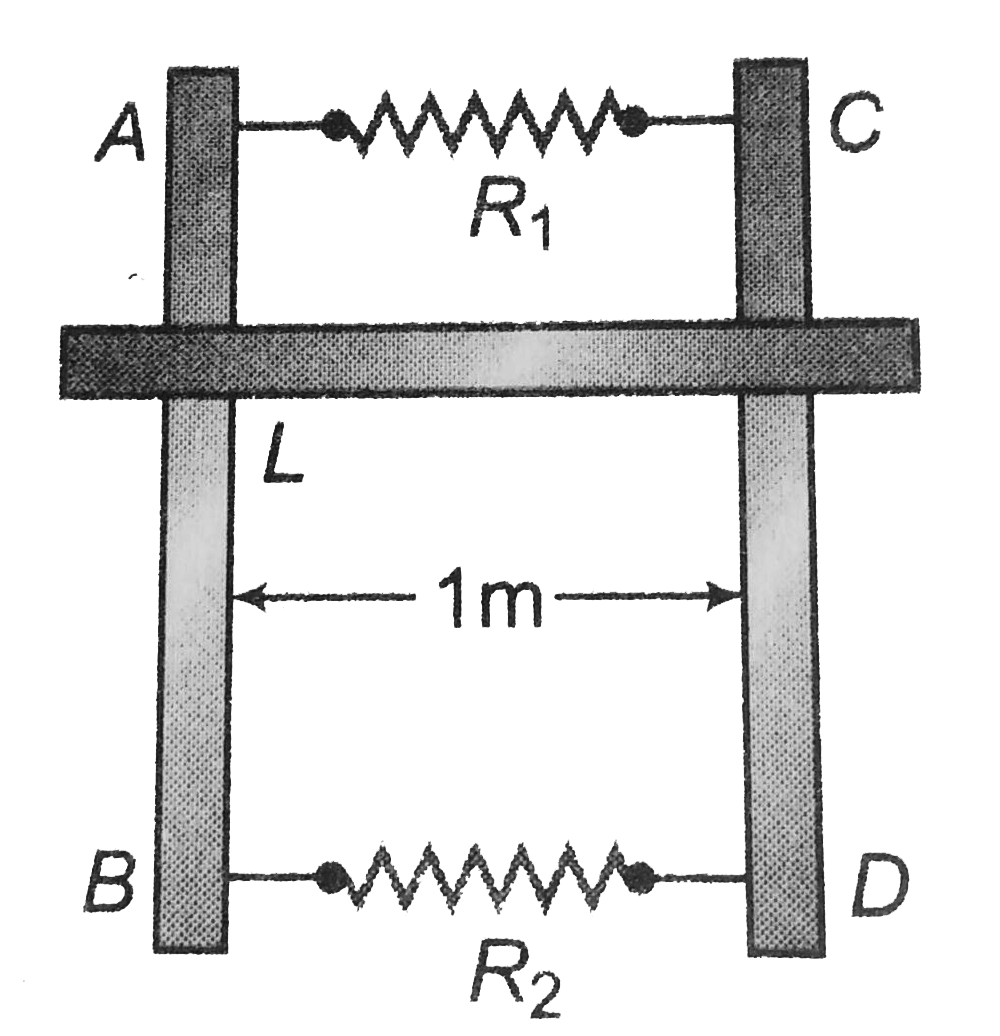
The value of R2isA0.6ΩB0.5ΩC0.4ΩD0.3Ω
Two parallel vertical metallic bars XX1 and YY1, of negligible resistance and separated by a length 'l', are as shown in Fig. The ends of the bars are joined by resistance R1 and R2. A uniform magnetic field of induction B exsits in space normal to the plane of the bars. A horizontal metallic rod PQ of mass m starts falling vertically, making contact with the bars. It is oberved that in the steady state the powers dissipated in the resistance R1 and R2 and the terminal velocity attained by the rod PQ.
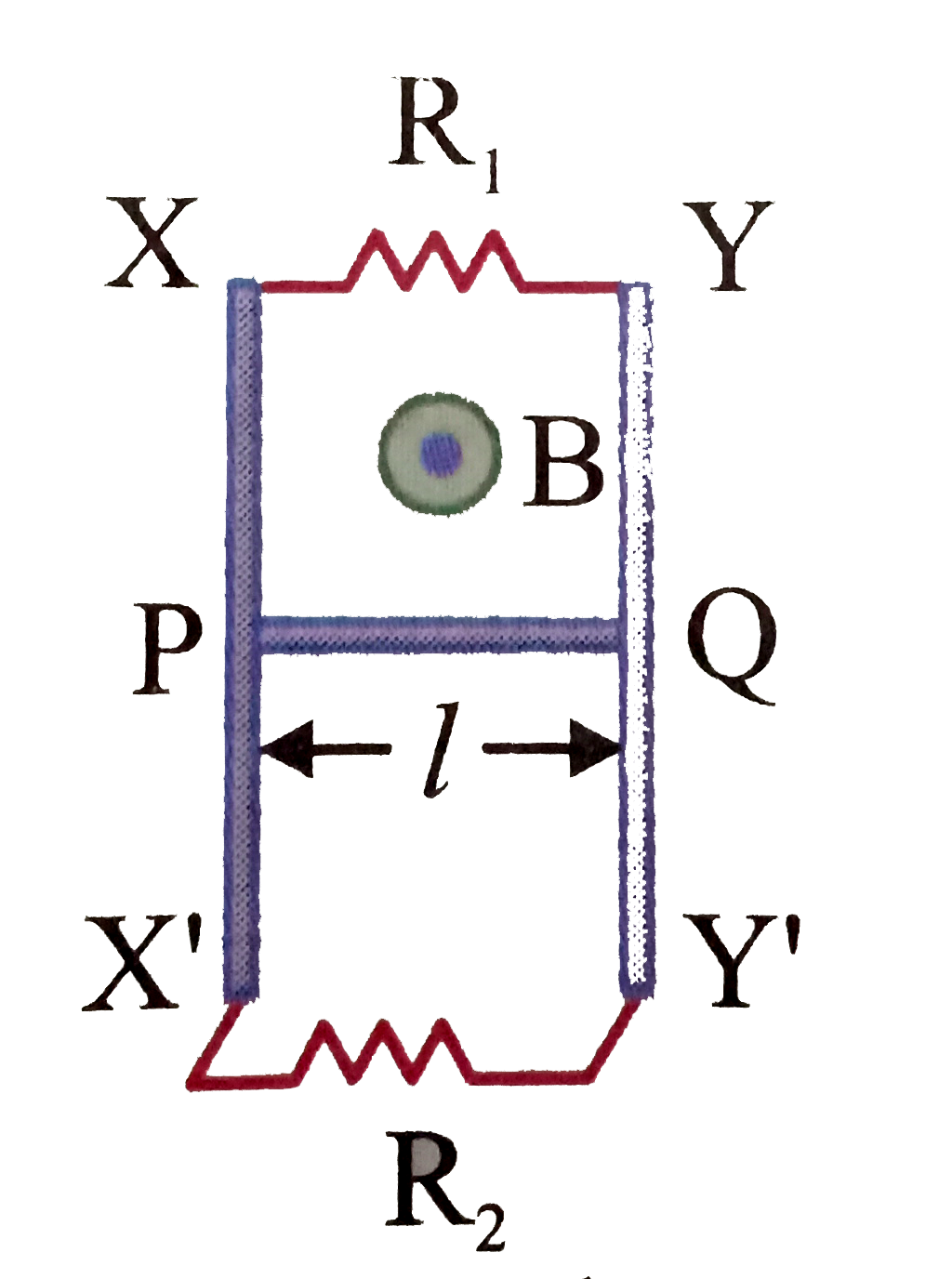
View SolutionA copper bar of mass m sides under gravity on two smooth parallel rails l distance apart and set at angle α to the horizontal . At the lop , the rails are joined by a resistor R. Calculate the steady velocity of the bar the n when there is a unifrom magnetic field B perpedicular to the plane of the rails .
View SolutionA conducting wire xy of lentgh l and mass m is sliding without friction on vertical conduction rails ab and cd as shown in figure. A uniform magnetic field B exists perpendicular to the plane of the rails, x moves with a constant velocity of

View SolutionA copper rod of mass m slides under gravity on two smooth parallel rails l distance apart set at an angle θ to the horizontal. At the bottom, the rails are joined by a resistance R.

There is a uniform magnetic field perpendicular to the plane of the rails. the terminal valocity of the rod is
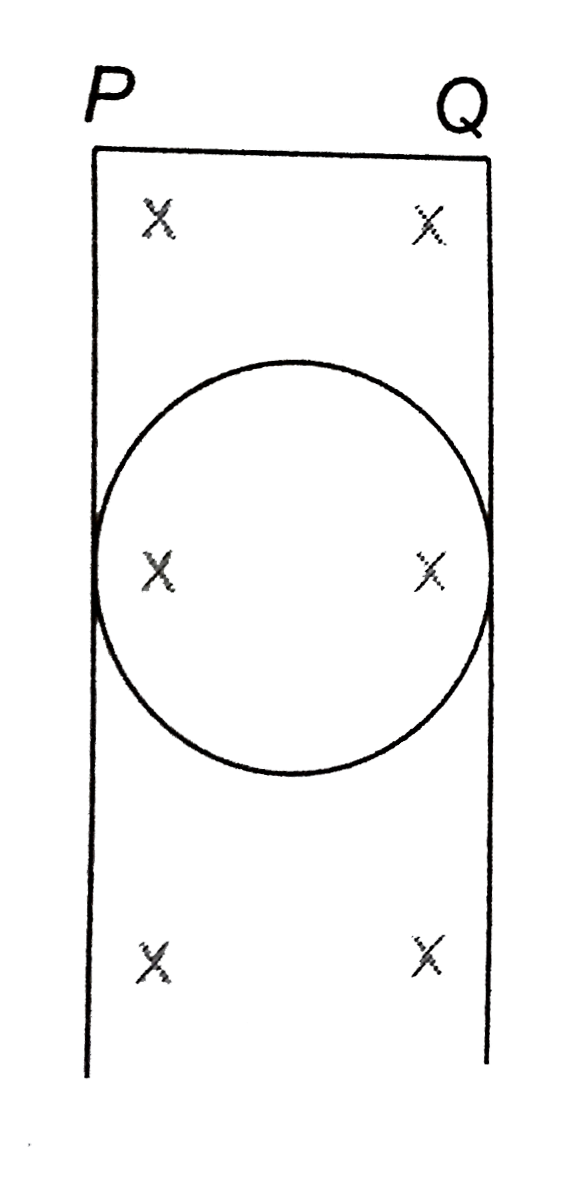
View SolutionA vertical ring of radius r and resistance on R falls vertically. It is in contact with two vertical rails which are joined at the top. The rails are without friction and resistance. There is a horizontal uniform, magnetic field of magnitude B perpendicular to the plane of the ring and the rails. When the speed of the ring is v , the current in the section PQ is
View Solution
