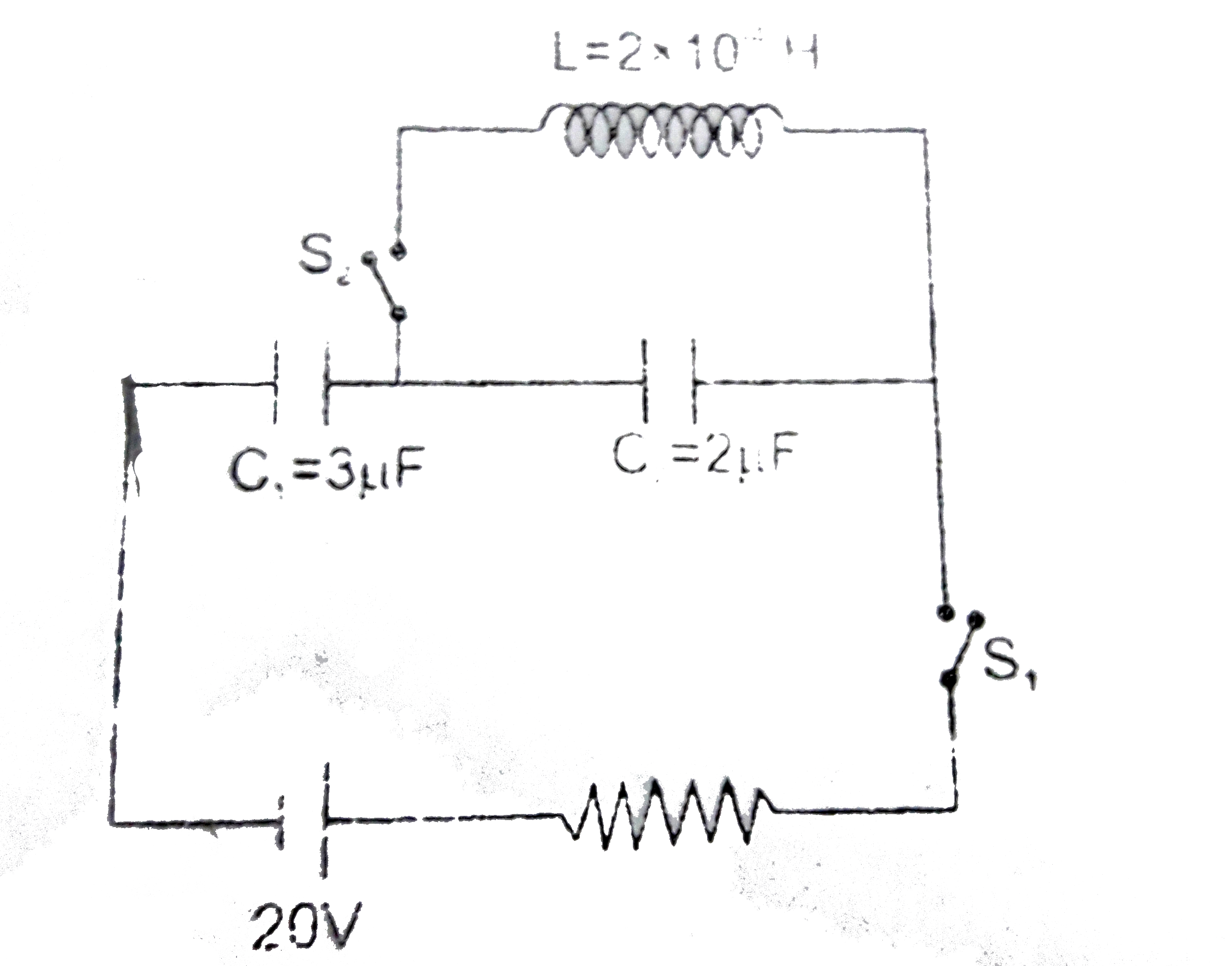
The circuit shows in Fig. is in the steady state with switch S1 closed. At t=0,S1 is opened and switch S2 is closed.
a. Derive expression for the charge on capacitor C2 as a function of time.
b. Determine the first instant t, when the energy in the inductor becomes one-third of that in the capacitor.

In the steady state, C1 and C2 are in series arrangement, their equivalent is
Ceq=C1C2C1+C2=1.2μF
Charge on the capacitor C2,Q0=CeqV=1.2×20=24μC.
When S1 is opened, S2 is closed. Capacitor C2 starts discharging through the inductor and let at any time t, charge on the capacitor be Q. Then we know that
Q=Q0cosωt
UE+UB=Q202C2
where ω=1√LC2=1√0.2×10−3×2×10−6=50,000rads−1
At the times t=t1,UB=13UE, but UB+UE=Q202C2
Hence, UE=34(12Q20C2)⇒12Q2C2=34(12Q20C2)
Q=√32Q0 or Q0cosωt1=√32Q0
ωt1 or t1=π6ω=1.05×10−5=10.5μs
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Solved Examples
3 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercise 4.1
24 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
28 Videos
- KINETIC THEORYBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORYEXERCISE - Question Bank
31 Videos
Similar Questions
The circuit shown in figure is in the steady state with switch S1 closed. At t=0, S1 is opened and switch S2 is closed.
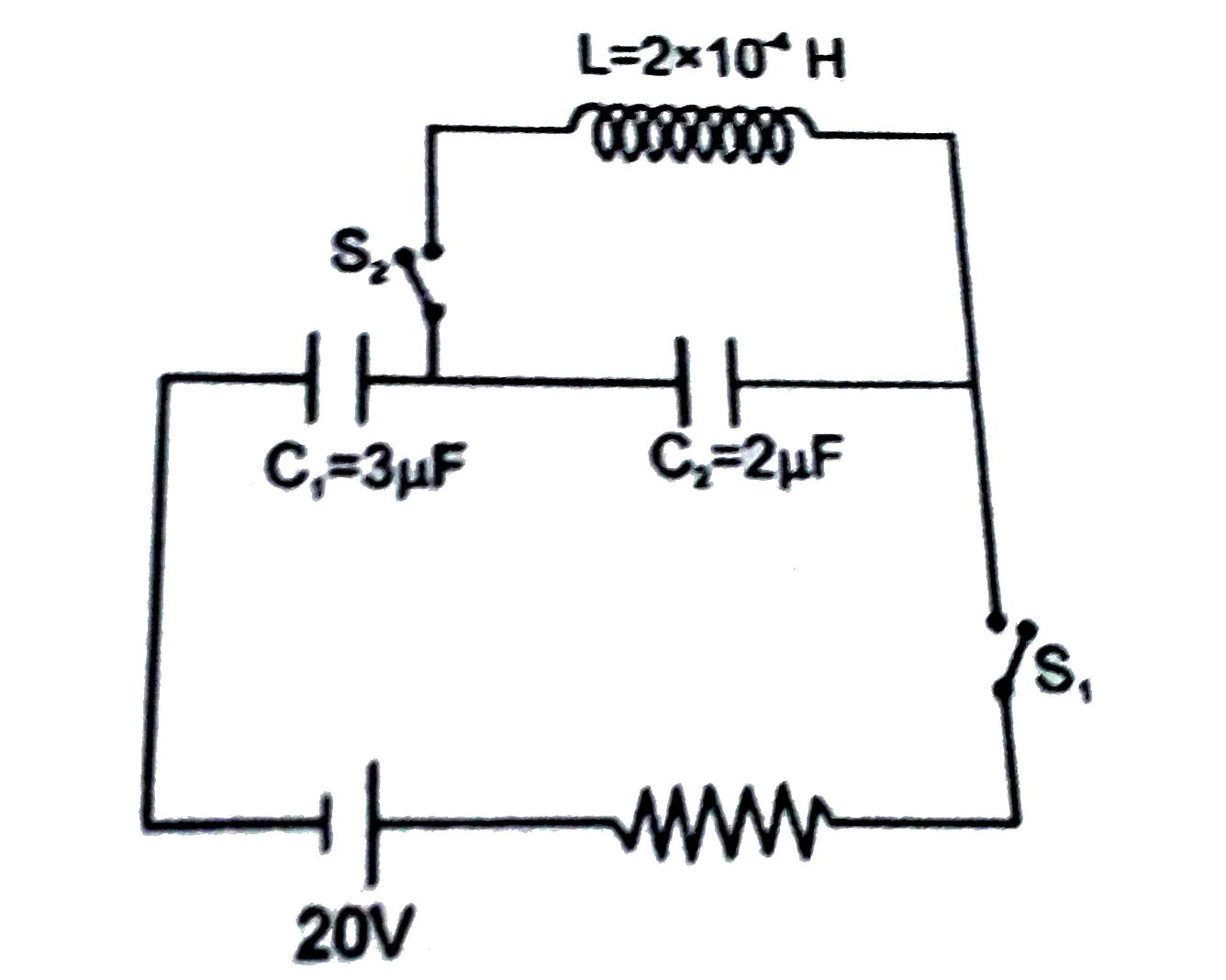
Find the first instant t, when energy in inductor becomes one third of that in capacitor
View SolutionA circuit containing capacitors C1 and C2, shown in the figure is in the steady state with key K1 and K2 opened. At the instant t=0, K1 is opened and K2 is closed.
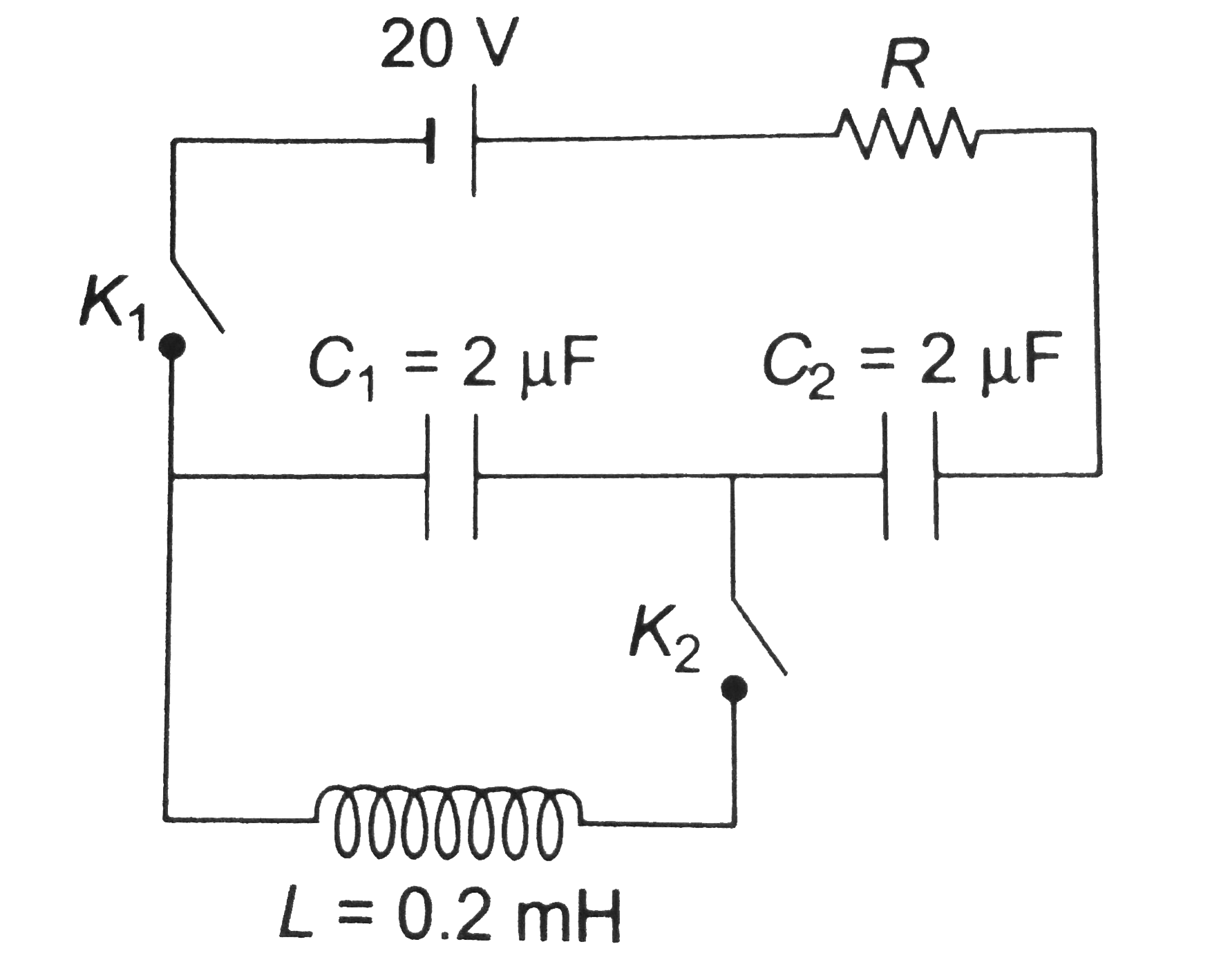
(a) Find the angular frequency of oscillations of L−C circuit.
(b) Determine the first instant t, when energy in the inductor becomes one third of that in the capacitor.
(c) Calculate the charge on the plates of the capacitor at that instant.
View Solution
Knowledge Check
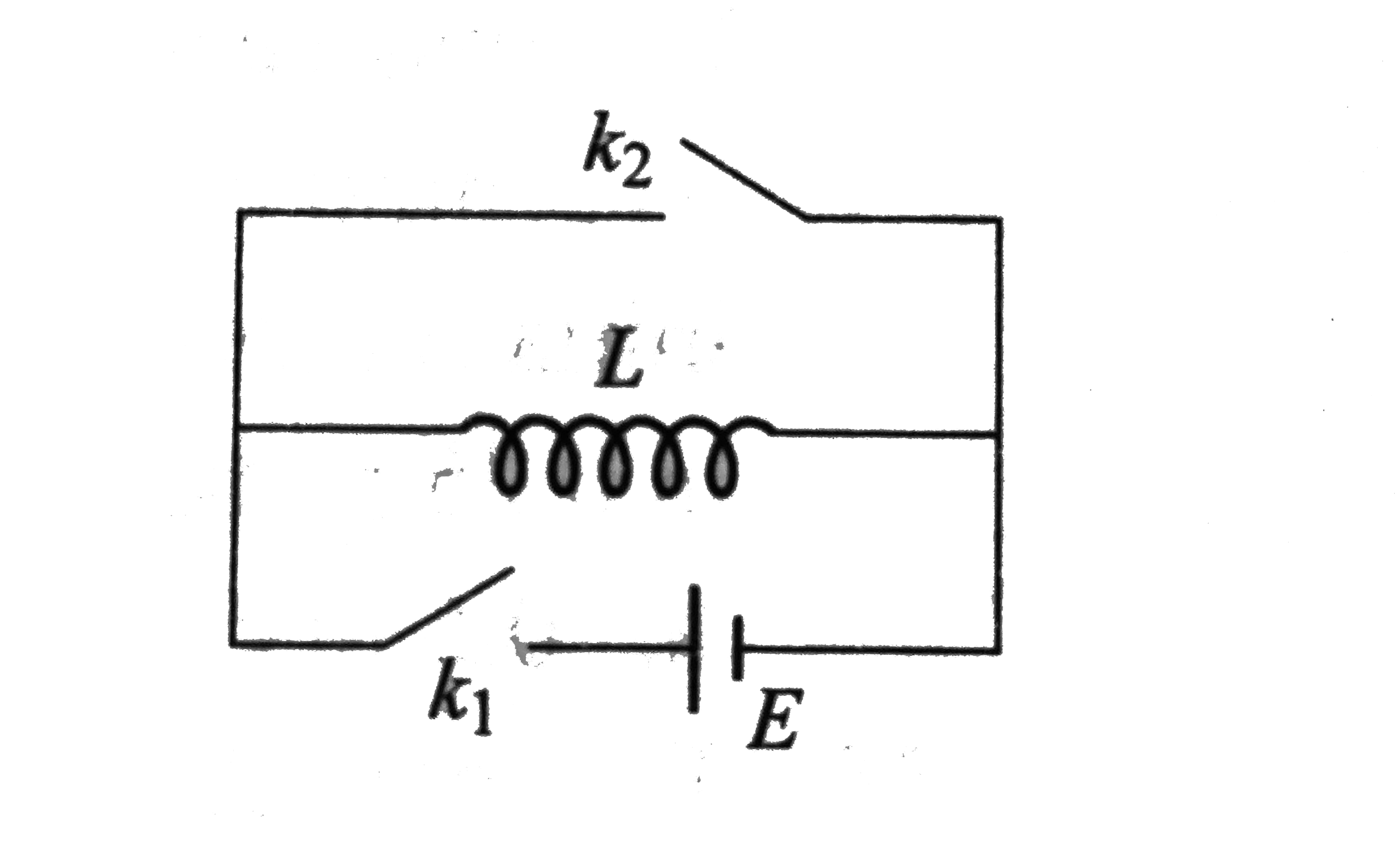
In the circuit shows in Fig. switch k2 is open and switch k1 is closed at t=0. At time t=t0, switch k1 is opened and switch k2 is simultaneosuly closed. The variation of inductor current with time is
 A
A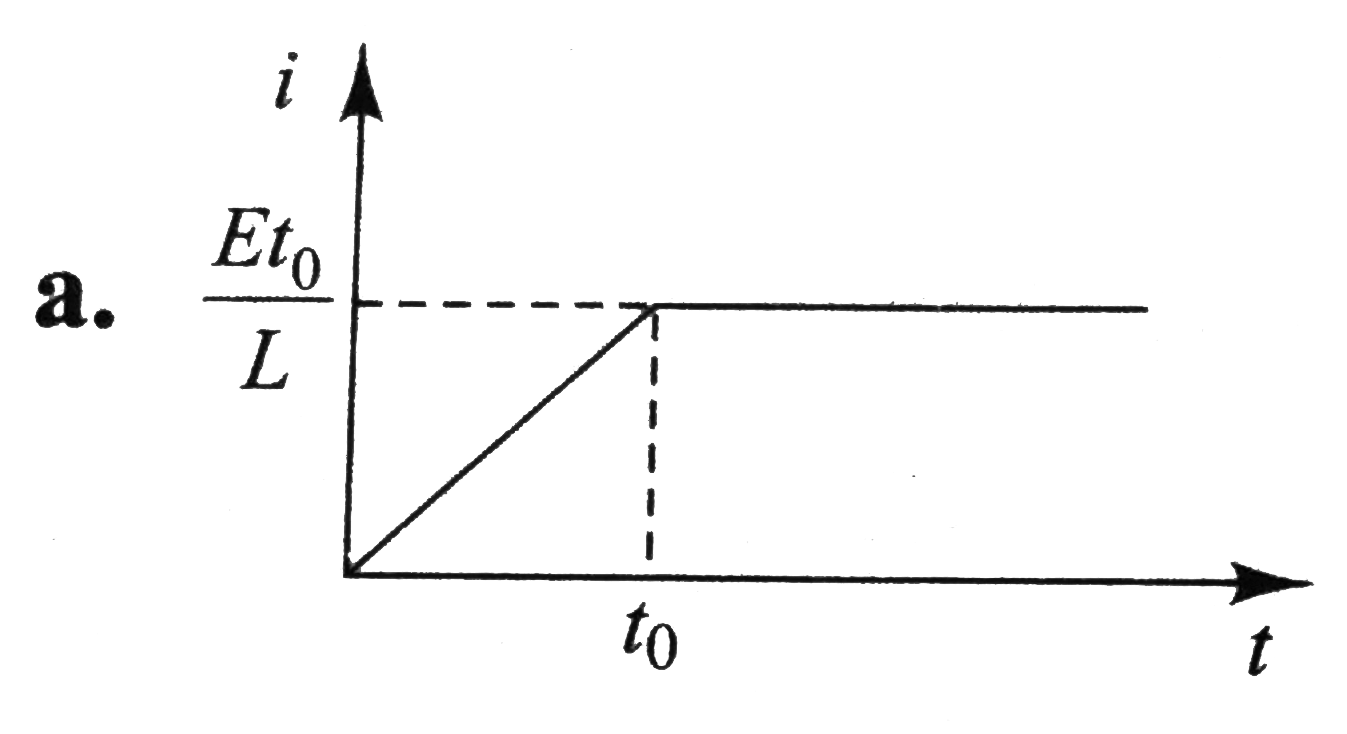 B
B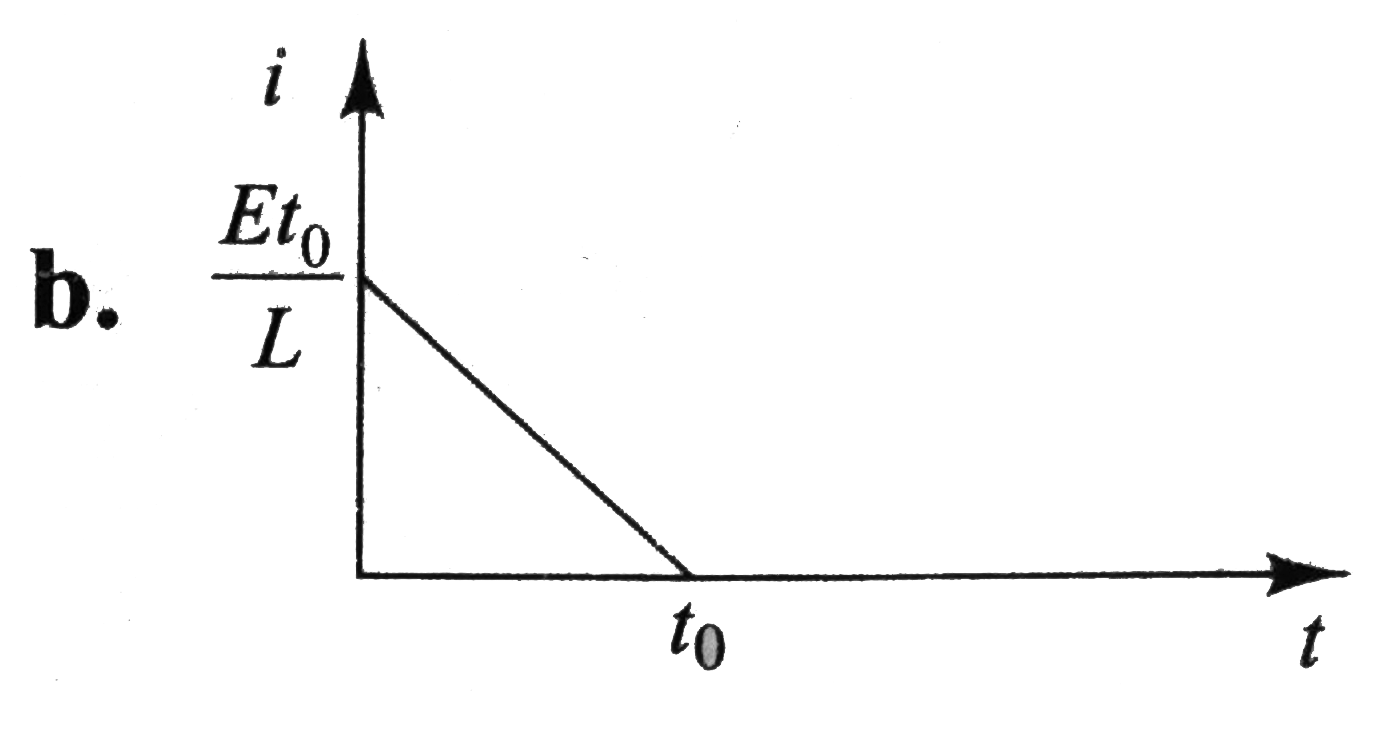 C
C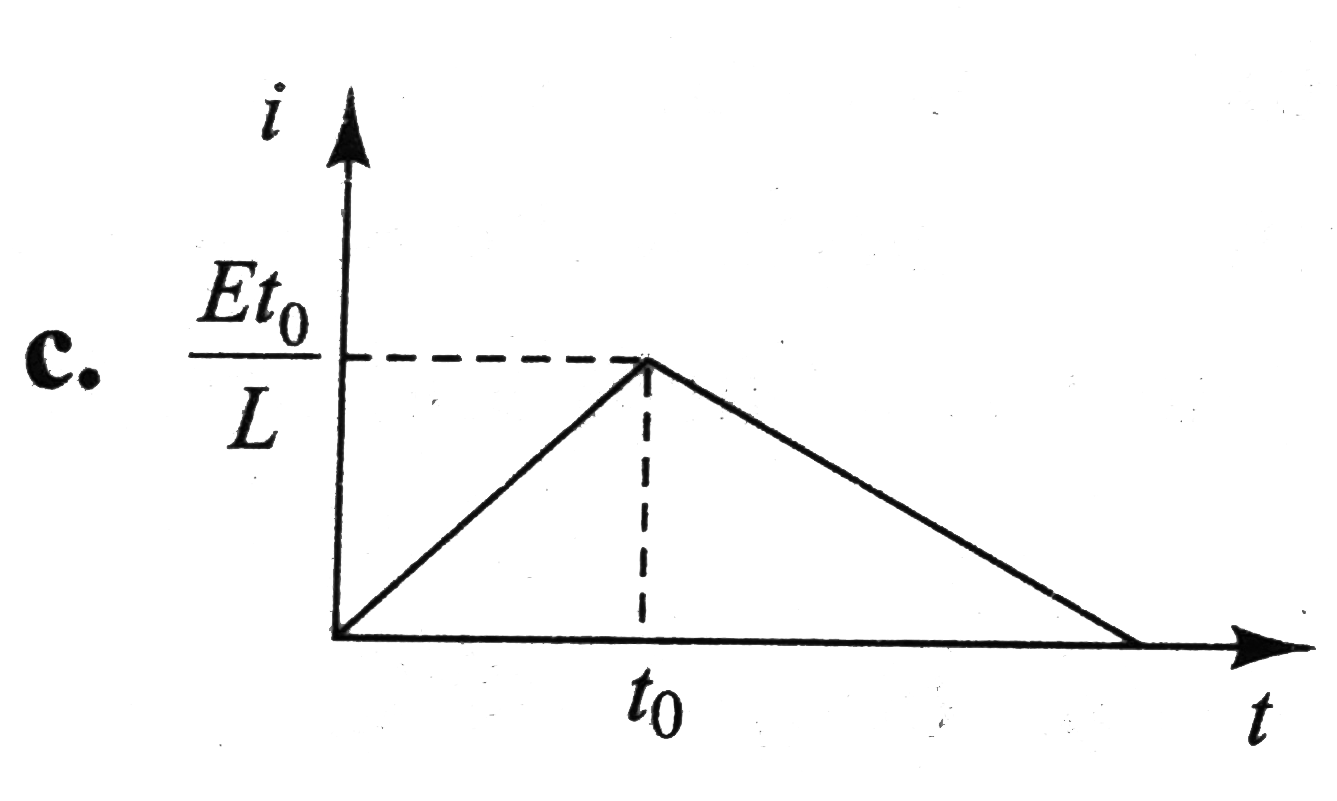 D
D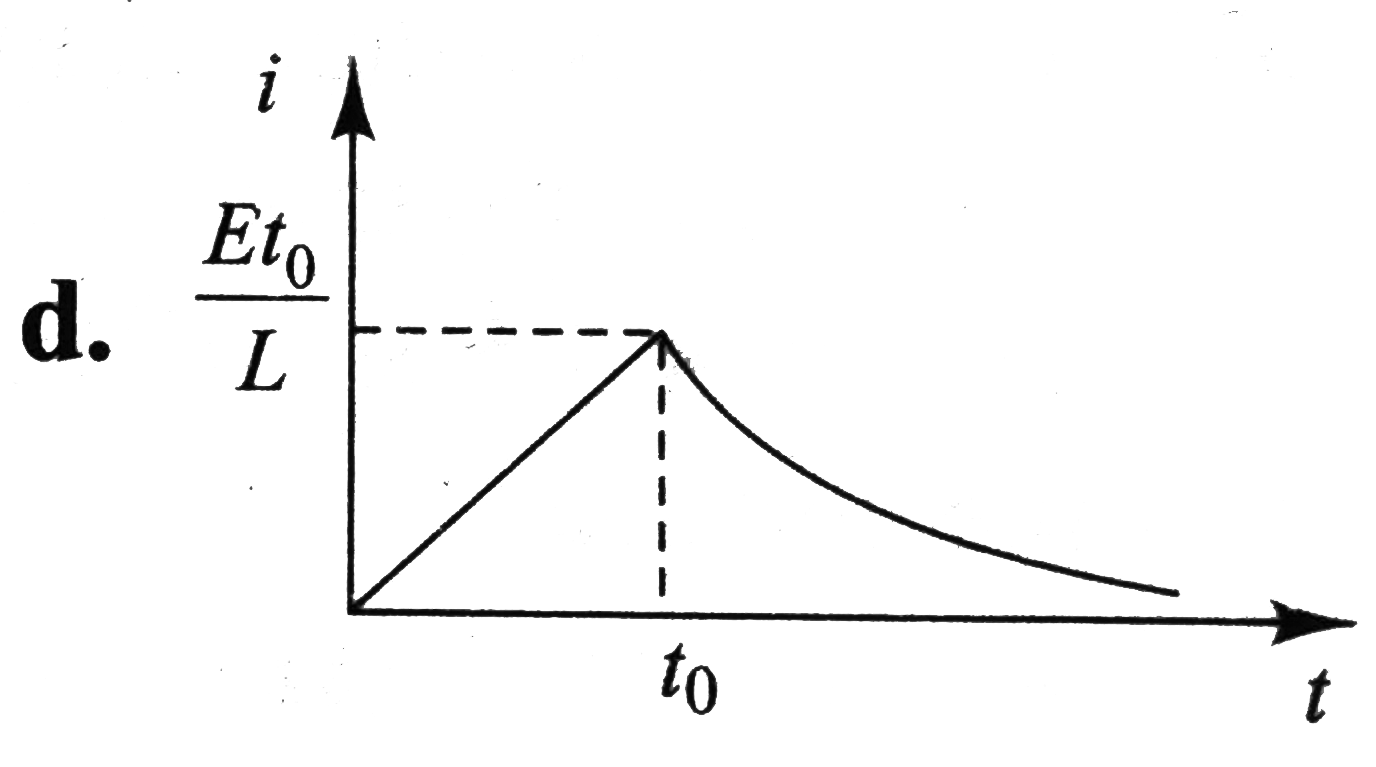
In the circuit shown in, C1=6μF,C2=3μF, and battery B=20V. The switch S1 is first closed. It is then opened, and S2 is closed. What is the final charge on C2
 . A120μCB80μCC40μCD20μC
. A120μCB80μCC40μCD20μC
The circuit shown in figure is in the steady state with switch S1 closed.At t=0,S1 is opened and switch S2 is closed. The first instant t when energy in inductor becomes one third of that in capacitor is equal to π×10−5xsec. Then finout value of x.
View SolutionFigure-5.150 shows LC circuit with initial charge on capacitor 200μC. If at t=0 switch is closed, find the first instant when energy stored in inductor becomes one third that of capacitor.

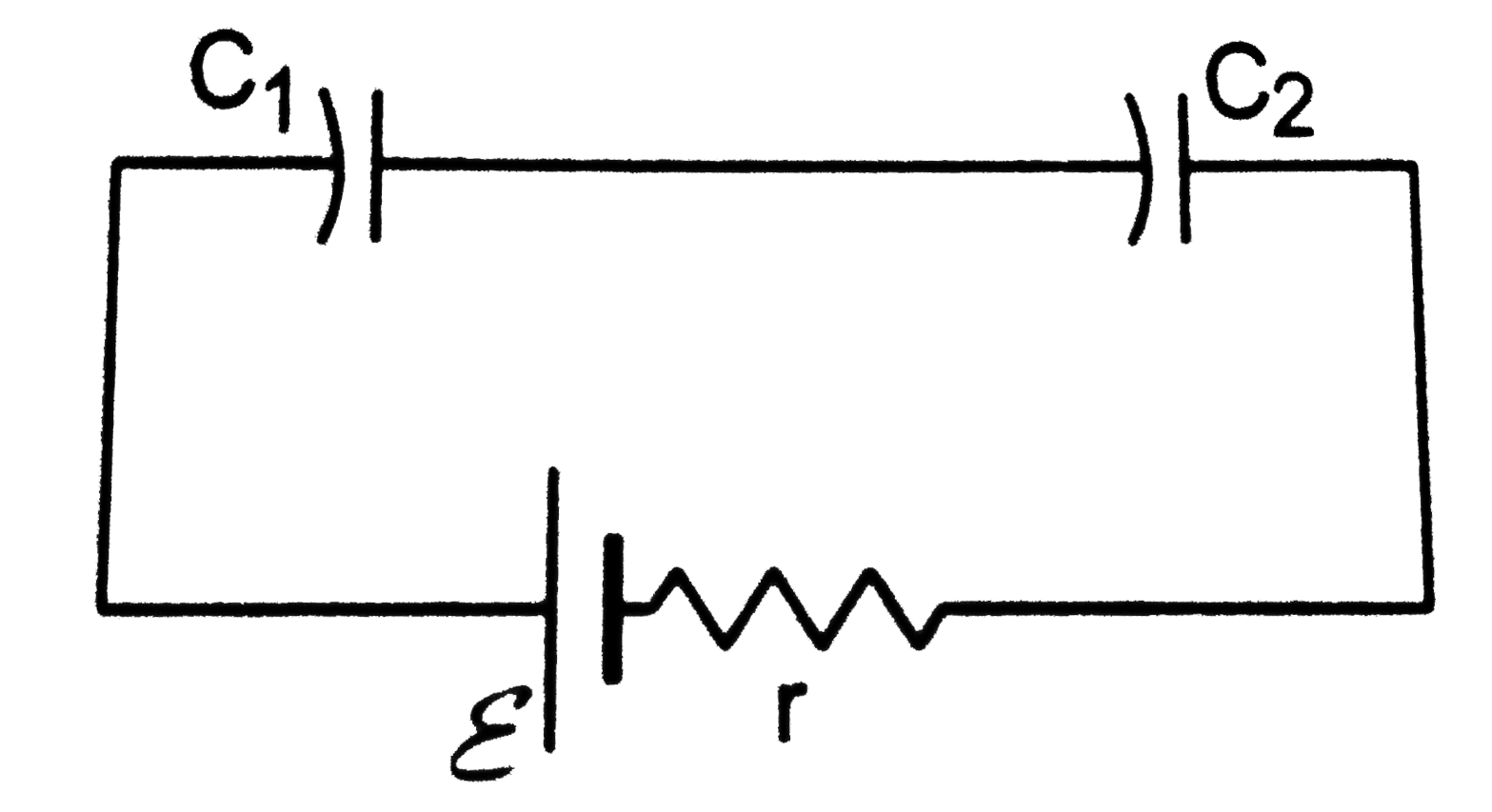
View SolutionConsider the situation shown in figure.The switch is closed at t=0when the capacitor C1as a function of time t.
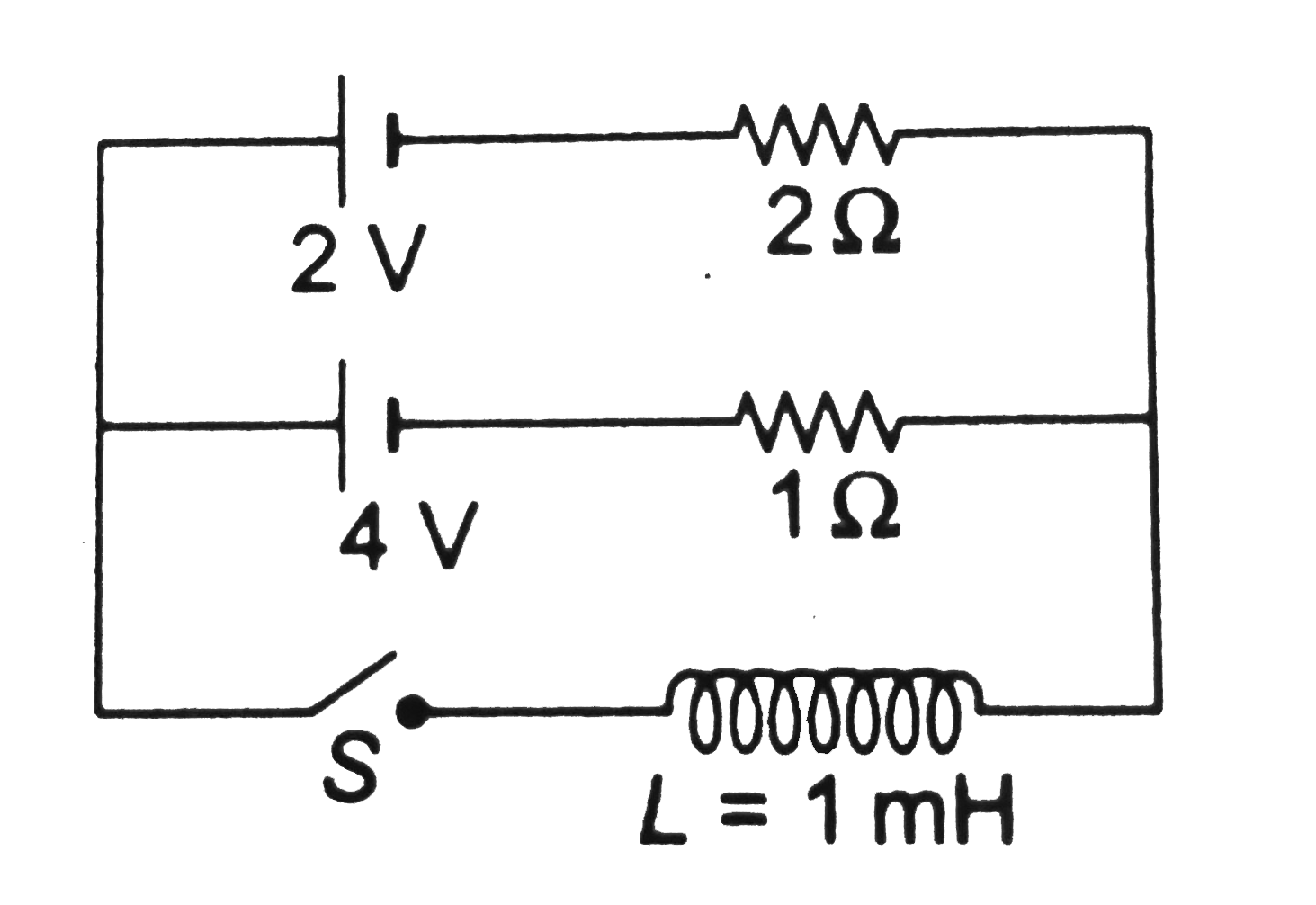
View SolutionIn the circuit shown, switch S is closed at time t=0. Find the current through the inductor as a function of time t.
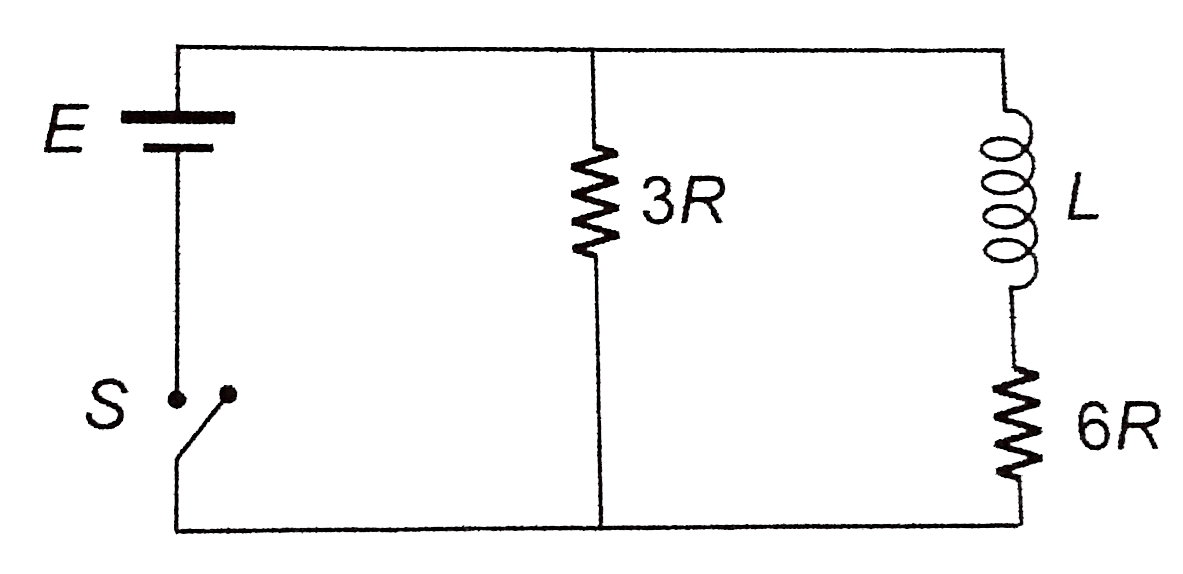
View SolutionAt t=0 , switch S is closed. Find time constant of the circuit and current through inductor as a function of time t .

View SolutionIn the circult shown
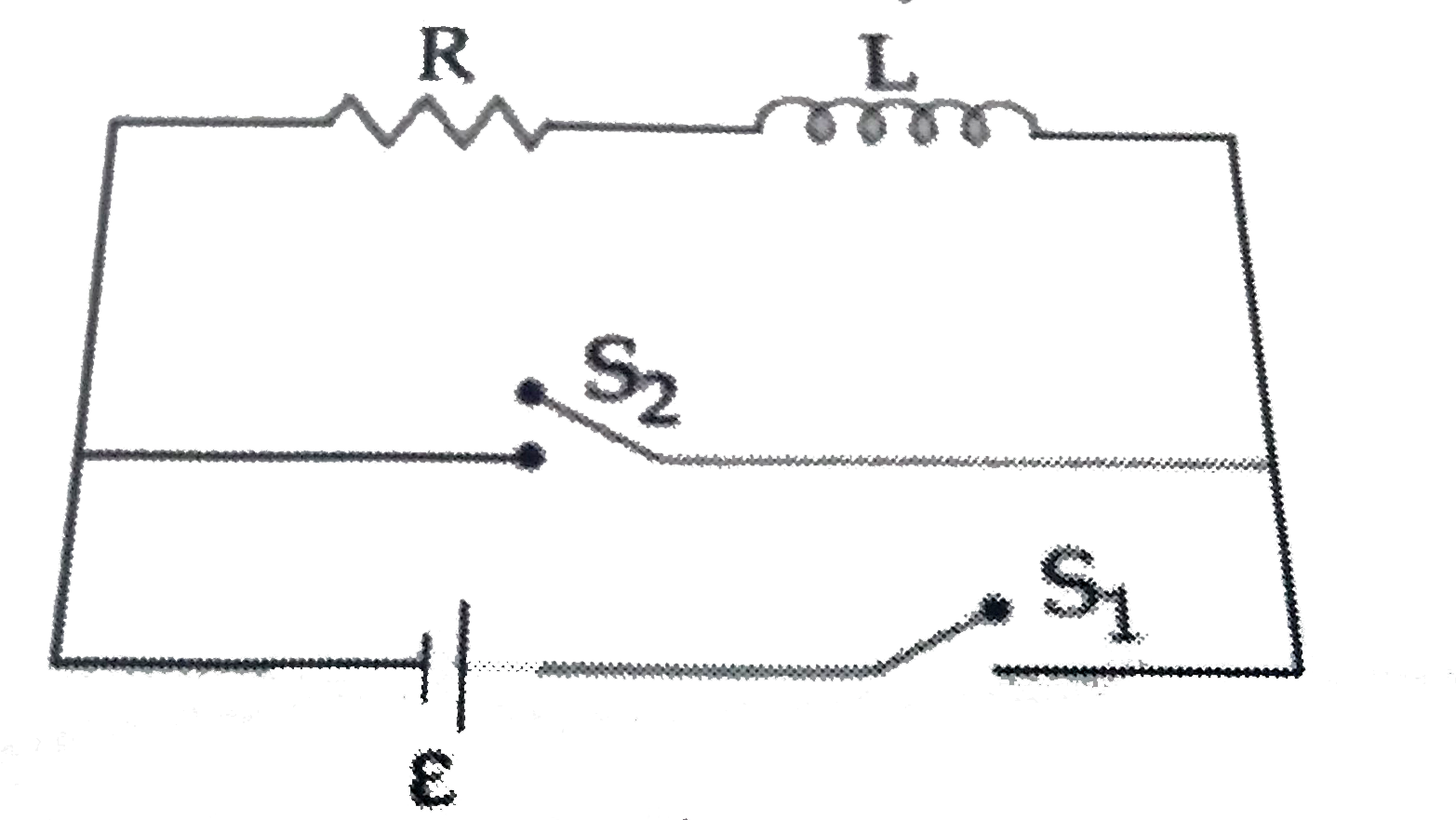 the switch S1 is closed at time t=0 and the swith S2 is kept open. At some later time (t0) ,the swith S1 is opened and S2 is closed .The behaviour of the current I as a function of time 't' is given by :
the switch S1 is closed at time t=0 and the swith S2 is kept open. At some later time (t0) ,the swith S1 is opened and S2 is closed .The behaviour of the current I as a function of time 't' is given by :
View Solution
