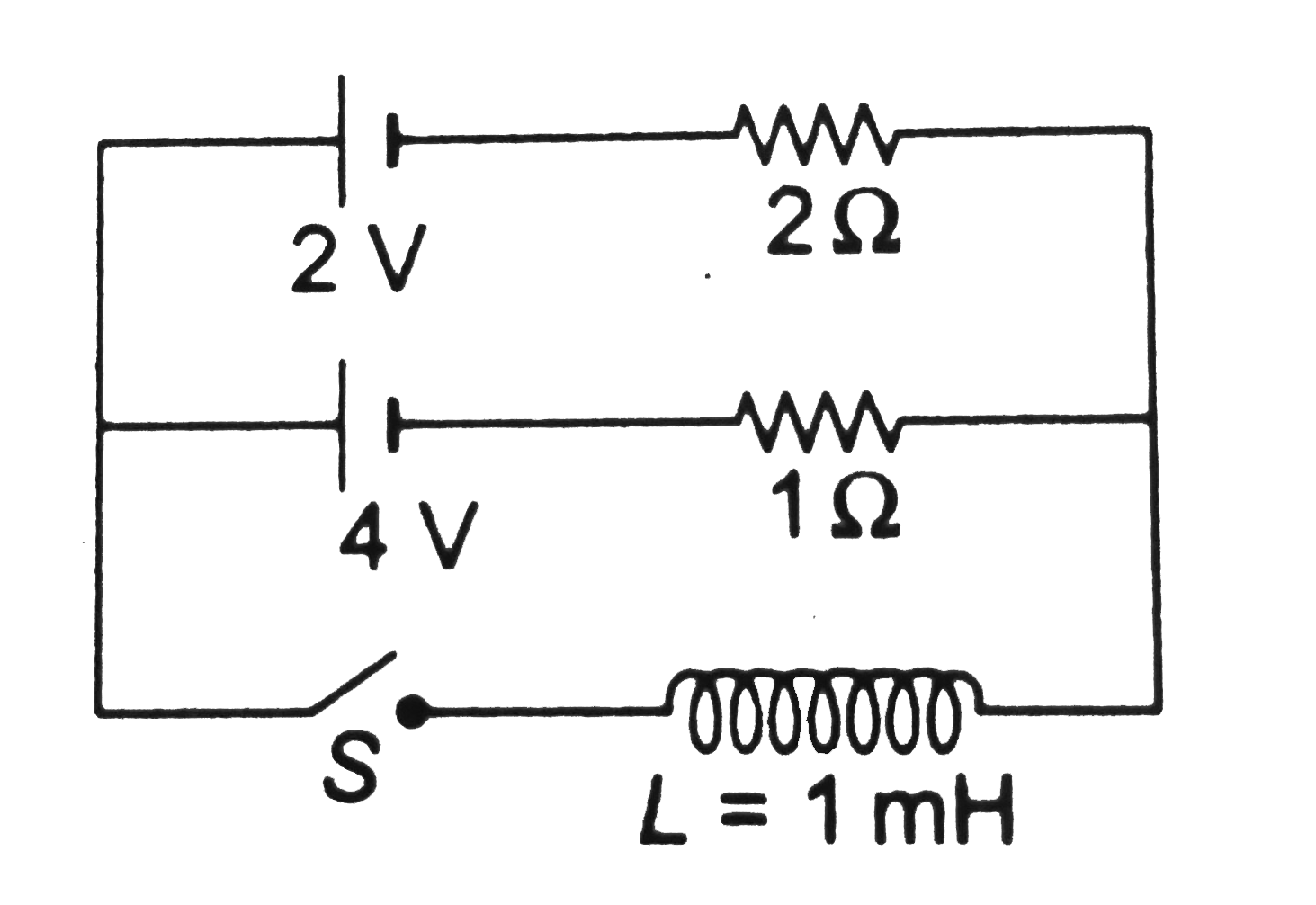
In the circuit shows in Fig the capacitor is initially uncharged and the two - way switch is connected in the position BC. Find the current through the resistence R as a function of time t. After time t=4 ms, the switch is connected in the position AC. Find the frequency of oscillation of the capacitor of the circuit in the position, and the maximum charge on the capacitor C. At what time will the energy stored in the capacitor be one-half of the total energy stored in the circuit? It is given L=2×10−4H,C=5mF,R=In210Ω and emf of the battery =1V.
Text Solution
The correct Answer is:10In2⎛⎝1−(12)t2×10−3⎞⎠;103rads−1;7.5×10−3In2C;
4ms+nπ+(−1)nπ/4ω
Current in R or L at any time is given by:
I=ɛR(1−e−Rt/L)⇒I=1(In2)/10[1−e−tIn210×2×10−4]
⇒I=10In2⎡⎣1−eIn2−(t2×10−3)⎤⎦⇒I=10In2⎡⎣1−(12)t2×10−3⎤⎦
Now at t=4ms
I=10In2⎡⎢⎣1−(12)4×10−32×10−3⎤⎥⎦=10In2[1−14]=152In2A
Now the switch is shifted between A and C. Just after shifting the switch, current in inductor will be as calculated above. It can't change at once. Now due to this current, the capacitor will start charging. Frequency of oscillation is given by :
ω=1√LC=1√2×10−4×5×10−3=103rad/s
To find maximum charge : Q22C=12LI2
⇒Q=(√LC)I=10−3×152In2⇒Q=7.5×10−3In2C
Energy in the capacitor is half of total energy when charge on
capacitor is q=Q√2
Charge on capacitor at any time
q=Qsinωt[∵att=0,q=0]
⇒Q√2=Qsinωt⇒ωt=nπ+(−1)nπ4
(1) ⇒t=nπ+(−1)nπ/4ω
Total time, T=4ms+nπ+(−1)nπ/4ω
|
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercises (single Correct )
65 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercises (multiple Correct )
7 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercise 4.1
24 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
28 Videos
- KINETIC THEORYBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORYEXERCISE - Question Bank
31 Videos
Similar Questions
Knowledge Check
In the circuit shown in figure, the capacitors are initially uncharged. The current through resistor PQ just after closing the switch is
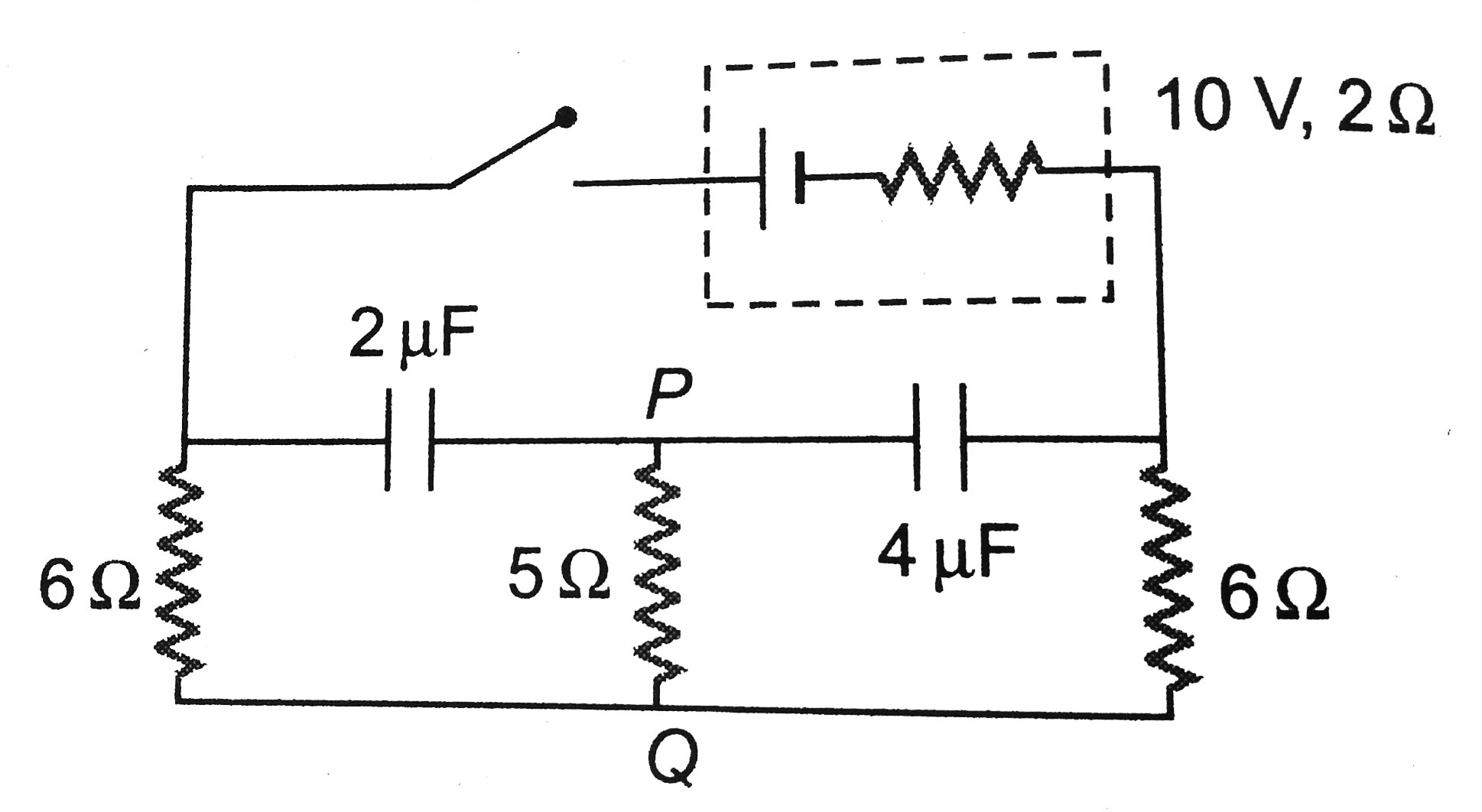A2A from P to QB2A from Q to PC6A from P to QDzeroIn the circuit in Fig. switch S1 was closed for a long time . At time t=0 the switch is opened.
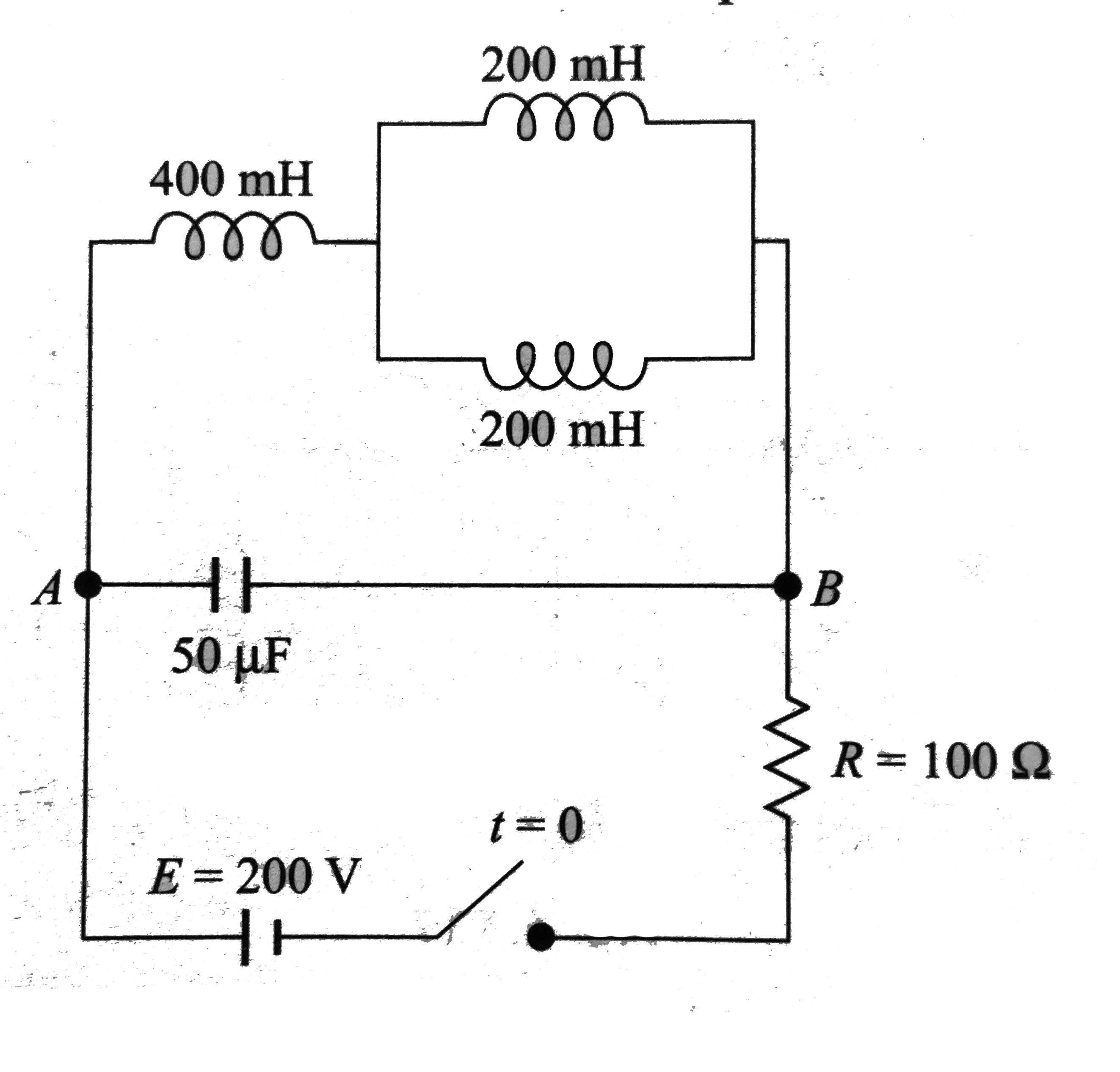
Find the angular frequency of oscillation of the charge on the capacitor.A100rads−1B200rads−1C300rads−1sD400rads−1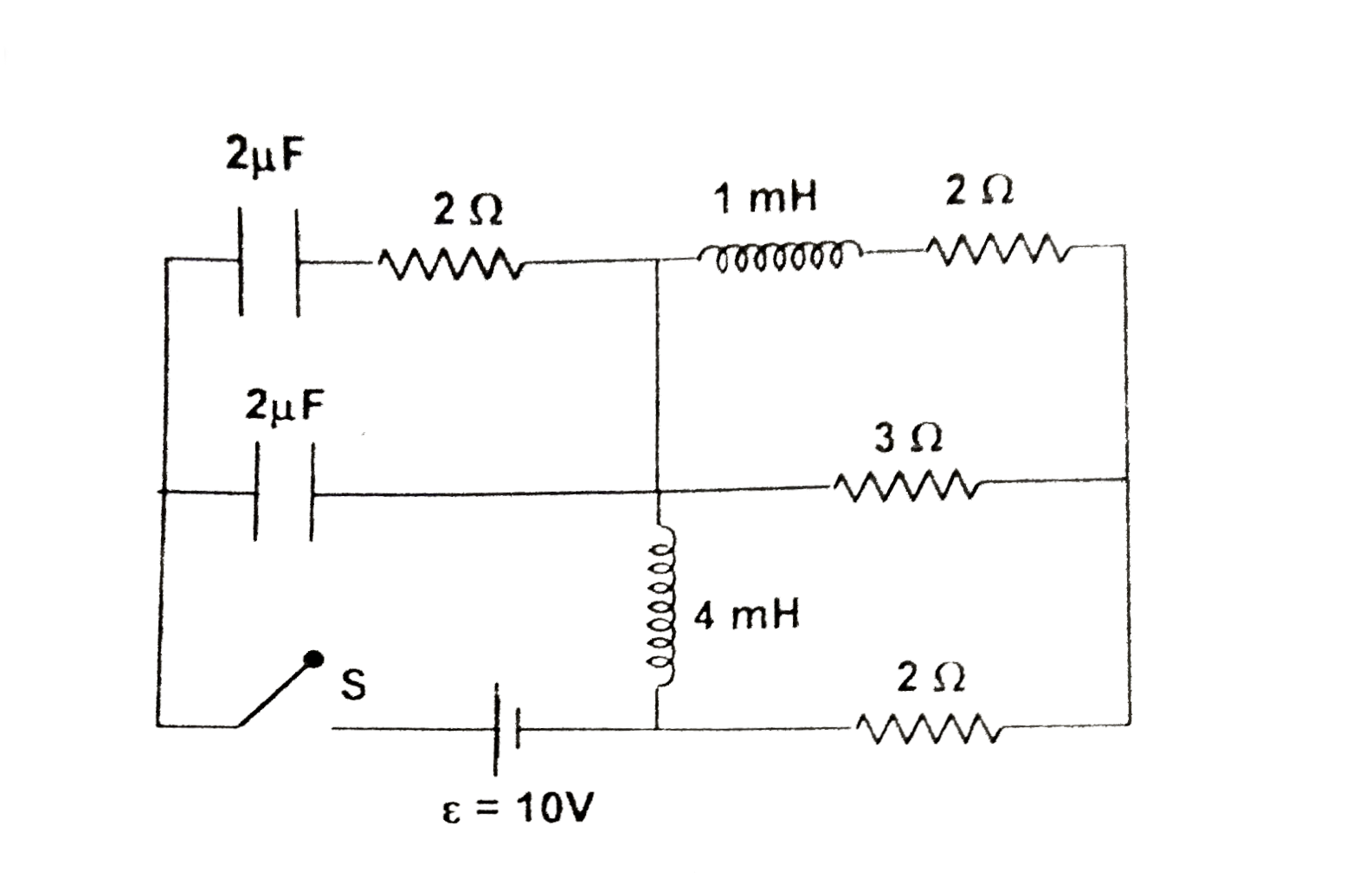
In the circuit shown, all the capacitors are initially uncharged. The current through the battery just after closing the switch 'S' isA2AB4AC5AD10A
In the circuit shown. Initially the capacitor is uncharged. The switch S is closed at time t=0. Then
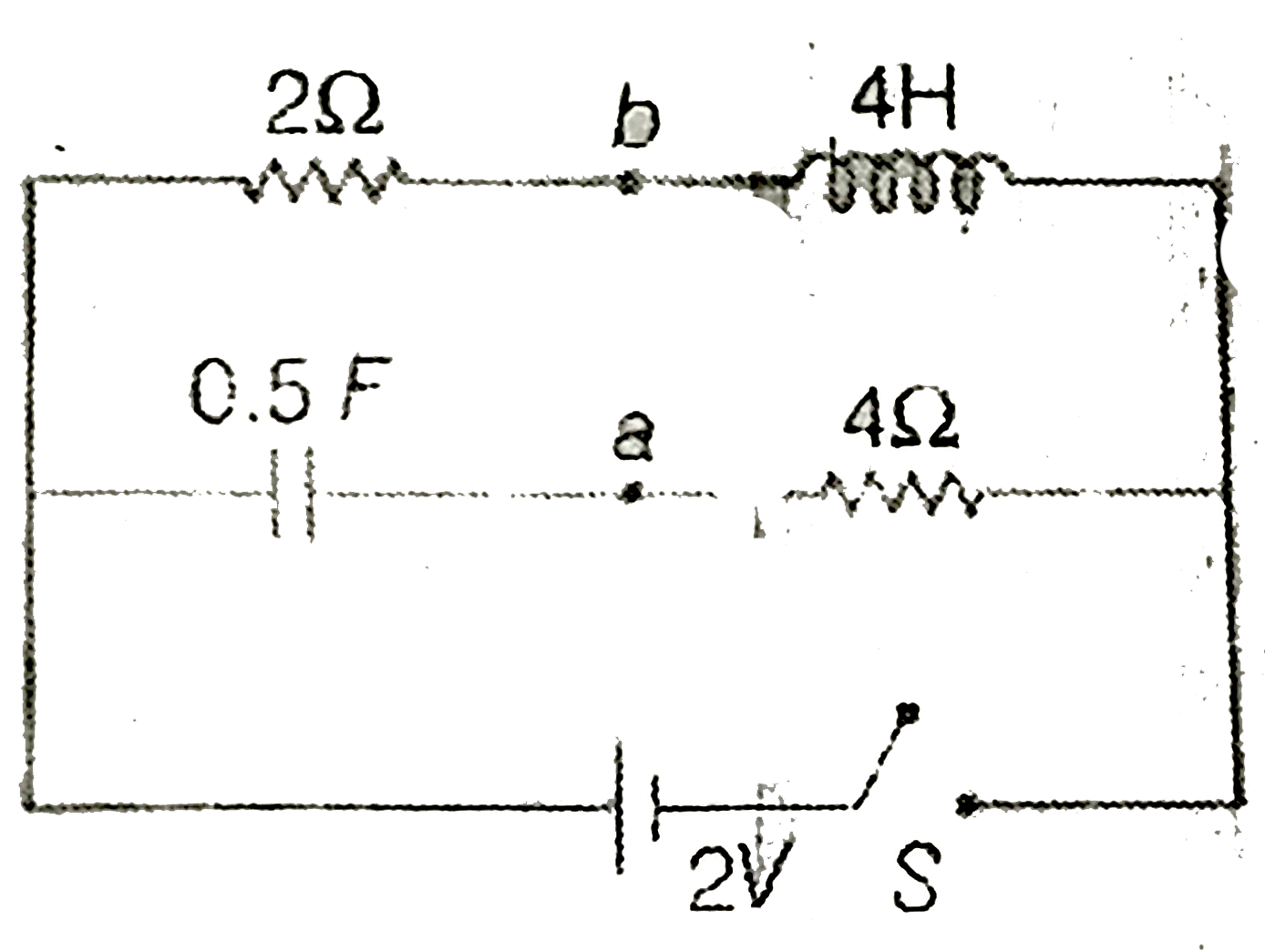
View SolutionIn the circuit shown in figure, the capacitors are initially uncharged. The current through resistor PQ just after closing the switch is
View SolutionIn the circuit in Fig. switch S1 was closed for a long time . At time t=0 the switch is opened.
Find the angular frequency of oscillation of the charge on the capacitor.
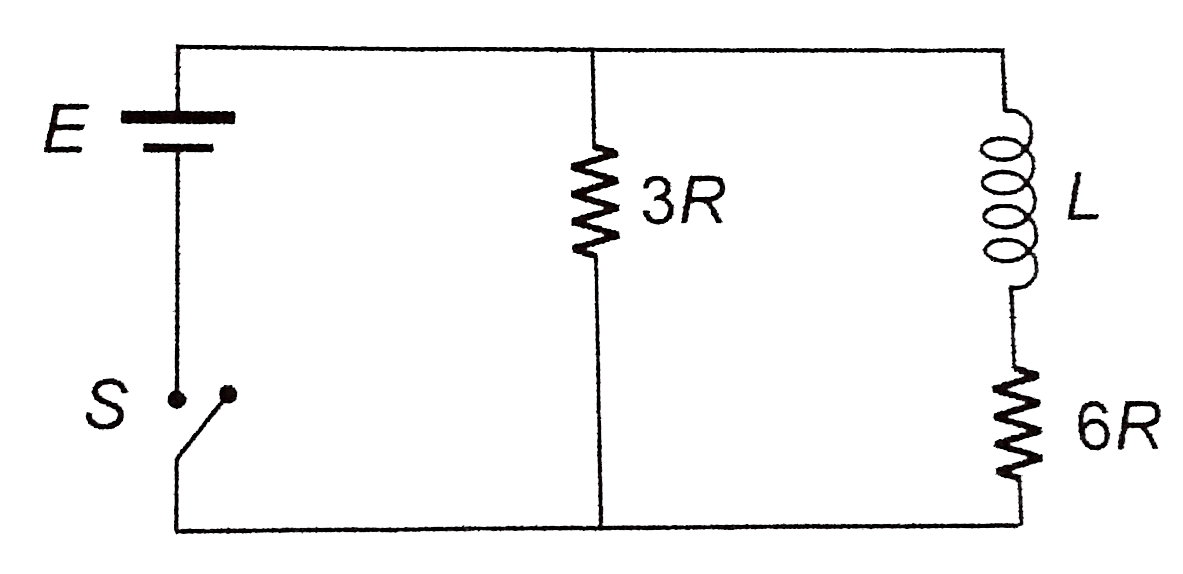
View SolutionAt t=0 , switch S is closed. Find time constant of the circuit and current through inductor as a function of time t .
View Solution-
In the circuit shown, all the capacitors are initially uncharged. The current through the battery just after closing the switch 'S' is
View Solution