Figure shows a circuit having a coil of resistance R = 2.5 Omega and i

The diagram shows a circuit having a coil of resistance $R = 10 Ω$ and inductance L connected to a conducting rod PQ which can slide on a perfectly conducting circular ring of radius 10 cm with its centre at 'P' Assume that friction & gravity are absent and a constant uniform magnetic field of 5 T exists as shown in figure. At $t = 0$ the circuit is switched on and simultaneously a time varying external torque is applied on the rod so that it rotates about P with a constant angular velocity 40 rad//s Find magnitude of this torque (in mu Nm) when current reaches half of its maximum value. Neglect the self inductance of the loop formed by the circuit.
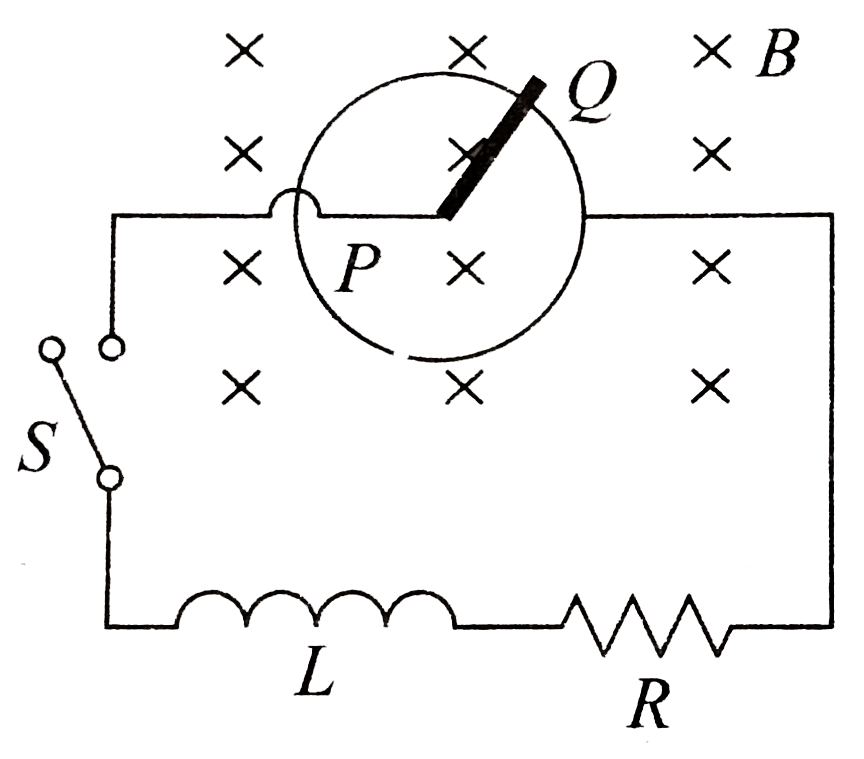
ocr_image

View Solution

The diagram shows a circuit having a coil of resistance $R = 2.5 (Ω)$ and inductance L connected to a conducting rod PQ which can slide on perfectly conducting circular ring of radius 10 cm with its centre at 'P'. Assume that friction and gravity are absent and a constant uniform magnetic field of 5 T exist as shown in Fig.
ocr_image
At t = 0, the circuit is switched on and simultaneously a time varying external torque is applied on the rod so that it rotates about P with a constant angular velocity $40 r a d / s$ . Find magnitude of this torque (in milli Nm) when current reaches half of its maximum value. Neglect the self-inductance of the loop formed by the circuit.

View Solution

The diagram shows a circuit having a coil of resistance $R = 2.5 (Ω)$ and inductance L connected to a conducting rod PQ which can slide on perfectly conducting circular ring of radius 10 cm with its centre at 'P'. Assume that friction and gravity are absent and a constant uniform magnetic field of 5 T exist as shown in Fig.
ocr_image
At t = 0, the circuit is switched on and simultaneously a time varying external torque is applied on the rod so that it rotates about P with a constant angular velocity $40 r a d / s$ . Find magnitude of this torque (in milli Nm) when current reaches half of its maximum value. Neglect the self-inductance of the loop formed by the circuit.

View Solution

The circuit shows a resistance, $R = 0.01 Ω$ and inductance L=3mH connected to a conducting rod PQ of length l=1m which can slide on a perfectly conducting circular arc of radius l with its center at P. Assume that friction and gravity are absent and a constant uniform magnetic field b=0.1T exists as shown in the figure. At t=0, the circuit is seitched on a simultaneously an external torque is applied on the rod so that it rotates about P with a constant angular velocity $ω = 2 r a d / sec$ . Find the magnitude of this torque (inN-m) at t=(0.3In 2) second.
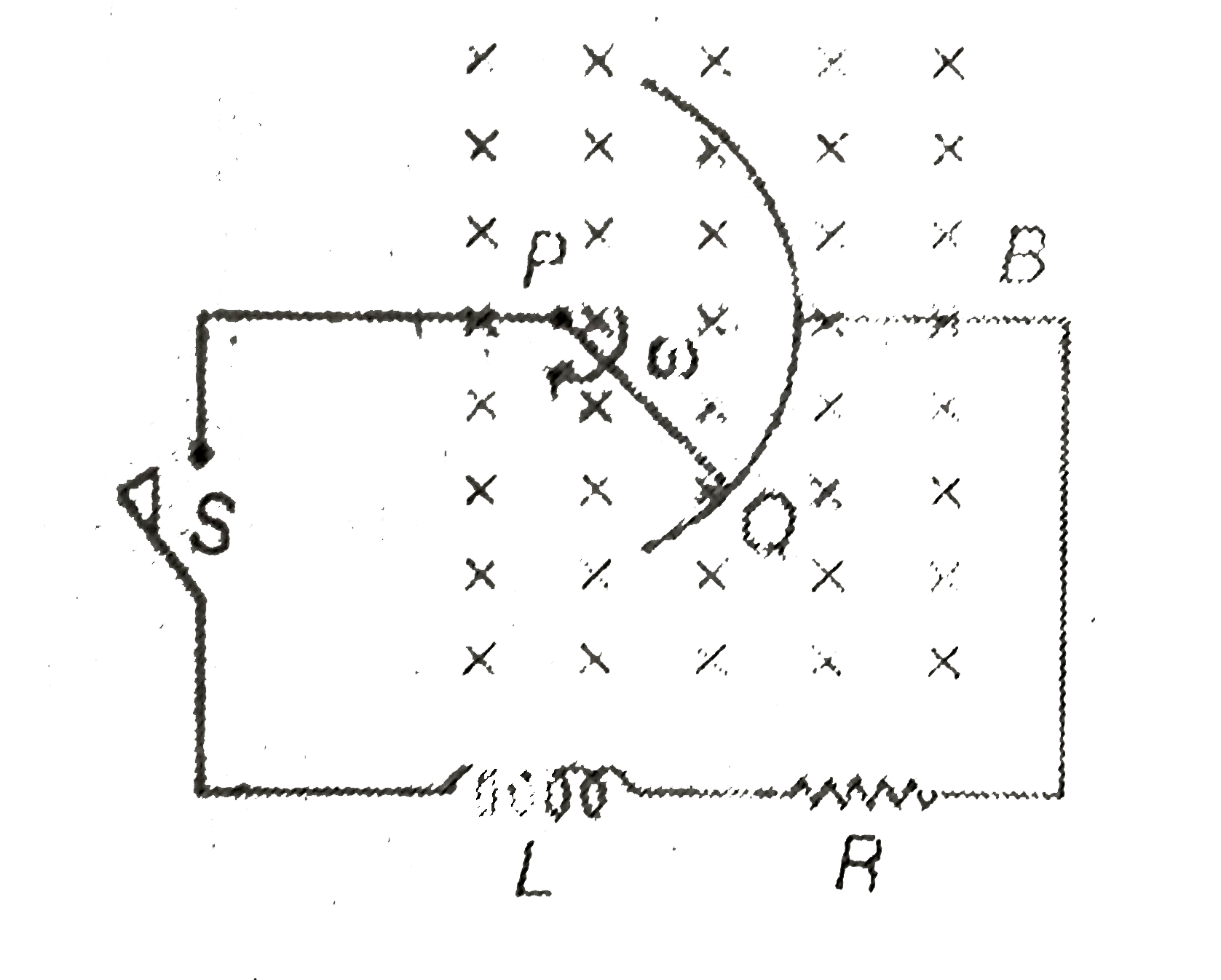
ocr_image

View Solution

The circuit shows a resistance, $R = 0.01 Ω$ and inductance L=3mH connected to a conducting rod PQ of length l=wm which can slide on a perfectly conducting circular arc of radius l with its center at P. Assume that friction and gravity are absent and a constant uniform magnetic field b=0.1T exists as shown in the figure. At t=0, the circuit is seitched on a simultaneously an external torque is applied on the rod so that it rotates about P with a constant angular velocity $ω 2 r a d / sec$ . Find the magnitude of this torque (inN-m) at t=(0.3In 2) second.
ocr_image

View Solution

The circuit shows a resistance $R = 0.01 Ω$ and inductance $L = 3 m H$ connected to a conducting rod $P Q$ of length $I = 2 m$ which can side on a perfectly conducting circular arc of radius $I$ with its centre at $P$ . Assume that friction $&$ gravity are absent and a constant uniform magnetic field $B = 0.1 T$ exists as shown in the figure. At $t = 0$ the circuit is switched on and simultaneously an external torque is applied on the rod so that it rotates about $P$ with a constant angular velocity $ω = 2$ rad/sec. Find the magnitude of this torque (in $N - m$ ) at $t = 0$ (0.3 In2) second
ocr_image

View Solution

The circuit shows a resistance, $R = 0.01 Ω$ and inductance L=3mH connected toa conducting rod PQ of length l=wm which can slide on a perfectly conducting circular arc of radius l with its center at P. Assume that friction and gravity are absent and a constant uniform magnetic field b=0.1T exists as shown in the figure. At t=0, the circuitt ois seitched on a simultaneously an external torque is applied on the rod so that it rotates about P with a constant angular velocity $ω 2 r a d / sec$ . Find the magnitude of this torque (inN-m) at t=(0.3In 2) second.
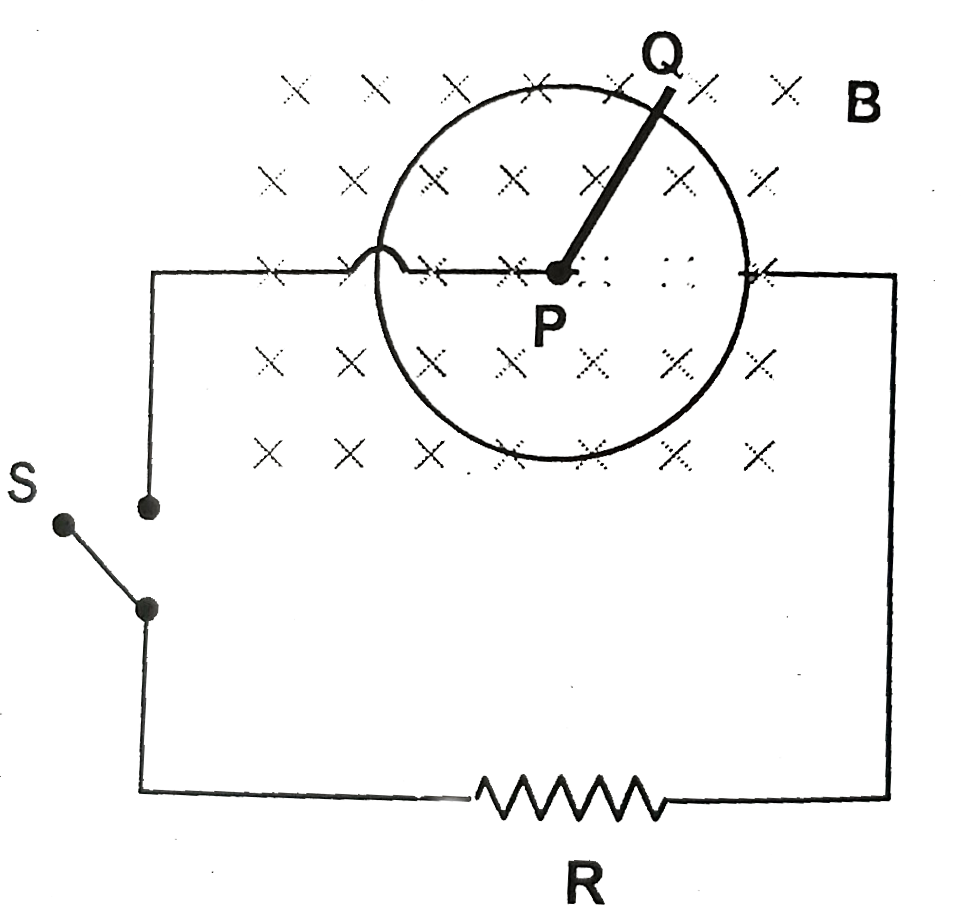
ocr_image

View Solution

A resitance $R = 1 k Ω$ connected to a conducting rod $P Q$ that can slide on a conducting circular ring of radius $2 m$ with center at $P$ . A constant uniform magnetic field 10 Tesla exist as shown in figure. At $t = 0$ , switch $' S'$ is closed and simulaneously an external torque is applied on the rod so that it rotates with constant angular velocity $20 rad / sec$ . The magnitude of power delivered by external is $20 K$ Watt. Find the value of $K$ . (Neglect the gravity, friction and self inductance of circular loop)
ocr_image

View Solution

A resitance $R = 1 k Ω$ connected to a conducting rod $P Q$ that can slide on a conducting circular ring of radius $2 m$ with center at $P$ . A constant uniform magnetic field 10 Tesla exist as shown in figure. At $t = 0$ , switch $' S'$ is closed and simulaneously an external torque is applied on the rod so that it rotates with constant angular velocity $20 rad / sec$ . The magnitude of power delivered by external is $20 K$ Watt. Find the value of $K$ . (Neglect the gravity, friction and self inductance of circular loop)
ocr_image

View Solution

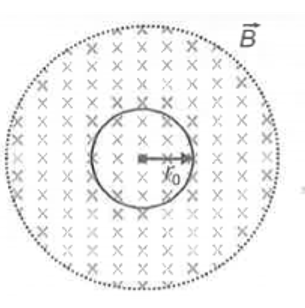
A circular conducting coil of radius $r_{0}$ , having resistance R is placed in a time varying transverse uniform magnetic field $B = 4 t^{2}$ as shown in the figure. The current in the coil at time t = 2 s is (consider all quantities are in Si units) ocr_image

View Solution

The correct Answer is: $(5)$

Induced $E M F = \frac{1}{2} B ω l^{2}$
Maximum current: $i_{0} = \frac{B ω l^{2}}{2 R}$
Torque about the hinge $P$ is
$τ = l \int 0 i (d x) B x \Rightarrow τ = \frac{1}{2} i B l^{2}$
Putting $i = i_{0} / 2$ , we get: $τ = \frac{B^{2} Ω l^{4}}{8 R} = 5 m N m$

Topper's Solved these Questions

Similar Questions

CENGAGE PHYSICS-INDUCTANCE-Exercises (integer)

The correct Answer is:(5)

Induced EMF=12Bωl2 Maximum current: i0=Bωl22R Torque about the hinge P is τ=l∫0i(dx)Bx⇒τ=12iBl2 Putting i=i0/2, we get: τ=B2Ωl48R=5mNm

Topper's Solved these Questions

Similar Questions

CENGAGE PHYSICS-INDUCTANCE-Exercises (integer)

The correct Answer is: $(5)$

Induced $E M F = \frac{1}{2} B ω l^{2}$
Maximum current: $i_{0} = \frac{B ω l^{2}}{2 R}$
Torque about the hinge $P$ is
$τ = l \int 0 i (d x) B x \Rightarrow τ = \frac{1}{2} i B l^{2}$
Putting $i = i_{0} / 2$ , we get: $τ = \frac{B^{2} Ω l^{4}}{8 R} = 5 m N m$