A 200Ω resistor is connected in series with a 5(μ)F capacitor. The voltage across the resistor is VR=(1.20V)cos(2500rads−1)t.
(a) Derive an expression for the circuit current.
(b) Determine the capactive reactance of the capacitor.
(c ) derive an experssion for the voltage across the capacitor.
This is a series curcuit. The current is the same thrugh the capacitor as through the resistor. Our target variables are current I, capactive reactance XC and capacitor voltage VC.

(a) using VR−iR, we find that current i in the resistor and through the circuit as a whole is
i−VRR=(1.20V)cos(2500rads−1)t200Ω
=(6.0×10−3A)cos(2500rads−1)t
(b) The capacitive reactance at ω=2500rads−1 is
(XC)=1ωC=1(2500rads−1_(5.0×10−6F))=80Ω
(c ) The amplitude VC of hte voltage across the capacitor is
VC0=I0XC=(6.0×10−3A)(80Ω)=0.48V
The instantaneous capcitor voltage VC is given by
VC=VC0cos(ωt−90∘)
=(0.48V)cos[(25∞rads−1)t−(π)/(2)rad].
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - ALTERNATING CURRENTEXERCISE - Solved Examples6videos
ALTERNATING CURRENT
- BOOK - CENGAGE PHYSICSCHAPTER - ALTERNATING CURRENTEXERCISE - Exercise 5.115videos
ALTERNATING CURRENT
- BOOK - CENGAGE PHYSICSCHAPTER - OSCILLATIONSEXERCISE - QUESTION BANK39videos
OSCILLATIONS
- BOOK - CENGAGE PHYSICSCHAPTER - ATOMIC PHYSICSEXERCISE - ddp.4.315videos
ATOMIC PHYSICS
Similar Questions
A 100Ω resistasnce is connected in series with a 4H inductor. The voltage across the resistor is VR=(2.0V)sin(103rad/s)t:
(a) Find the expessinocircuit current
(b) Find the inductive reactance
(c) derive an expression for the voltage across the inductor,View SolutionA 120 V, 60 Hz power source is connected across an 800Ω non inductive resistance and an unkown capacitance in series. The voltage drop across the resistor is 102 V.
(a) What is the voltahe drop acorss the capacitor ?
(b) What is the reactance of the capacitor ?View Solution
Knowledge Check
- Question 1 - Select One
A 100Ω resistance is connected in series with a 4H inductor. The voltage across the resistor is, VR=(2.0V)sin(103t).
Find the inductive reactanceA2×103 ohmB3×103 ohmC4×103 ohmD5×103 ohm - Question 2 - Select One
A 100Ω resistance is connected in series with a 4H inductor. The voltage across the resistor is, VR=(2.0V)sin(103t).
Find the expression of circuit currentA(2×10−2A)sin(103t)B(2×10−3A)sin(102t)C(2×10−3A)sin(103t)D(2×10−2A)sin(102t) - Question 3 - Select One
A 100Ω resistance is connected in series with a 4H inductor. The voltage across the resistor is, VR=(2.0V)sin(103t).
Find amplitude of the voltage across the inductor.A40VB60VC80VD90V
A resistor and a capacitor are connected in series with an a.c. source. If the potential drop across the capacitor is 5 V and that across resistor is 12 V, applied voltage is
View SolutionAn ac source of 50 V (r.m.s value) is connected across a series R - C circuit. If the r.m.s voltage across the resistor is 40 V, then the r.m.s voltage across the capacitor is
View SolutionA 100Ω resistance is connected in series with a 4H inductor. The voltage across the resistor is VR=2sin(1000t)V. The voltage across the inductors is
View SolutionA diode is connected to 220V(rms) ac in series with a capacitor as shown in fig. The voltage across the capacitor is
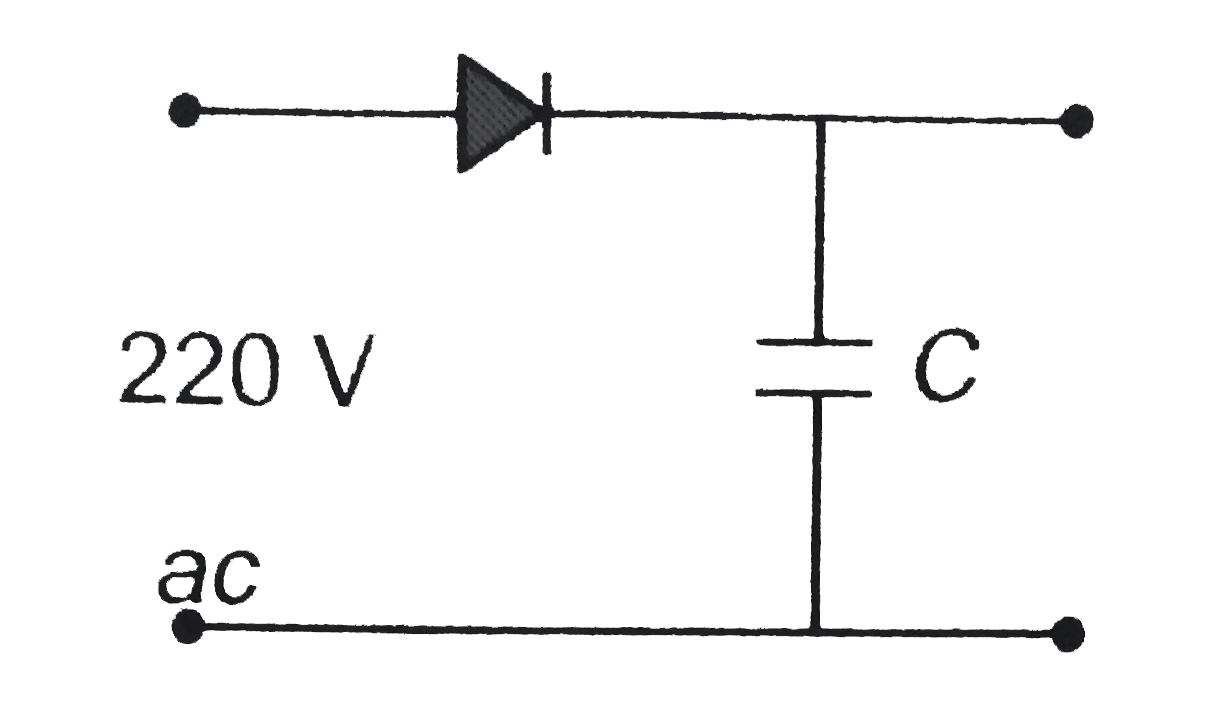 View Solution
View SolutionA resistance of 200Ω and capacitor of 15μF are connected in series to a 220 V, 50 Hz AC source. The voltage (rms) across the resistor and capacitor is that
View Solution

