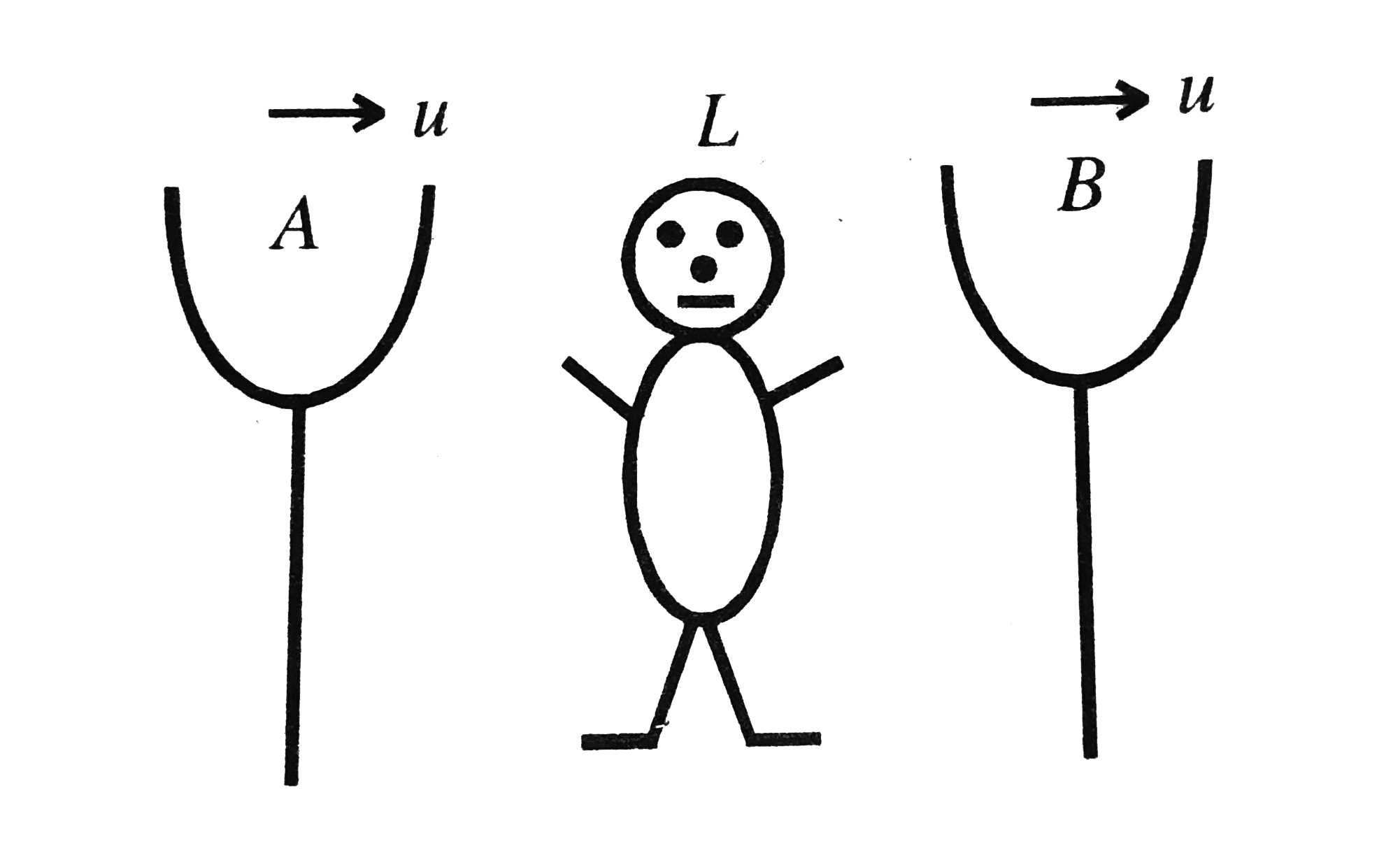Two tuning forks A and B are vibrating at the same frequency 256 Hz. A listener is standing midway between the forks. If both tuning forks move to the right with a velocity of , find the number of beats heard per second by the listerner (speed of sound in air is ).
Tuning fork A is approaching the listener. Therefore apparent frequency of sound heard by listener is
Tuning fork B is recending away from the listener. There fore apparent frequency of sound of B heard by listener is
Therefore the number of beats heard by listener per second is
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Single Correct252videos
SOUND WAVES AND DOPPLER EFFECT
- BOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Multiple Correct44videos
SOUND WAVES AND DOPPLER EFFECT
- BOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Exercise 6.272videos
SOUND WAVES AND DOPPLER EFFECT
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Comprehension Type5videos
SUPERPOSITION AND STANDING WAVES
Similar Questions
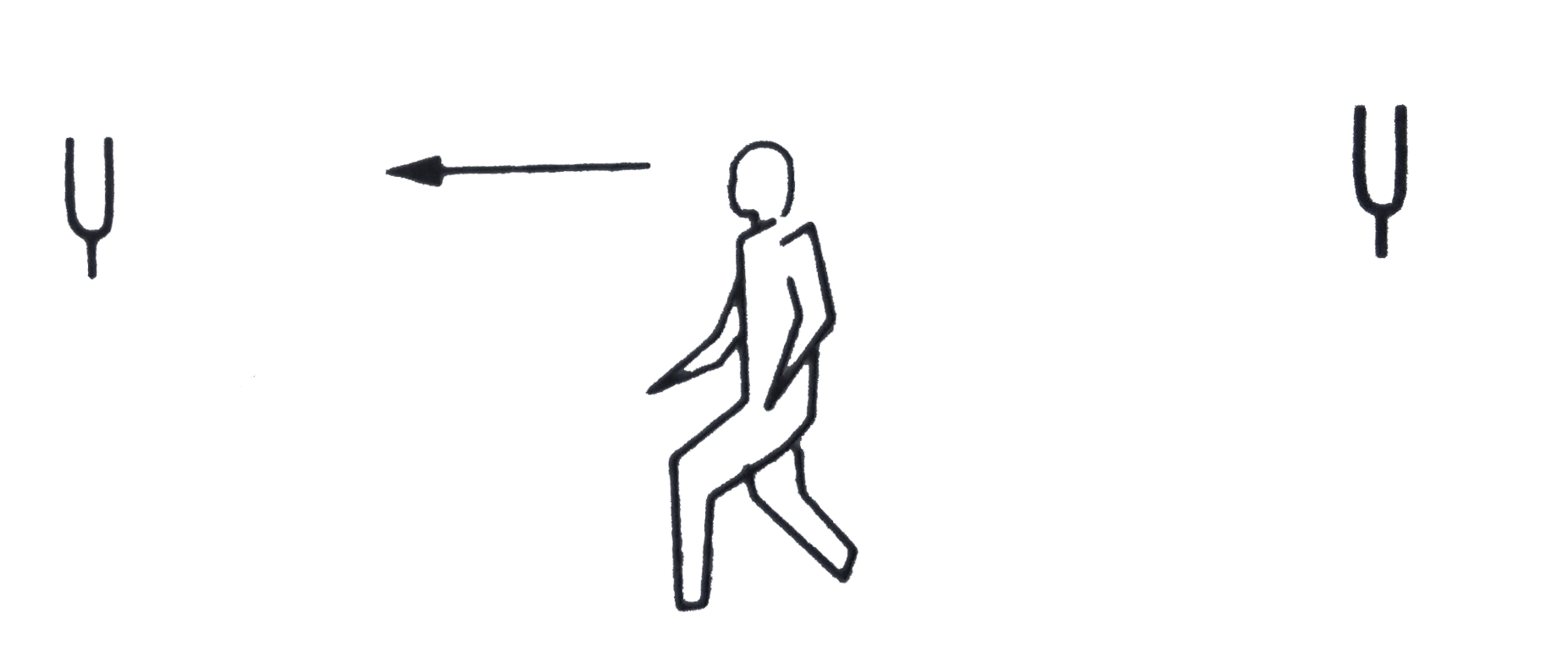
Figure shows a person standing somewhere in between two identical tunning forks, each vibrating at 512Hz.If⊥hthetun∈gforksmove→wardsrightataspeedof5.5 ms^-1,f∈dtheνmberofbeatsheardbytheliste≠r.Speedofsound∈air=330 ms^-1.
View SolutionTwo identical tuning forks vibrating at the same frequency 256 Hz are kept fixed at some distance apart. A listener runs between the forks at a speed of 3.0ms−1 so that he approaches one tuning-fork and recedes from the other. find the beat frequency bserved by the listener. Speed of sound in air =332ms−1.
.View Solution
Knowledge Check
- Question 1 - Select One
If a vibrating tuning fork of frequency 255Hz is approaching with a velocity 4m/s perpendicular to a wall. The number of beats produced per sec is (speed of sound in air =340m/s)
A3B4C5D6 - Question 2 - Select One
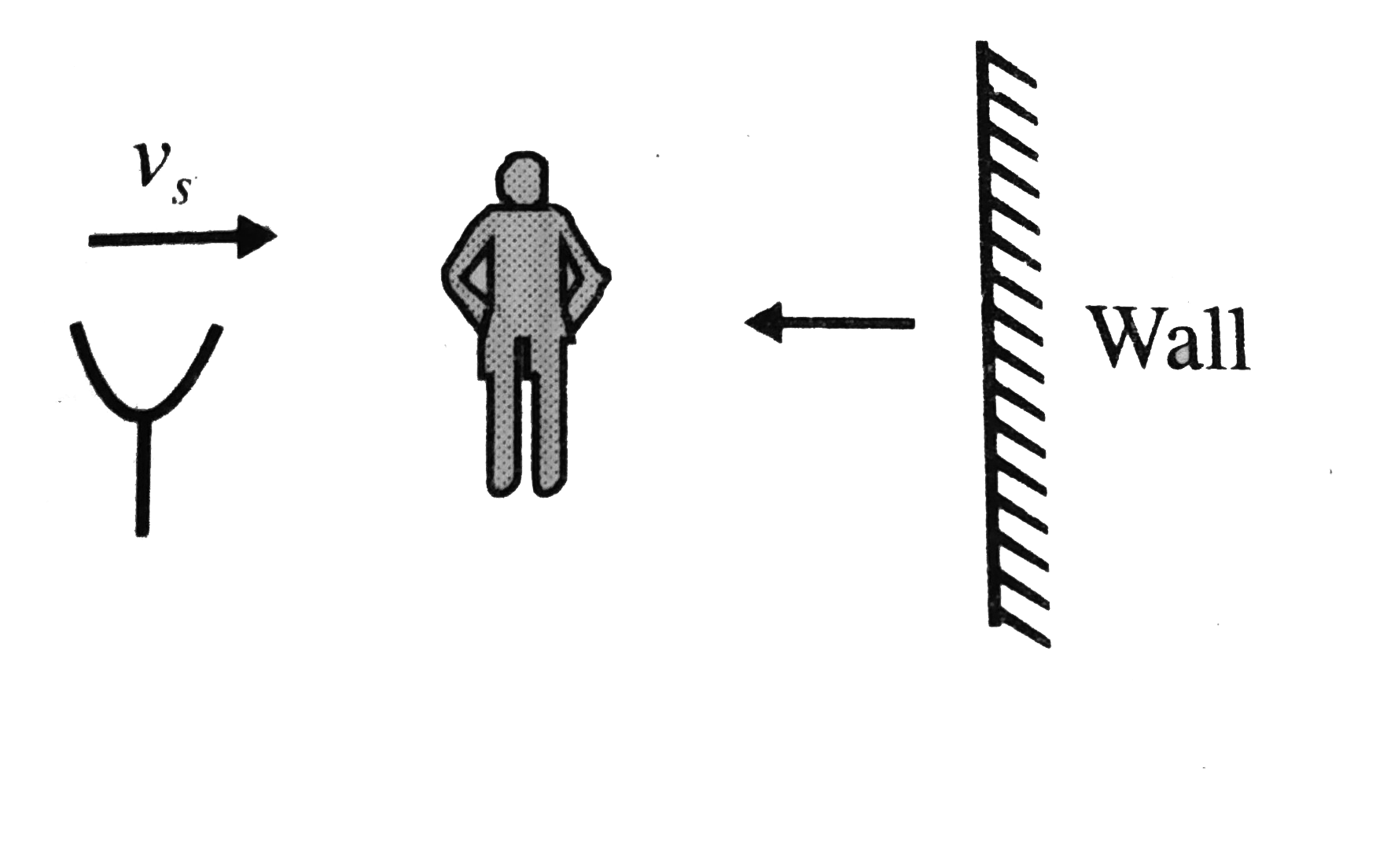
A tuning fork of frequency 380 Hz is moving towards a wall with a velocity of 4ms Then the number of beats heard by a stationary listener between direct and reflected sound will be (velocity of sound in air is 340ms)A0B5C7D10 - Question 3 - Select One
A tuning fork sounded together with a tuning fork of frequency 256 emits two beats. On loading the tuning fork of frequency 256, the number of beats heard are 1 per second. The frequency of tuning fork is
A257B258C256D254
Two tuning forks are vibrating with natural frequency of 510 Hz . One tuning fork moves away from the stationary observer, while the other moves towards him at the same speed. The observer hears beats of frequency 6 Hz. The speed of each tuning fork is -- m/s. (speed of sound in air = 340m/s)
View SolutionTwo tuning forks vibrate with the same amplitude but the frequency of the first is double the frequency of the second. Which fork produces more intense sound in air ?
View SolutionA tuning fork of frequency 328Hz is moved towards a wall at a speed of 2ms−1. An observer standing on the same side as the fork hears two sounds, one directly from the fork and the other reflected from the wall. Number of beats per second is (Velocity of sound in air 330ms−1).
View SolutionA tuning fork of frequency 256hZ is moving towards a well with a velocity of 5m/s . If the speed of sound is 330m/s , then the number of beats heard per second by a stationary observer lying between tuning fork and the well is
View SolutionWhen a tuning fork of frequency 341 is sounded with another tuning fork, six beats per second are heard. When the second tuning fork is loaded with wax and sounded with the first fork, the number of beats is two per second. The natural frequency of the second tuning fork is
View Solution