Two walls of thickness in the ratio 1:3 and thermal conductivities in the ratio 3:2 form a composite wall of a building. If the free surfaces of the wall be at temperatures 30∘C and 20∘C, respectively, what is the temperature of the interface?
1 st method : If the temperature diffrence across first wall be ΔT∘C, then that across that second wall will (10−ΔT)∘C (note)
In steady state, the rate of heat flow across the two walls will be the same.
So, considering an area A normal to the flow of heat,
dQdt=K1A(ΔT)l1=K2A(10−ΔT)l2
where K1=K,K2=3K and l1=3l,l2=2l
KAΔT3l=3KA(10−ΔT)2l⇒2ΔT=9(10−ΔT)
ΔT=8.18∘C
So, the temperature of the interface will be
30−ΔT=30−8.18=21.822C
2nd method : Using the equation, temperature of the interface
T=(K1T1/l1+K2T2/l2)(K1/l1+K2/l2)
We have T=(K(30)3l+3K(20)2l)/(K3l+3K2l)
=(10+30)(12+32)=21.82∘C
3rd method : R1=l1K1A=3lKA and R2=l2K2A=2l3KA
Effective thermal resistance R=R1+R2=113lKA
Now, thermal current i=ΔTR=30−2011l3KA=30KA11l
Also, thermal current through the first slab will be
i=(30−T)R1
i.e., 30KA11l=(30−T)KA3l⇒90=330−11T
⇒T=21.82∘C
Topper's Solved these Questions
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Exercise 1.1
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Exercise 1.2
22 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICSCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.6
20 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
The plane surface of two sheets of different metals are kept in contact with each other. The thickness of sheets 2.5cm and 3 cm respectively and the ratio of their thermal conductivities in the same order is 5:6. If the outer surfaces of the sheets are at constant temperatures of 100∘C and 10∘C respectively, calculate the temperature of interface.
View SolutionA wall consists of two layer, one of thickness 3 cm and other of 6 cm. the thermal conductivities of the materials of these layers are K and 3K respectively. The temperature of the outer surfaces of the two layers are −5∘C and 20∘C respectively. determine the temperature of the surface of contact of the two layers in the steady state.
View Solution
Knowledge Check
A compound slab is made of two parallel plates of copper and brass of the same thickness and having thermal conductivities in the ratio 4:1. The free face of copper is at 0∘C. The temperature of the internal is 20∘C. What is the temperature of the free face of brass?
A0∘CB20∘CC40∘CD100∘CTwo plates of same area are placed in contact. Their thickness as well as thermal conductivities are in the ratio 2:3. The outer surface of one plate is maintained at 10∘C and that of the other at 0∘C. What is the temperature at the common surface?
A0∘CB2.5∘CC5∘CD6.5∘CTwo walls of thickness d and d and thermal conductivities k and k are in contact. In the steady state, if the temperature at the outer T1 and T2 , the temperature at the common wall is
Ak1T1d2+k2T2d1k1d2+k2d1Bk1T1+k2d2d1+d2C(k1d1+k2d2T1+T2)T1T2Dk1d1T1+k2d2T2k1d1+k2d2
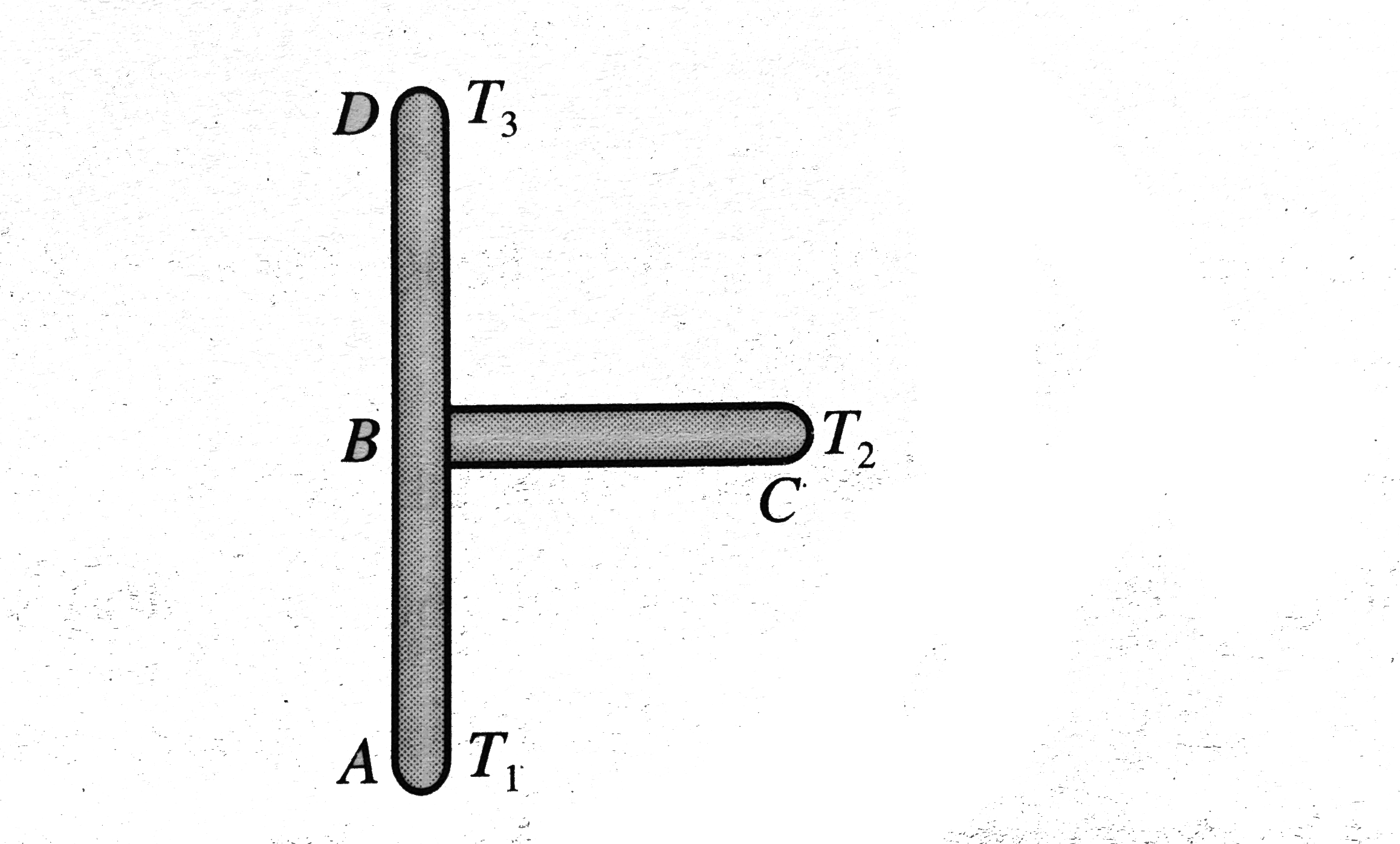
Three rods AB, BC and BD having thermal conductivities in the ratio 1:2:3 and lengths in the ratio 2:1:1 are joined as shown in Fig. The ends A, C and D are at temperature T1,T2 and T3 respectively Find the temperature of the junction B. Assume steady state.
View SolutionA composite wall of area A is made of equal thickness of lead and iron having thermal conductivities K and 2K, respectively. The temperature on the two sides of the composite wall are 100∘C and 0∘C with the layer on the hotter side. Calculate the steady -state temperature of the lead-iron interface.
View SolutionA slab consists of two parallel layers of copper and brass of the time thickness and having thermal conductivities in the ratio 1:4. If the free face of brass is at 35∘C and that of copper at 1:√2.5, the temperature of interface is
View SolutionDensities of two gases are in the ratio 1:2 and their temperatures are in the ratio 2:1, then the ratio of their respective pressure is
View SolutionA slab consists of two parallel layers of copper and brass of the same thichness and having thermal conductivities in the ratio 1:4 If the free face of brass is at 100∘C anf that of copper at 0∘C the temperature of interface is .
View Solution
