An isosceles triangles is formed with a thin rod of length l1 and coefficient of linear expansion α1, as the base and two thin rods each of length l2 and coefficient of linear expansion α2 as the two sides. The distance between the apex and the midpoint of the base remain unchanged as the temperature is varied. The ratio of lengths l1l2 is

α2α1
√α2α1
2α2α1
2√α2α1
The correct Answer is:D
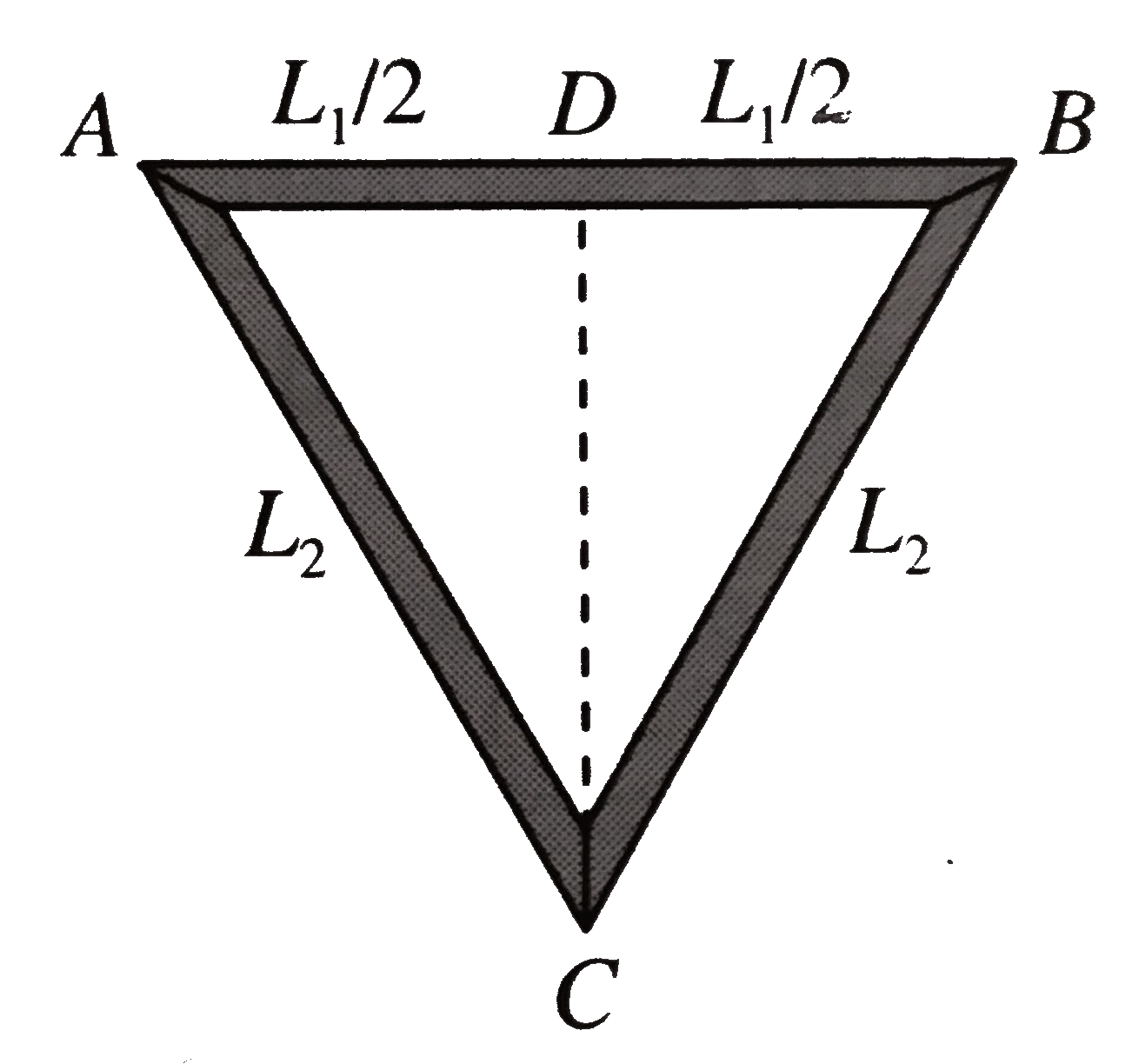
The apex of the isosceles Delta to remain at a constant distance form the knife edge. Thus, DC should remain constant before and after heating
Before expansion: In Delta ADC
(DC)2=L22−(L12)2 .(i)
After expansion:
(DC)2=[L2(1+α2t]2−[L12(1+α1t)]2 ..(ii)
Equating Eqs. (i) and (ii) we get
L22−(L12)2=[L2(1+α2t)]2−[L12(1+α1t)]2
L22−L214=L22+L22×2α2×t−L214−L214×2α1×t
(neglecting higher terms)
⇒L214(2α1t)=L22(2α2t)⇒L1L2=2√α2α1
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Multiple Correct25videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Comprehension30videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Subjective25videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.620videos
BASIC MATHEMATICS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE1videos
CENTRE OF MASS
Similar Questions
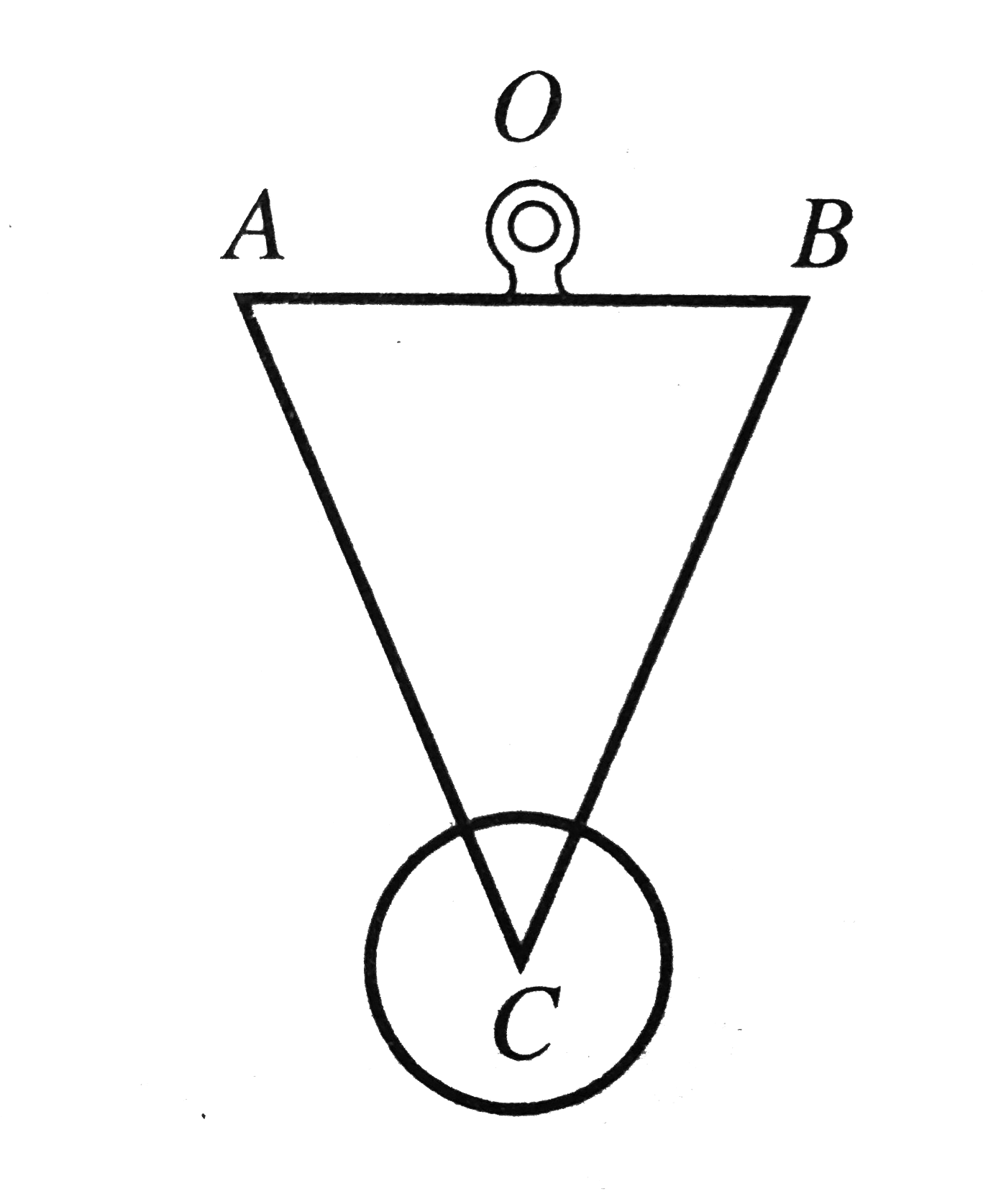
A compensated pendulum shown if Fig. is in the from of an isosceles Delta of base length l1=5cm and coefficent of linar expansion α1=18×10−6 and side length l2 and coefficient of linear expansion α2=12×10−6. find l2 so the the distance of centre of mass of the bob from suspension centre O may remain the same at all the temperature.View SolutionAmong three rods, the first two are made of same material having coefficient of linear expansion α1 and the third rod is made of material of coefficient of linear expansion α2 . The third rod forms the base of the equilateral triangle when the three rods are arranged to form an equilateral triangle. If the altitude of triangle remains constant at all temperatures, what is the ratio of α1/α2 ?
View Solution
Knowledge Check
- Question 1 - Select One
A rod of length l and coefficient of linear expansion α. Find increase in length when temperature changes from T to T+ ΔT
AlαΔTBl(1+αΔT)Cl(1+2αΔT)Dnone of these - Question 2 - Select One
A rod of length l and coefficient of linear expansion α. Find increase in length when temperature changes from T to T+ ΔT
AlαΔTBl(1+αΔT)Cl(1+2αΔT)Dnone of these - Question 3 - Select One
A cube of edge (L) and coefficient of linear expansion (α) is heated by 10C. Its surface area increases by
A6αL2B8αL2C12αL2D2αL2
There are two rods of length l1 l2 and coefficient of linear expansions are α1 and α2 respectively.
Find equivalent coefficient of thermal expansion for their combination in series.View SolutionTwo metallic rods of length l and 3l have coefficient of linear expansion α and 3α respectively. The coefficient of linear expansion ofr their series combinations, is
View SolutionA thin rod, length L0 at 0∘C and coefficient of linear expansion α has its two ends mintained at temperatures θ1 and θ2 respectively Find its new length .
View SolutionIf two rods of length L and 2L having coefficients of linear expansion α and 2α respectively are connected so that total length becomes 3L, the average coefficient of linear expansion of the composite rod equals
View SolutionTwo rods of length l1 and l2 are made of material whose coefficient of linear expansion are α1 and α2 , respectively. The difference between their lengths will be independent of temperatiure if l1/l2 is to
View Solution

