An ideal gas is initially at temperature T and volume V. Its volume is increased by ΔV due to an increase in temperature ΔT, pressure remaining constant. The quantity δ=ΔVVΔT varies with temperature as
A
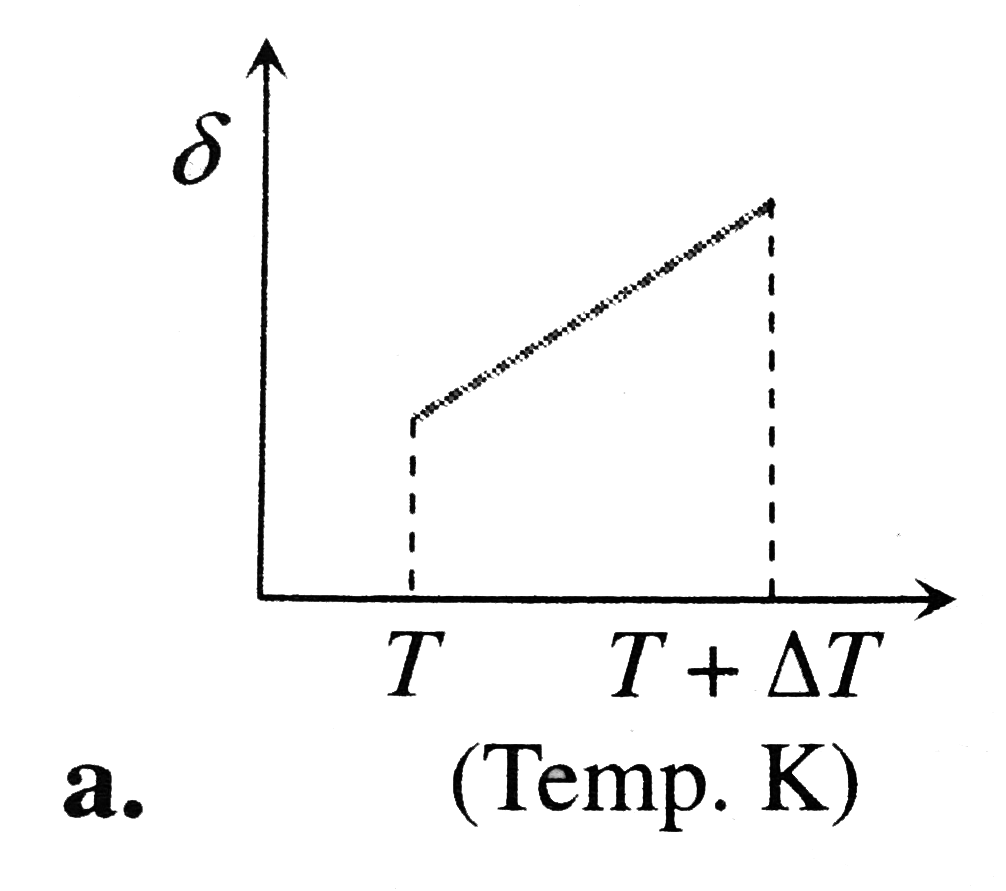
B
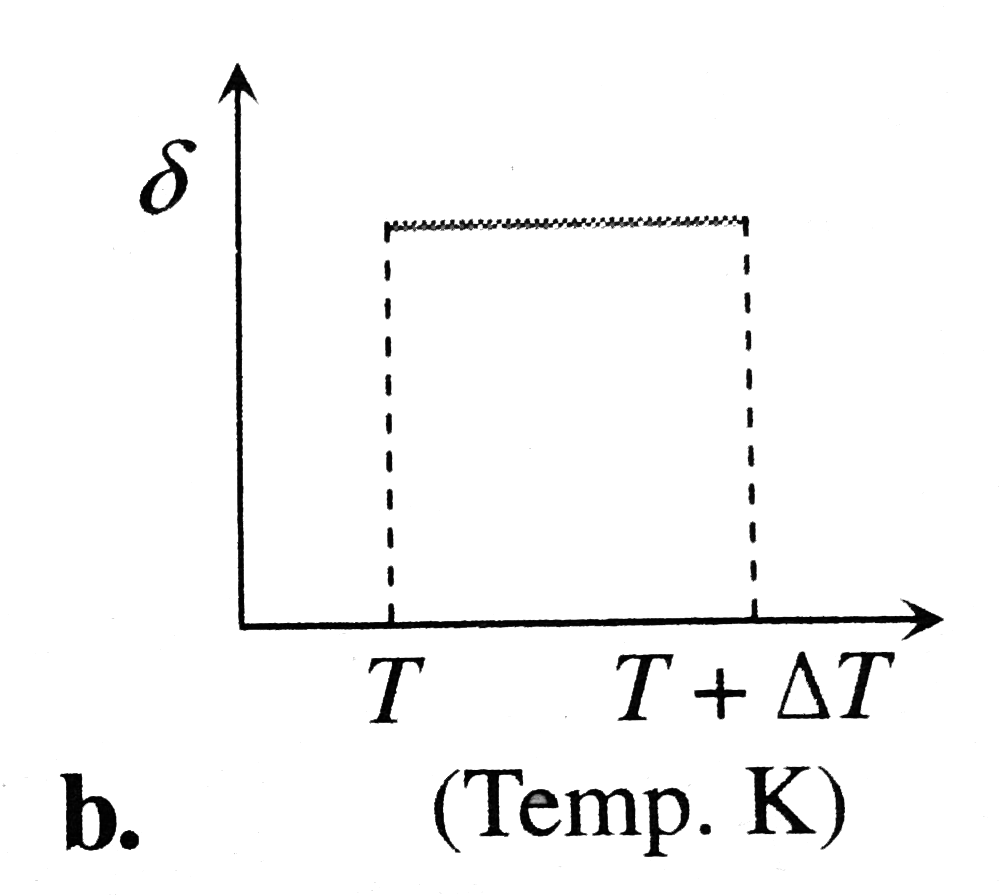
C

D

Video Solution
Text Solution
The correct Answer is:C
c. From ideal gas equation
PV=RT
PΔT=RΔT
Dividing Eq. (ii) by Eq. (i), we get
ΔTV=ΔTT⇒ΔVVΔT=1T=δ (given)
∴Δ=1T
So the graph between δ and T will be a rectangular hyperbola.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Multiple Corrects29videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Assertion-Reasoning6videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Subjective22videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression2videos
KINETIC THEORY OF GASES
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct Answer Type9videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
An ideal gas is initially at temperature T and volume V. It's volume increases by ΔV due to an increase in temperature of ΔT, pressure remaining constant. The quantity μ=ΔVVΔT varies with temperature as -
A B
B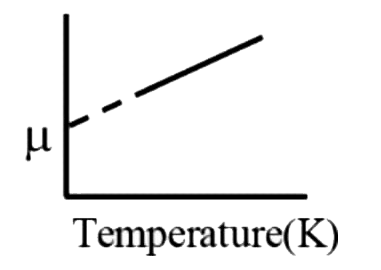 C
C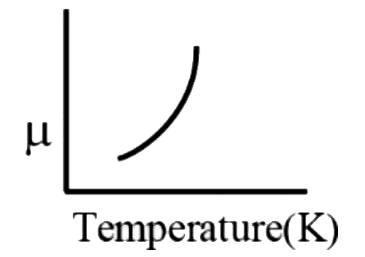 D
D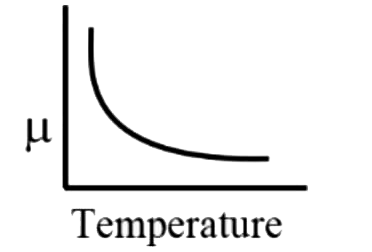
- Question 2 - Select One
An ideal gas is initially at temperature T and volume V. Its volume is increased by ΔV due to an increase in temperature ΔT, pressure remaining constant. The quantity δ=ΔVVΔT varies with temperature as
A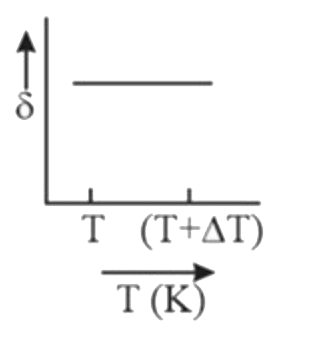 B
B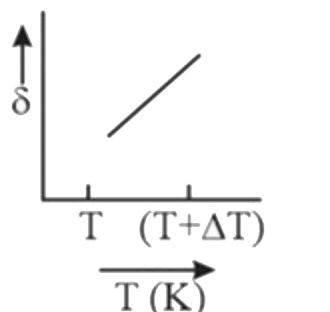 C
C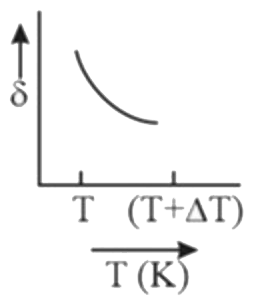 D
D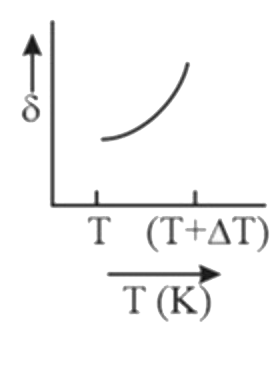
- Question 3 - Select One
A constant temperature , the volume of a gas is to be decreased by 4 % The pressure must be increased by
A0.04B0.0416C0.08D0.0386
At constant volume, temperature is increased. Then
View SolutionThe volume of a gas is increasing adiabatically. Its temperature
View SolutionBy increasing temperature of a gas by 6∘C its pressure increases by 0.4%, at constant volume. Then initial temperature of gas is
View SolutionBy increasing temperature and keeping the volume constant, the pressure of a gas will
View SolutionBy increasing temperature and keeping the volume constant, the pressure of a gas will
View Solution

