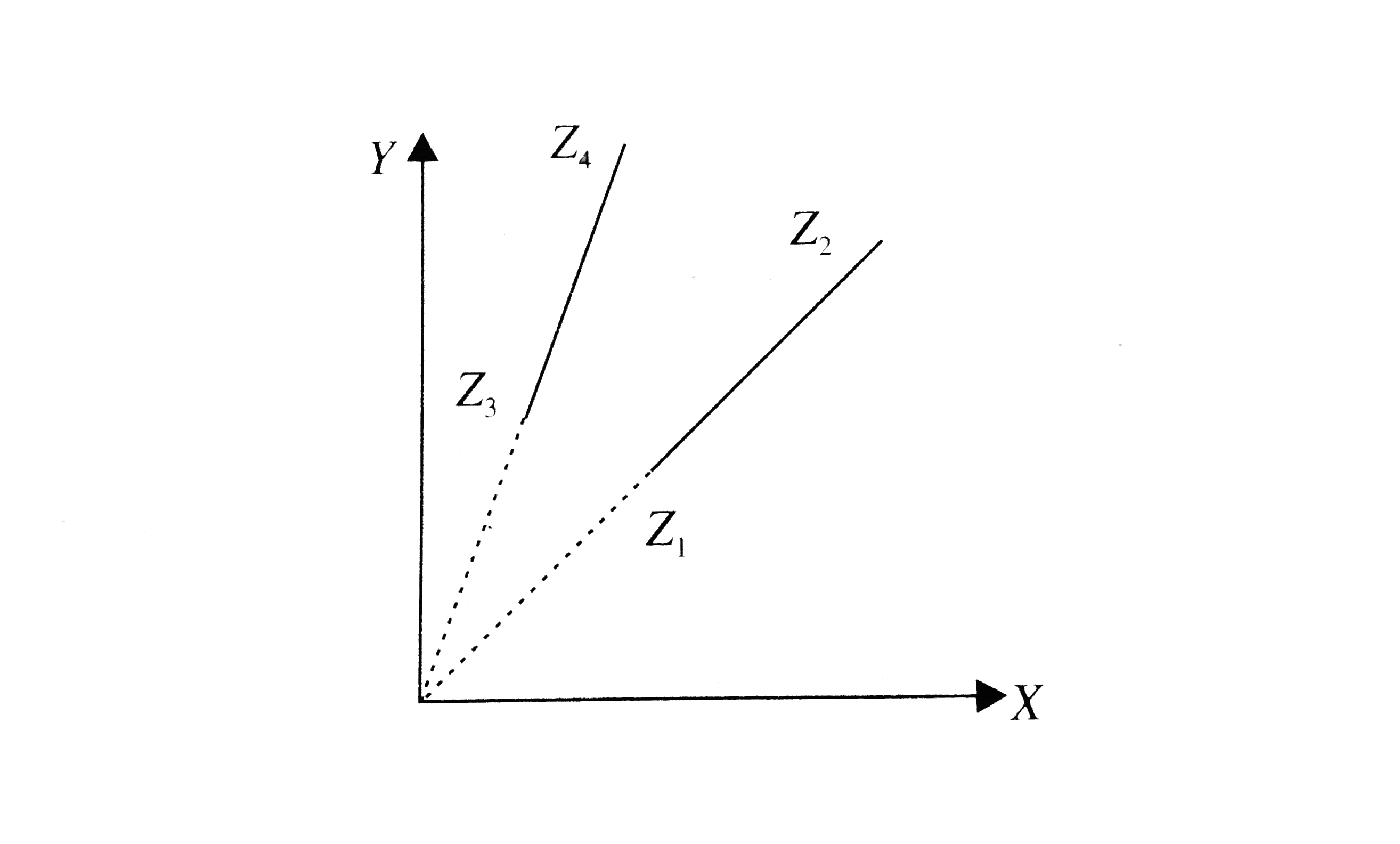
In the diagram as shown, find parameters representing x and y axes and also parameter Z, if Z1=X2,Z3=Z4 and Z2>Z3:
Volume, pressure and temperature
Temperature, volume and pressure, it is only possible option
Temperature, pressure and volume, it is only possible option.
Both (b) and (c )
The correct Answer is:D
d. If x and y axes are represented by volume and pressure respectively, and since P∝1V, then parameter temperature (Z) cannot be represented by a straight line passing through origin. Option (a) is wrong. If pressure is constant V∝T and a graph between V and T represented by a straight line passing through origin. Further VT=nRP or slope (VT)∝1P. But (slope of Z1Z2< (slope of Z3Z4). So (pressure) Z2> (Pressure Z3Z4). so (Pressure) Z2> (pressure) Z3 and Z1=Z2&Z3=Z4. So option (b) is correct For similar arguments, option (c) is also correct
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Multiple Corrects29videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Assertion-Reasoning6videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Subjective22videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression2videos
KINETIC THEORY OF GASES
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct Answer Type9videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
z1,z2,z3,z4 are distinct complex numbers representing the vertices of a quadrilateral ABCD taken in order. If z1−z4=z2−z3anda r g[(z4−z1)/(z2−z1)]=π/2 , the quadrilateral is a. rectangle b. rhombus c. square d. trapezium
ArectangleBrhombusCsquareDtrapezium - Question 2 - Select One
z1,z2,z3andz4 are the affixes of four points in the argand plane and z affix of a point such that |z−z1|=|z−z2|=|z−z3| then =|z−z4|, z1,z2,z3andz4 are
AconcyclicBtices of parallelogramCvertices of rhombusDin a straight line
if z1=3iandz2=1+2i , then find z1z2−z1
View Solutionif the complex no z1,z2andz3 represents the vertices of an equilateral triangle such that |z1|=|z2|=|z3| then relation among z1,z2andz3
View SolutionThe point z1,z2,z3,z4 in the complex plane are the vertices of a parallogram taken in order, if and only if.
(1)z1+z4=z2+z3 (2) z1+z3=z2+z4
(3) z1+z2=z3+z4 (4) z1+z3≠z2+z4View SolutionIf 2z1−3z2+z3=0, then z1,z2andz3 are represented by
View SolutionIf z1,z2,z3,z4 are the four complex numbers represented by the vertices of a quadrilateral taken in order such that z1−z4=z2−z3 and ampz4−z1z2−z1=π2 then the quadrilateral is a
View SolutionIf |z1−2|<2,|z2−4|<4,|z3−6|<6, then |z1+z2+z3| is
View Solution

