Figure shows an insulated cylinder of volume V containing monatomic gas in both the compartments. The piston is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate

The final pressures of left and right compartment respectively are
P1(P1+P2)T2P1T2+P2T1,P2(P1+P2)T1(P1T2+P2T1)
P1(P1+P2)T1P1T2+P2T2,P2(P1+P2)T1(P1T2+P2T1)
P1(P1+P2)T2P1T2−P2T1,P2(P1−P2)T1(P1T2+P2T1)
P1(P1+P2)T2P1T2+P2T1,P2(P1−P2)T1(P1T2+P2T1)
The correct Answer is:A
Applying the first law of the thermodynamics to the cylinder.
ΔQ=ΔU+ΔW
ΔQ=ΔW=0
⇒ΔU=0
n1CV(T−T1)+n2(T−T2)=0
T=(P1+P2)T1T2P1T2+P2T1
For left compartment,
P1T1=P'1T=P'1=P1(P1+P2)T2P1T2+P2T1
Similarly, P'2=P2(P1+P2)T2(P1T2+P2T1)
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Interger
Explore 11 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Assertion-Reasoning
Explore 6 Videos
- KINETIC THEORY OF GASESBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASESExercise:Compression
Explore 2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Multiple Correct Answer Type
Explore 9 Videos
Similar Questions
A diathermic piston divides adiabatic cylinder of volume V0 into two equal parts as shown in the figure. Both parts contain ideal monoatomic gases. The initial pressure and temperature of gas in left compartment are P0 and T0 while that in right compartment are 2P0 and 2T0. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium.

The heat that flown from right compartment to left compartment before thermal equilibrium is achieved is
View SolutionA diathermic piston divides adiabatic cylinder of volume V0 into two equal parts as shown in the figure. Both parts contain ideal monoatomic gases. The initial pressure and temperature of gas in left compartment are P0 and T0 while that in right compartment are 2P0 and 2T0. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium.
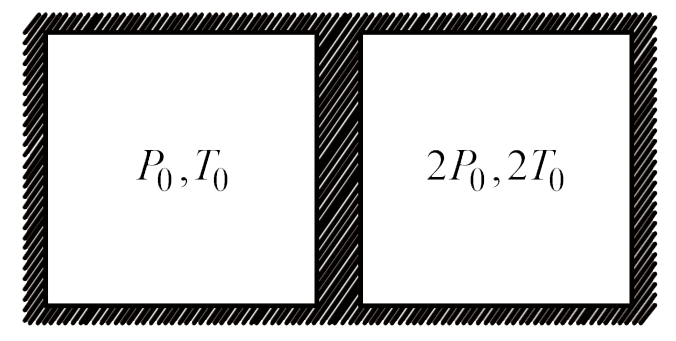
The pressure in left compartment after thermal equilibrium is achieved is
View Solution
Knowledge Check
Figure shows an insulated cylinder of volume V containing monatomic gas in both the compartments. The piston is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate

The final pressures of left and right compartment respectively areAP1(P1+P2)T2P1T2+P2T1,P2(P1+P2)T1(P1T2+P2T1)BP1(P1+P2)T1P1T2+P2T2,P2(P1+P2)T1(P1T2+P2T1)CP1(P1+P2)T2P1T2−P2T1,P2(P1−P2)T1(P1T2+P2T1)DP1(P1+P2)T2P1T2+P2T1,P2(P1−P2)T1(P1T2+P2T1)Figure shows an insulated cylinder of volume V containing monatomic gas in both the compartments. The pistone is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate

The final temperatureA(P1−P2)T1T2P1T2−P2T1B(P1+P2)T1T2P1T1−P2T2C(P1+P2)T1T2P1T2+P2T1D(P1+P2)T1T2P1T1+P2T2Figure shows an insulated cylinder of volume V containing monatomic gas in both the compartments. The piston is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate

Final volume of the left compartment.AV2(P1T2P2T1+P1T2)BV(P1T2P2T1−P1T2)CV(P1T2P2T1+P1T2)DV(2P1T2P2T1+P1T2)
A diathermic piston divides adiabatic cylinder of volume V0 into two equal parts as shown in the figure. Both parts contain ideal monoatomic gases. The initial pressure and temperature of gas in left compartment are P0 and T0 while that in right compartment are 2P0 and 2T0. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium.

If the pin which was keeping the piston fixed is removed and the piston is allowed to slide slowly such that a state of mechanical equilibrium is achieved. The volume of left compartment when piston is in equilibrium is
View SolutionFigure shows an insulated cylinder of volume V containing monatomic gas in both the compartments. The piston is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate

Final volume of right compartment.
View SolutionFigure shows an insulated cylinder of volume V containing monatomic gas in both the compartments. The pistone is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate

The heat that flows from RHS to LHS, Given T2>T1.
Now, the pin which was keeping the piston fixed is removed. and the piston is set free to move. The piston is allowed to slide slowly, such that of mechanical equilibrium is also achieved and T1P2>P1T2. Find.
View SolutionA cylinder fitted with a piston contains 0.2 moles of air at temperature 27∘ . The piston is pushed so slowly that the air within the cylinder remains in thermal equilibrium with the surroundings. Find the approximate work done by the system if the final volume is twice the initial volume
View SolutionTen moles of a diatomic perfect gas are allowed to expand at constant pressure. The initial volume and temperature are V0 and T0 respectively. If 72RT0 heat is transferred to the gas, then the final volume and temperature are
View Solution
