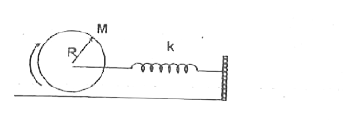
A solid cylinder of mass is attached to a horizontal spring with force constant . The cylinder can roll without slipping along the horizontal plane. (See the accompanying figure.) Show that the center of mass of the cylinder executes simple harmonic motion with a period , if displaced from mean position.

NA
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Solved Example
15 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.1
23 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A solid sphere of mass m is attached to a light spring of force constant k so that it can roll without slipping along a horizontal surface. Calculate the period of oscillation made by sphere.

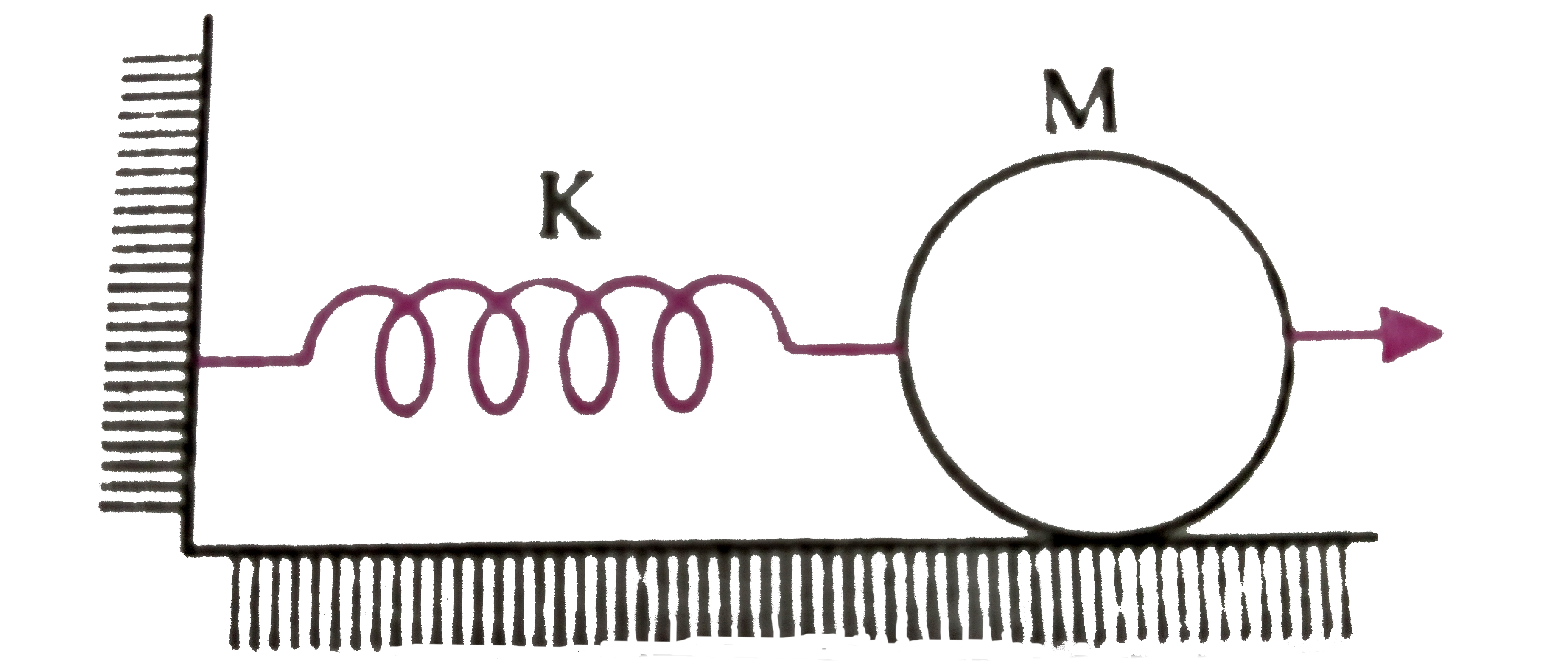
View SolutionA small solid cylinder of mass M attached to horizontal massless spring can roll without slipping along a horizontal surface. Show that if the cylinder is displaced slightly and released, it executes S.H.M. Also find its time period.
View Solution
Knowledge Check
A disc of mass M is attached to a horizontal massless spring of force constant K so that it can roll with out slipping along a horizontal surface. If the disc is pulled a little towards right and then released, its centre of mass executes SHM with a period of
 A2π√MKB2π√3MKC2π√M2KD2π√3M2K
A2π√MKB2π√3MKC2π√M2KD2π√3M2KA solid cylinder of mass M and radius R rolls without slipping down an inclined plane of length L and height h. What is the speed of its center of mass when the cylinder reaches its bottom
A√34ghB√43ghC√4ghD√2ghA solid uniform cylinder of mass M attached to a massless spring of force constant k is placed on a horizontal surface in such a way that cylinder can roll without slipping. If system is released from the stretched position of the spring, then the period will be-
_E01_059_Q01.png) A2π√MkB2π√3m2kC2π√M2kD2π√2M3k
A2π√MkB2π√3m2kC2π√M2kD2π√2M3k

A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder is
View SolutionA solid cylinder of mass M and radius R rolls without slipping on a flat horizontal surface. Its moment of inertia about the line of contact is ?
View SolutionA solid cylinder of mass M and radius R rolls without slipping down an inclined plane of length L and height h. What is the speed of its centre of mass when the cylinder reaches its bottom ?
View SolutionA solid cylinder of mass M and radius R rolls without slipping down on inclined plane of length L and height h what is the speed of its centre of mass when the cylinder reaches its bottom?
View SolutionA solid cylinder of mass M and radius R rolls without slipping down on inclined plane of length L and height h what is the speed of its centre of mass when the cylinder reaches its bottom?
View Solution
