figure (a) and (b) represent spring- block system. If m is displacement slightly , find the time period of oscillation of the system.
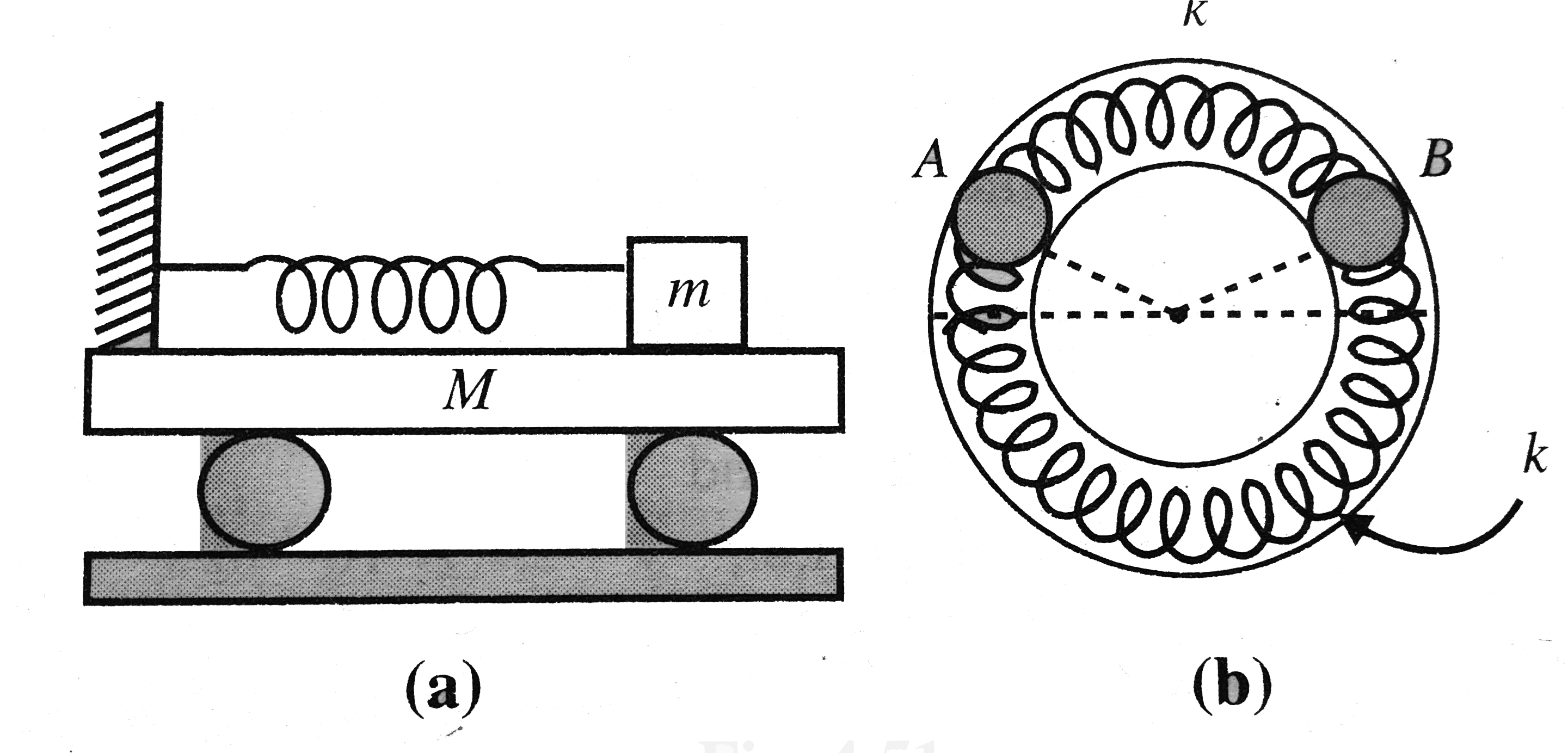
both the cases are as follows:
Reduced mass of the system Reduced mass of the system
μ=(mMm+m) μ=mMm+m=m2
T=2π√μk and ke=k+k=2k
T=2π√μke
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Solved Example
15 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.1
23 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
Knowledge Check
In a spring block system if length of the spring is increased by 4%, then time period
Aincrease by 2%Bincrease by 0.5%Cdecrease by 2%Ddecrease by 0.5%A body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is
 A2π√m3KB2π√3m2KC2π√2m3KD2π√3Km
A2π√m3KB2π√3m2KC2π√2m3KD2π√3Km
Find the period of oscillation of the system shown in figure.

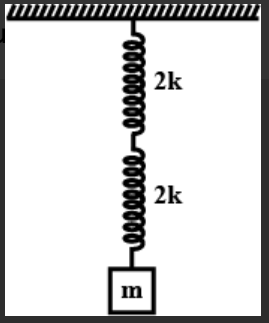
View SolutionIn the given spring block system if k=25π2Nm−1, find time period of oscillation.

View SolutionThe time period of oscillation of the block as shown in figure is
View SolutionSpring mass system is shown in figure. Find the elastic potential energy stored in each spring when block is at its mean position. Also find the time period of vertical oscillations. The system is in vertical plane.

View SolutionSpring mass system is shown in figure. Find the elastic potential energy stored in each spring when block is at its mean position. Also find the time period of vertical oscillations. The system is in vertical plane.

View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View Solution

