In the above question,if both are in opposite direction. Then the velocity of the pulse w.r.t. to groun will be:
ωL
ωL2(π)
ωLπ
0
The correct Answer is:d
VP/R=ωLπ VP/G−(−wL2π)=wL2π
∴VP/G=0
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Single Correct Answer1videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Multiple Correct25videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Subjective16videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICSCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct9videos
TRANSMISSION OF HEAT
- BOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
(A): Relative velocity of A w.r.t. B is greater than the velocity of either, when they are moving in opposite directions.
(R): The relative velocity between any two bodies is equal to the sum of the velocities of the two bodies.View SolutionAssertion: Relative velocity of A w.r.t B is greater than the velocity of either, when they are moving in opposite directions.
Reason: Relative velocity of A w.r.t B=→vA−→vBView Solution
Knowledge Check
- Question 1 - Select One
In the above question, if the motion of the pulse and rotation of the loop, both are in same direction then the velocity of the pulse w.r.t. to ground will be:
AωLBωL2(π)CωLπDωL4π2 - Question 2 - Select One
In the above question, the order w.r.t. B is:
A3B2C1Dzero - Question 3 - Select One
The velocity of image w.r.t ground in the below figure is
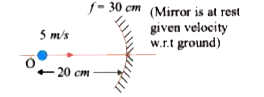 A45 m/s and approaches the mirrorB45 m/s and moves away from the mirrorC60 m/s and approaches the mirrorD60 m/s and moves away from the mirror
A45 m/s and approaches the mirrorB45 m/s and moves away from the mirrorC60 m/s and approaches the mirrorD60 m/s and moves away from the mirror
Two cars are moving is one a same line dimension in opposite direction with the same speed v. The relative velocity of two cars w.r.t. each other is
View SolutionIn the above question what will be the displacement of particle in x-direction when its velocity makes 60∘ angle with initial velocity?
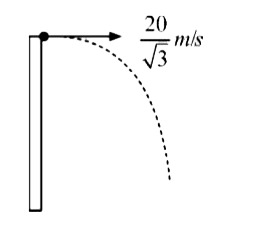 View Solution
View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:
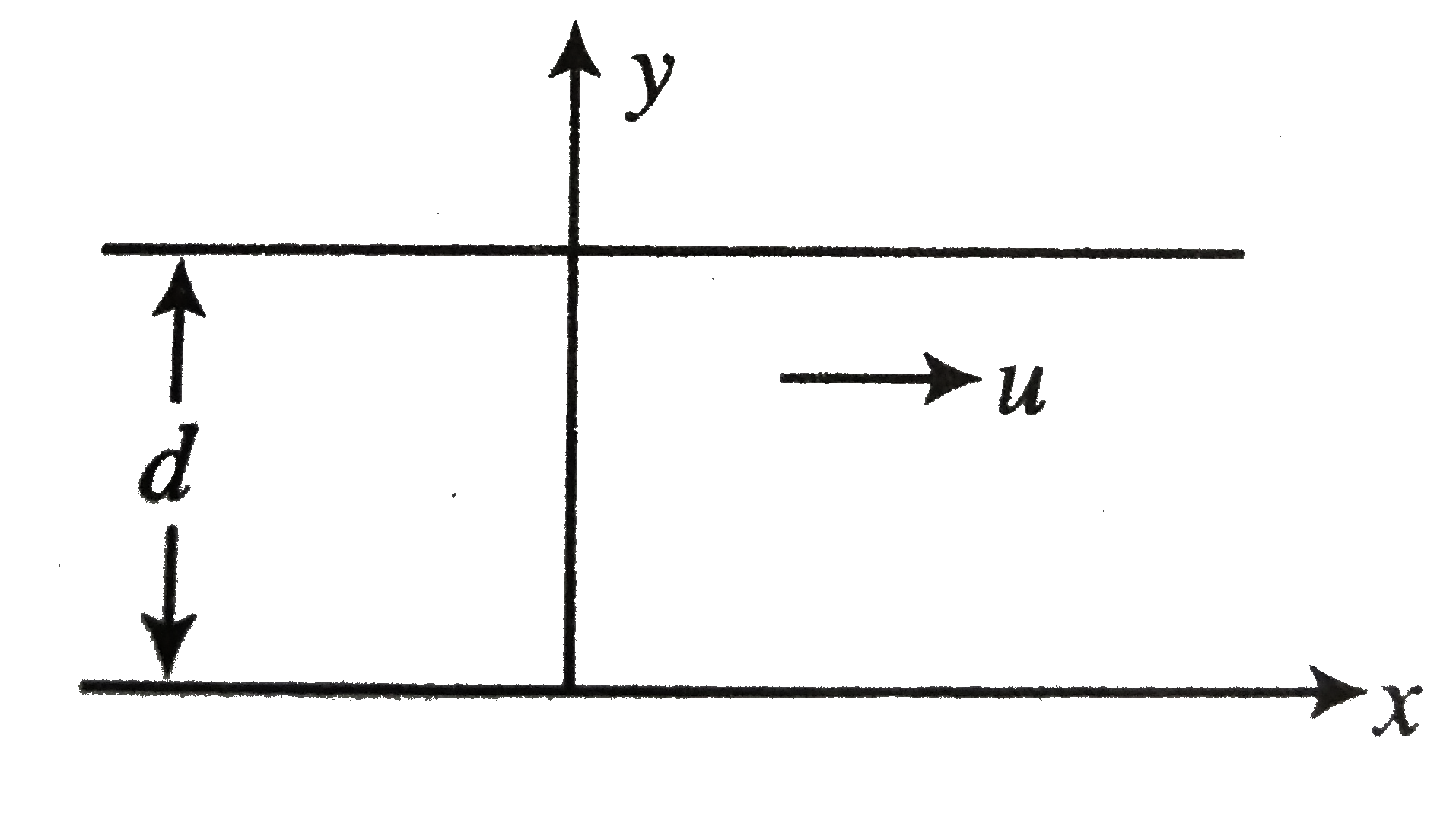
→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:

→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:

→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.View Solution

