Find the resultant amplitude and the phase difference between the resultant wave and the first wave , in the event the following waves interfere at a point , $y_{1} = (3 c m) sin ω t$ ,
$y_{2} = (4 c m) sin (ω t + \frac{π}{2}), y_{3} = (5 c m) sin (ω t + π)$

Video Solution

Text Solution

Verified by Experts

The amplitudes can be added vectorially , with angle between them as their phase difference .
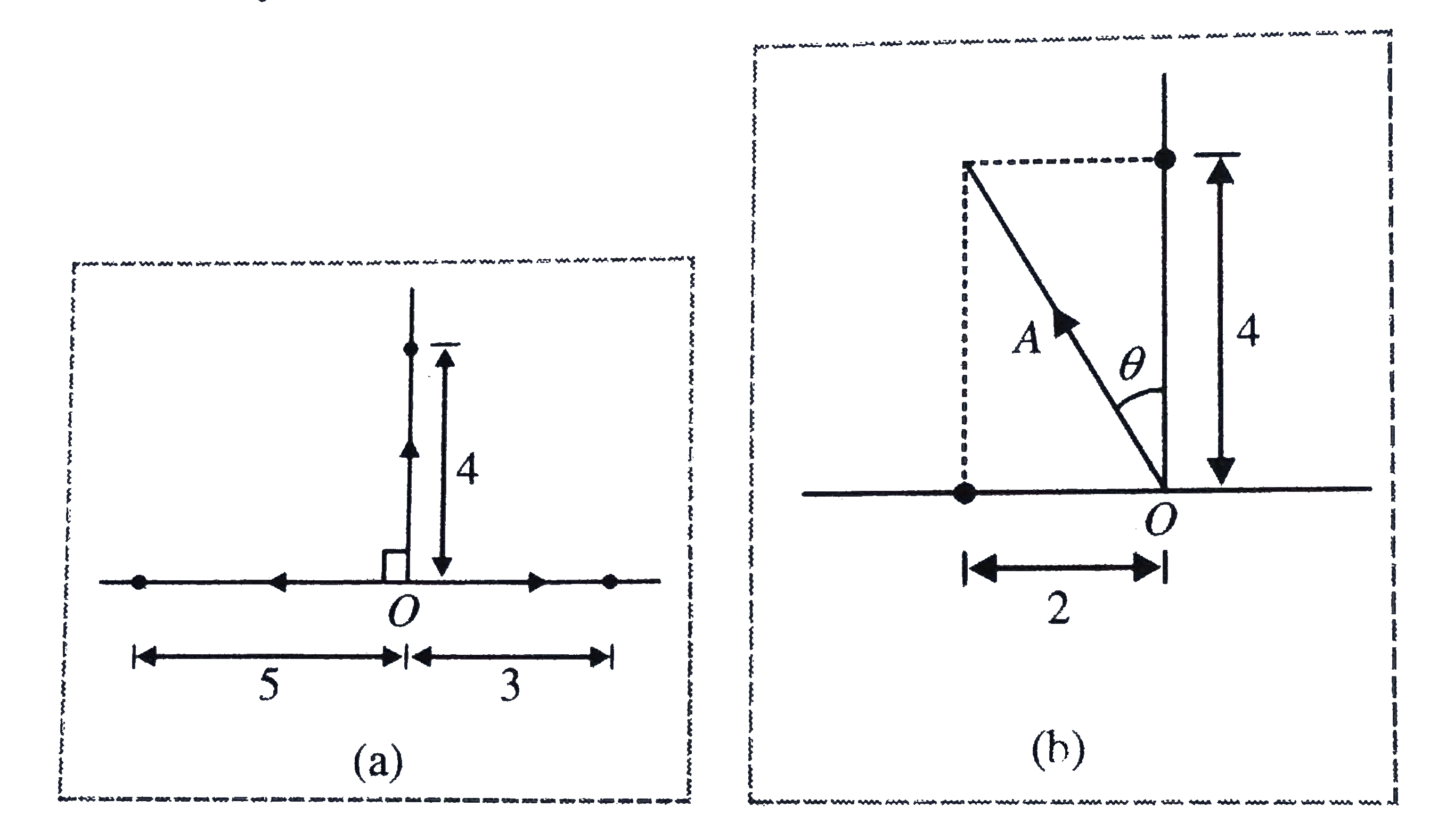
All these are shown in Fig . S 7 .1(a). The resultant amplitude $' A'$ due to the interference of three waves is evidently from Fig. S7.1(b) given by
$A = \sqrt{4^{2} + 2^{2}} = 2 \sqrt{5} c m$
Also , $tan θ = \frac{2}{4} = \frac{1}{2}$
$θ = {tan}^{- 1} (\frac{1}{2})$
Therefore , the resultant wave leads the first wave by an angle
$\frac{π}{2} + {tan}^{- 1} (\frac{1}{2})$

Updated on:21/07/2023