A sound wave starting from source S, follows two paths AOBandACB to reach the detector D. If ABC is an equilateral traingle , of side l and there is silence at point D, the maximum wavelength (λ) of sound wave must be

l
2l
3l
4l
The correct Answer is:B
Path difference =(2l−l)=λ/2 (for minimum)
λ=2l
Topper's Solved these Questions
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICSCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Multiple
26 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICSCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Assertion - Reasoning
6 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICSCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Subjective
24 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - 24
1 Video
Similar Questions
Two sound waves emerging from a source reach a point simultaneously along two paths. When the path difference is 12cm or 36cm, then there is a silence at that point. If the speed of sound in air be 330m/s, then calculate maximum possible frequency of the source.
View SolutionSound waves from a tuning fork A reach a point P by two separate paths ABP and ACP. When ACP is greater than ABP by 11.5 cm, there is silence at P. When the difference is 23 cm the sound becomes loudest at P and when 34.5 cm there is silence again and so on. Calculate the minimum frequency of the fork if the velocity of sound is taken to be 331.2m/s.
View Solution
Knowledge Check
A sound wave starting from source S, follows two paths SEFDandSEABFD. If AB=1,AE=BF=0.6l and wavelength of wave is λ=11m. If maximum sound is heard at D , then maximum value of length l is
 A11mB6mC2.5mD5m
A11mB6mC2.5mD5mIn the case of sound waves, wind a blowing from source to reciver with speed UW. Both source and receiver are stationary.If λ0 is the original wavelength with no wind and V is speed of sound in air then wavelength as received is given by :
Aλ0B(V+UWV)λ0C(V−UWV)λ0D(VV+VW)λ0In a large room , a person receives direct sound waves from a source 120m away . He also receives waves from the same source which reach him after being reflected from the 5m high ceiling at a point halfway between them . For which wavelengths will these two sound waves interfere constructively ?
A0.21 mB0.44 mC0.36 mD0.45 m
Sound waves from a tuning fork A reacha point P by two separate paths ABP and ACP. When ACP is greater than ABP by 11.5cm, there is silence at p. When the difference is 23cm the sound becomes loudest at P and 34.5cm there is silence again and so on. Calculate the minimum frequency of the fork if the velocity of sound is taken to be 331.2m/s.
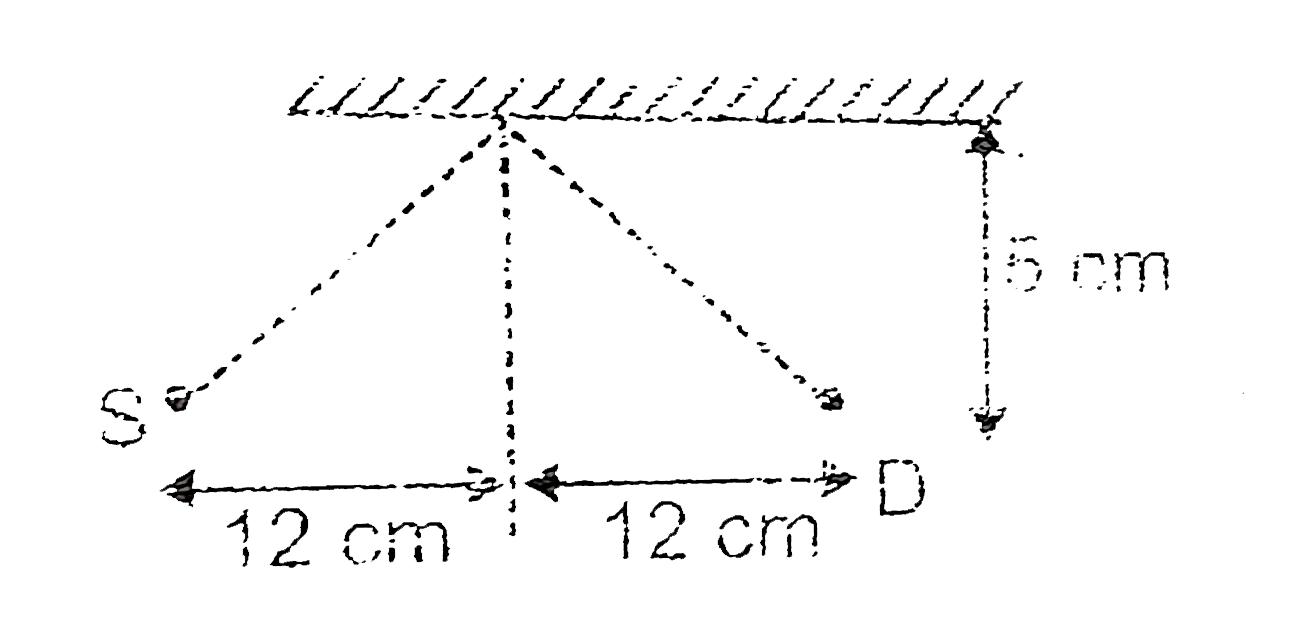
View SolutionA sound source, detector and a cardboard are arranged as shown in figure. The wave is reflected from the cardboard at the line symmetry of source edetector. Initially the path difference between the reflected wave and the direct wave is one third of the wavelength of sound. Find the minimum distance by which the cardboard should be moved upwards so that both waves are in phase.
View SolutionA narrow tube is bend in the form of a circle of radius R, as shown in the figure. Two small holes S and D are made in the tube at the positions right angle to each other. A source placed at S generated a wave of intensity I0 which is equally divided into two parts : One part travels along the longer path, while the other travels along the shorter path. Both the parts wave meet at the point D where a detector is placed.
_E01_100_Q01.png)
If the minima is formed at the detector then, the magnitude of wavelength λ of the wave produced is given by :-
View SolutionA narrow tube is bent in the form of a circle of radius R, as shown in figure. Two small holes S and D are made in the tube at the position at right angle to each other. A source placed at S generates a wave of intensity I0 which two parts: one part travels along the longer path, while the other travels along the shorter path. Both the waves meet at point D where a detector is placed.

2. If a minima is formed at the detector, then the magnitude of wavelength λ of the wave produced is given by
View SolutionA narrow tube is bend in the form of a circle of radius R, as shown in the figure. Two small holes S and D are made in the tube at the positions right angle to each other. A source placed at S generated a wave of intensity I0 which is equally divided into two parts : One part travels along the longer path, while the other travels along the shorter path. Both the parts wave meet at the point D where a detector is placed.
_E01_099_Q01.png)
If a maximum is formed at the detector then, the magnitude of wavelength λ of the wave produced is given by :-
View Solution