The displacement y of a particle periodic motion is given by
y=4cos(12t)sin(1000t)
This expression may be considered as a result of the superposition of
two
three
four
five
The correct Answer is:B
y=42[2cos2(t2)]sin(1000t)
or y=2(1+cost)sin1000t
or t = 2 sin 1000 t + 2 sin 1000 t cos t<br>or y = 2 sin 1000 t + sin (1001 t) + sin (999 t)
So , the given the expression is a result of the superposition of three independent harmonic motions .
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Multiple26videos
SUPERPOSITION AND STANDING WAVES
- BOOK - CENGAGE PHYSICSCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Assertion - Reasoning6videos
SUPERPOSITION AND STANDING WAVES
- BOOK - CENGAGE PHYSICSCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Subjective24videos
SUPERPOSITION AND STANDING WAVES
- BOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
- BOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - 241videos
THERMODYNAMICS
Similar Questions
Knowledge Check
- Question 1 - Select One
The displacement y of a particle executing periodic motion is given by y=4cos2(12t)sin(1000t)
This expression may be considered to be a result of the superposition ofA(a) twoB( b ) threeC( c ) fourD(d) five - Question 2 - Select One
The displacement of a particle in a periodic motion is given by y=4cos2(t2)sin(1000t). This displacement may be considered as the result of superposition of n independent harmonic oscillations. Here n is
A1B2C3D4 - Question 3 - Select One
The displacement x of a particle in a straight line motion is given by x=1−t−t2. The correct representation of the motion is
A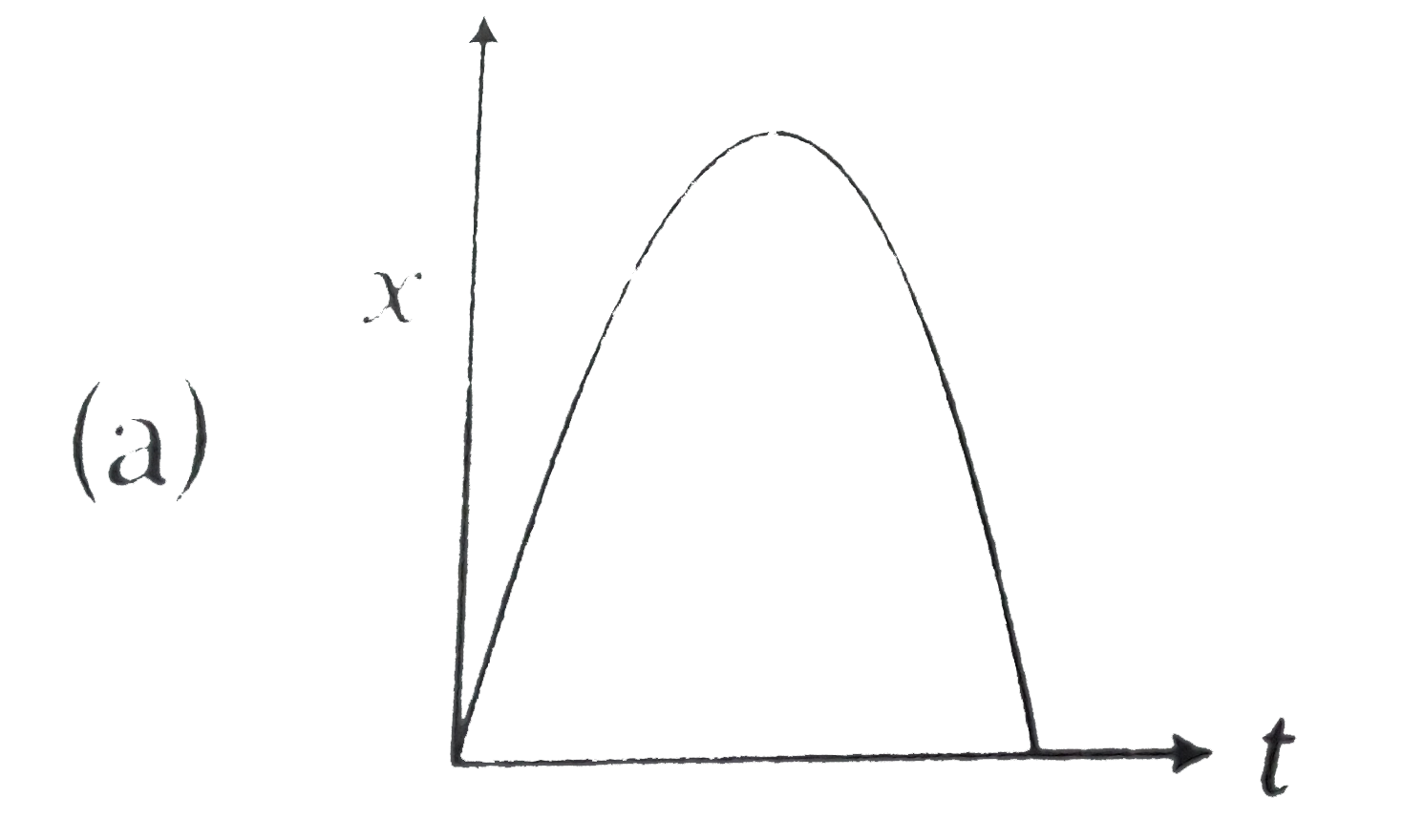 B
B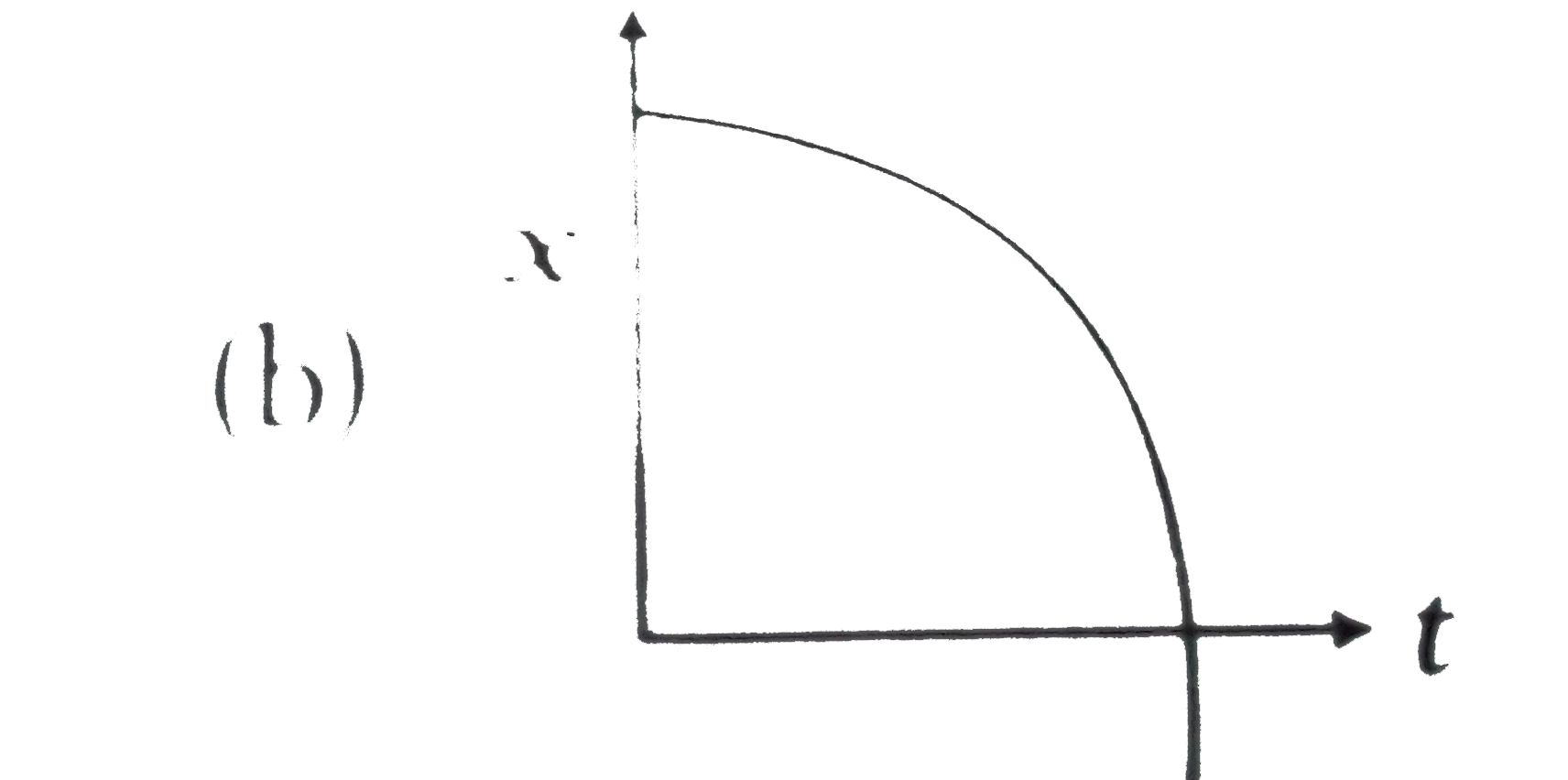 C
C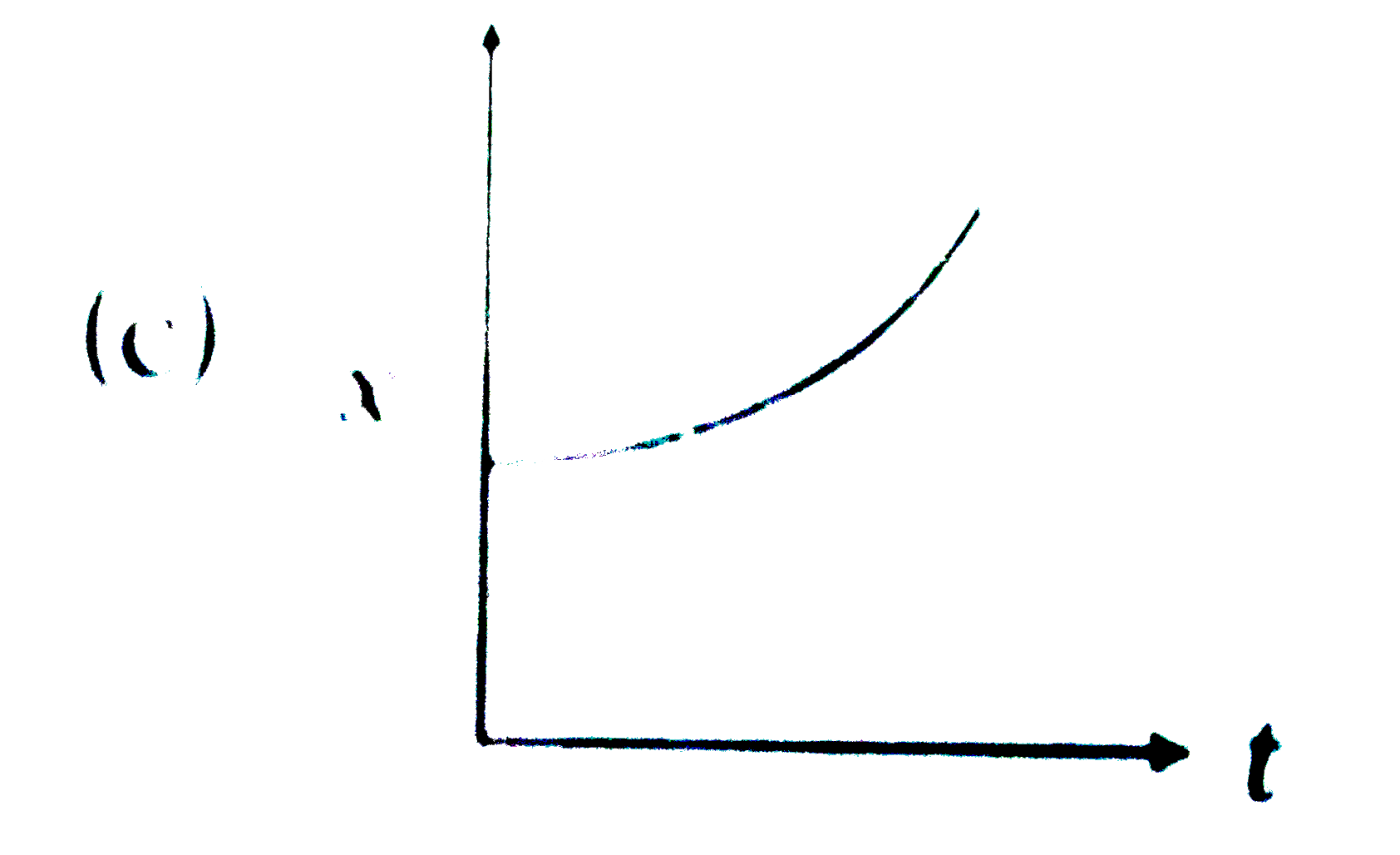 D
D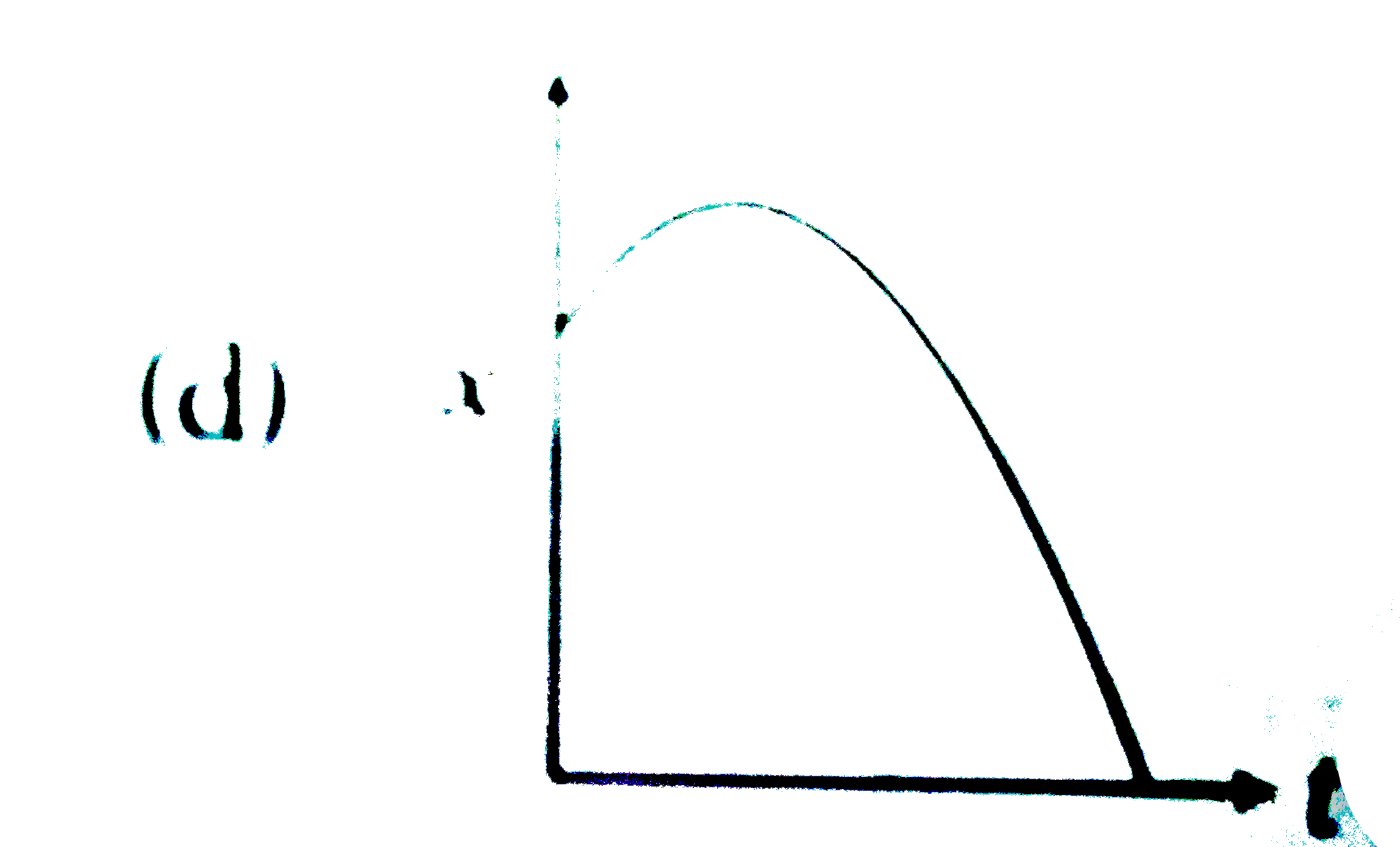
The displacement of a particle is given by x=3sin(5πt)+4cos(5πt). The amplitude of particle is
View SolutionThe displacement of a particle moving in S.H.M. at any instant is given by y=asinωt . The accelreation after time t=T4 os
View SolutionThe displacement of a particle is given at time t, by:
x=Asin(−2ωt)+Bsin2ωt Then,View SolutionThe displacement of a particle executing SHM is given by
Y=5 sin (4t+π3)
If T is the time period and the mass of the particle is 2g, the kinetic energy of the particle When t=T4 is given by-View SolutionThe displacement of a particle ( in meter ) from its mean position is given by the equation y=0.2(cos2πt2−sin2πt2), The motion of the above particle is
View Solution

