An open pipe is in resonance in $2 n d$ harmonic with frequency $f_{1}$ . Now one end of the tube is closed and frequency is increased to $f_{2}$ such that the resonance again ocuurs in $n t h$ harmonic. Choose the correct option

A

$n = 3, f_{2} = \frac{3}{4} f_{1}$

B

$n = 3, f_{2} = \frac{5}{4} f_{1}$

C

$n = 5, f_{2} = \frac{3}{4} f_{1}$

D

$n = 5, f_{2} = \frac{5}{4} f_{1}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

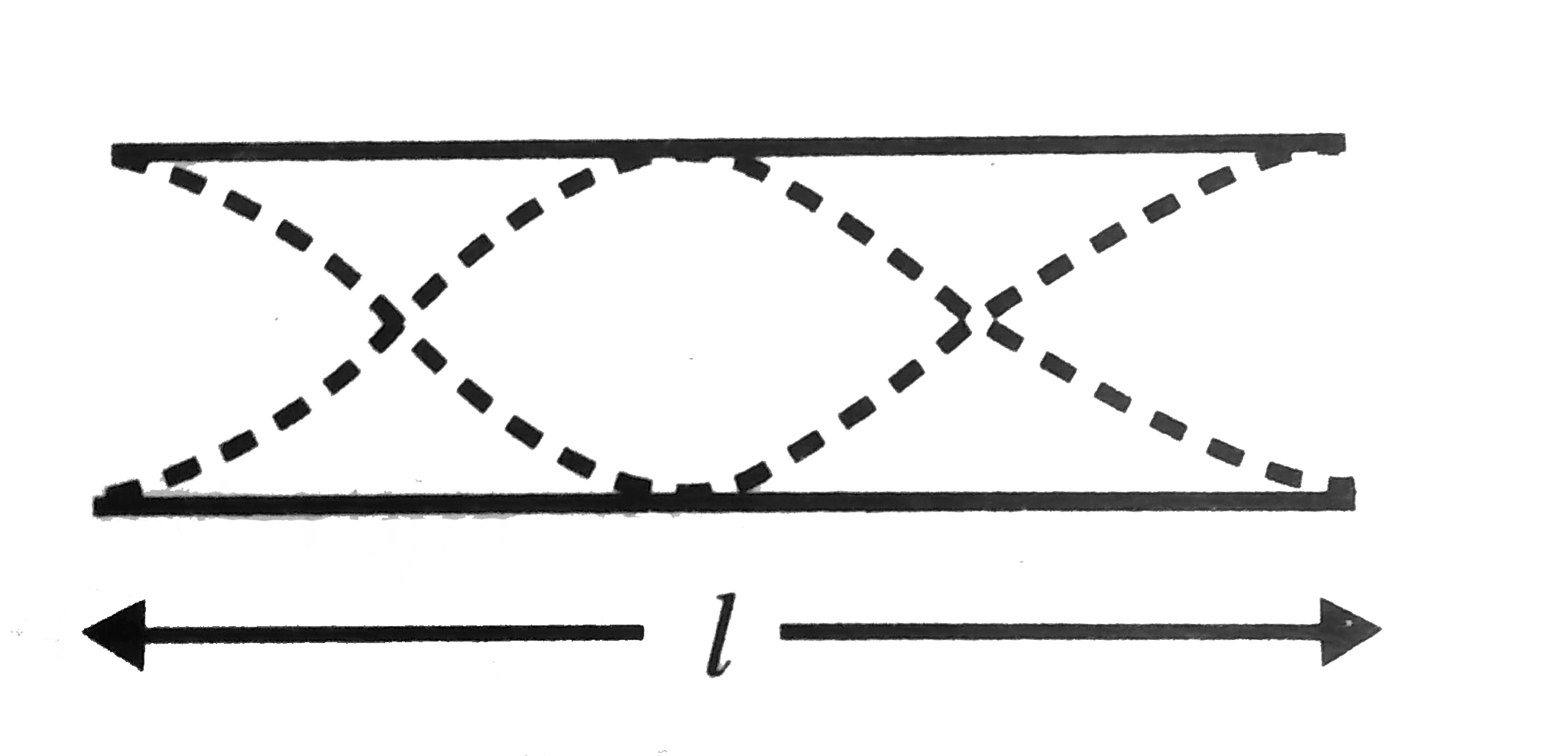
$λ = l$
$∴ f_{1} = \frac{v}{λ} = \frac{v}{l}$

$λ = \frac{4 l}{n}$
$∴ f_{2} = \frac{v}{λ} = \frac{n v}{4 l}$ …(ii)
Here $n$ is an odd number
$f_{2} = \frac{n}{4} f_{1}$
From Eqs. (i) and (ii), we get
For the first resonance
$n = 5$ ,
$f_{2} = \frac{5}{4} f_{1}$
Given $f_{2} > f_{1}$ .

|

Updated on:21/07/2023

Class 11 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
An open pipe is in resonance in its 2nd harmonic with tuning fork of frequency $f_{1}$ . Now it is closed at one end. If the frequency of the tuning fork is increased slowly from $f_{1}$ then again a resonance is obtained with a frequency $f_{2}$ . If in this case the pipe vibrates nth harmonics then
A $n = 3, f_{2} = \frac{3}{4} f_{1}$
B $n = 3, f_{2} = \frac{5}{4} f_{1}$
C $n = 5, f_{2} = \frac{5}{4} f_{1}$
D $n = 5, f_{2} = \frac{3}{4} f_{1}$
Question 2 - Select One
An open pipe is resonance is its $2^{n d}$ harmonic with tuning fork of freqency $f_{1}$ . Now it is closed at one end. If the frequency of the tuning fork is increases slowly from $f_{1}$ , then agaain a resonance is obtained with $a_{1}$ frequency $f_{2}$ . if in this case the pipe vibrates $n^{t h}$ harmonics, then
A $n = 3, f_{2} = \frac{3}{4} f_{1}$
B $n = 3, f_{2} = \frac{5}{4} f_{1}$
C $n = 5, f_{2} = \frac{5}{4} f_{1}$
D $n = 5, f_{2} = \frac{3}{4} f_{1}$
Question 3 - Select One
An open organ pipe of length L resonates at fundamental frequency with closed organ pipe. Find the length of closed organ pipe.
A $2 L$
B $L / 2$
C $L \sqrt{2}$
D $L \sqrt{3} / 2$

CENGAGE PHYSICS-ARCHIVES 2 VOLUME 6-Single Correct

Home
Ask Doubt
Profile