Based on $V S E P R$ theory the number of $90^{\circ} F - B r - F$ angles in a molecules of $B r F_{5}$ is_____.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:8

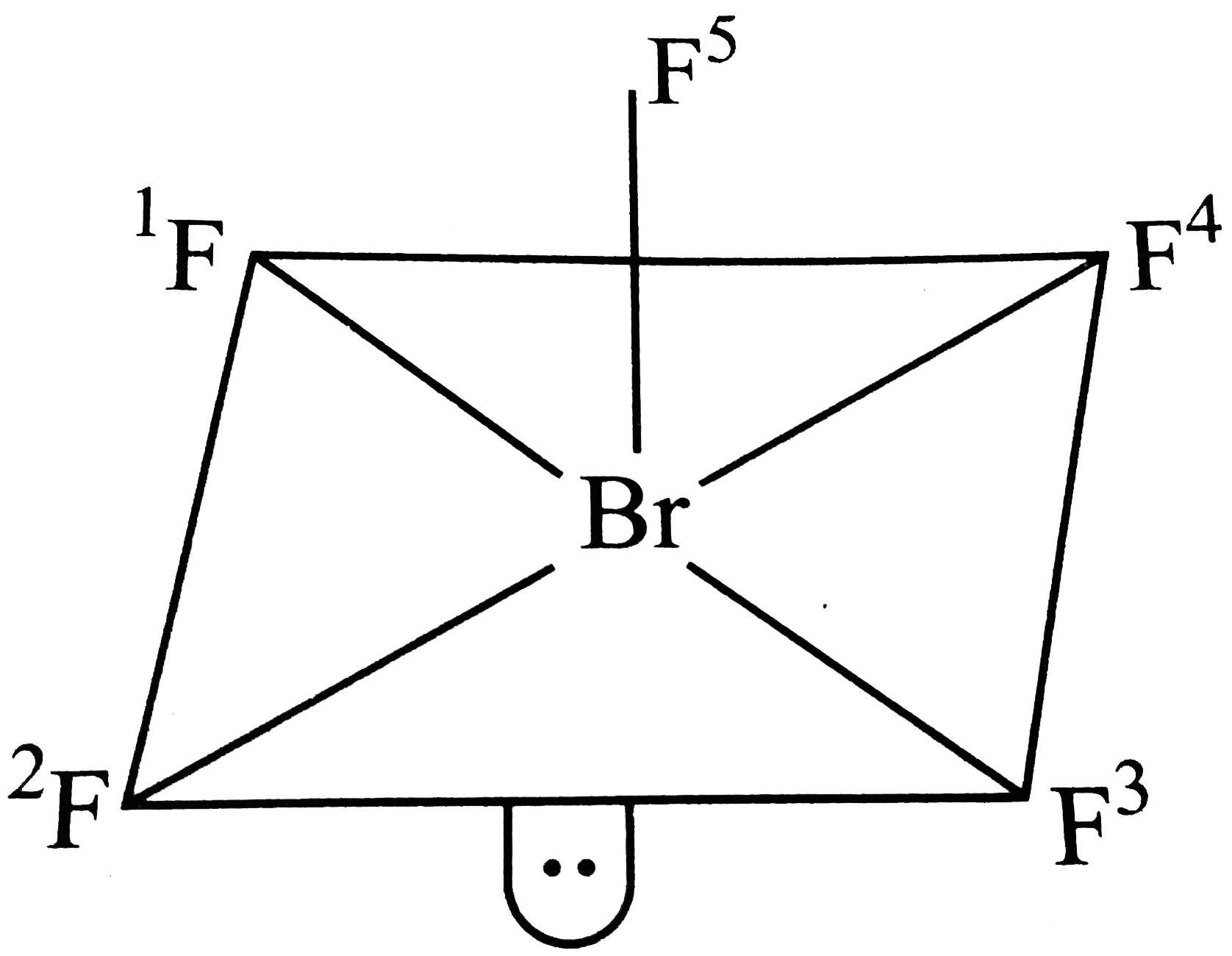
Hybridisation of Br in $b r F_{5} = \frac{1}{2} (7 + 5) = 6 = s p^{3} d^{2}$ Geometry $= O H$
Due to one lp of $e^{-'} s$ it has square pyrmidal shape
It has eight $(F - B r - F)$ bonds which are at $90^{\circ}$ There are
(1) $F^{1} - B r - F^{2}$ (2) $F^{2} - B r - F^{3}$ (3) $F^{3} - B r - F^{4}$
(4) $F^{4} - B r - F^{1}$ (5) $F^{1} - B r - F^{5}$ (6) $F^{5} - B r - F^{4}$
(7) $F^{5} - B r - F^{3}$ (8) $F^{5} - B r - F^{2}$
.

|

Updated on:21/07/2023

Class 11 CHEMISTRY CHEMICAL BONDING AND MOLECULAR STRUCTURE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Based on VSEPR theory, the number of 90 degree F-Br-F angles in $B r F_{5},$ is
A0
B1
C2
D3
Question 2 - Select One
F-S-F bond angles in $S F_{6}$ molecule are _________.
A $180^{\circ} and 90^{\circ}$
B $60^{\circ} and 90^{\circ}$
C $180^{\circ} and 60^{\circ}$
D $120^{\circ} and 90^{\circ}$

CENGAGE CHEMISTRY-CHEMICAL BONDING AND MOLECULAR STRUCTURE-Archives Integer

Home
Ask Doubt
Profile