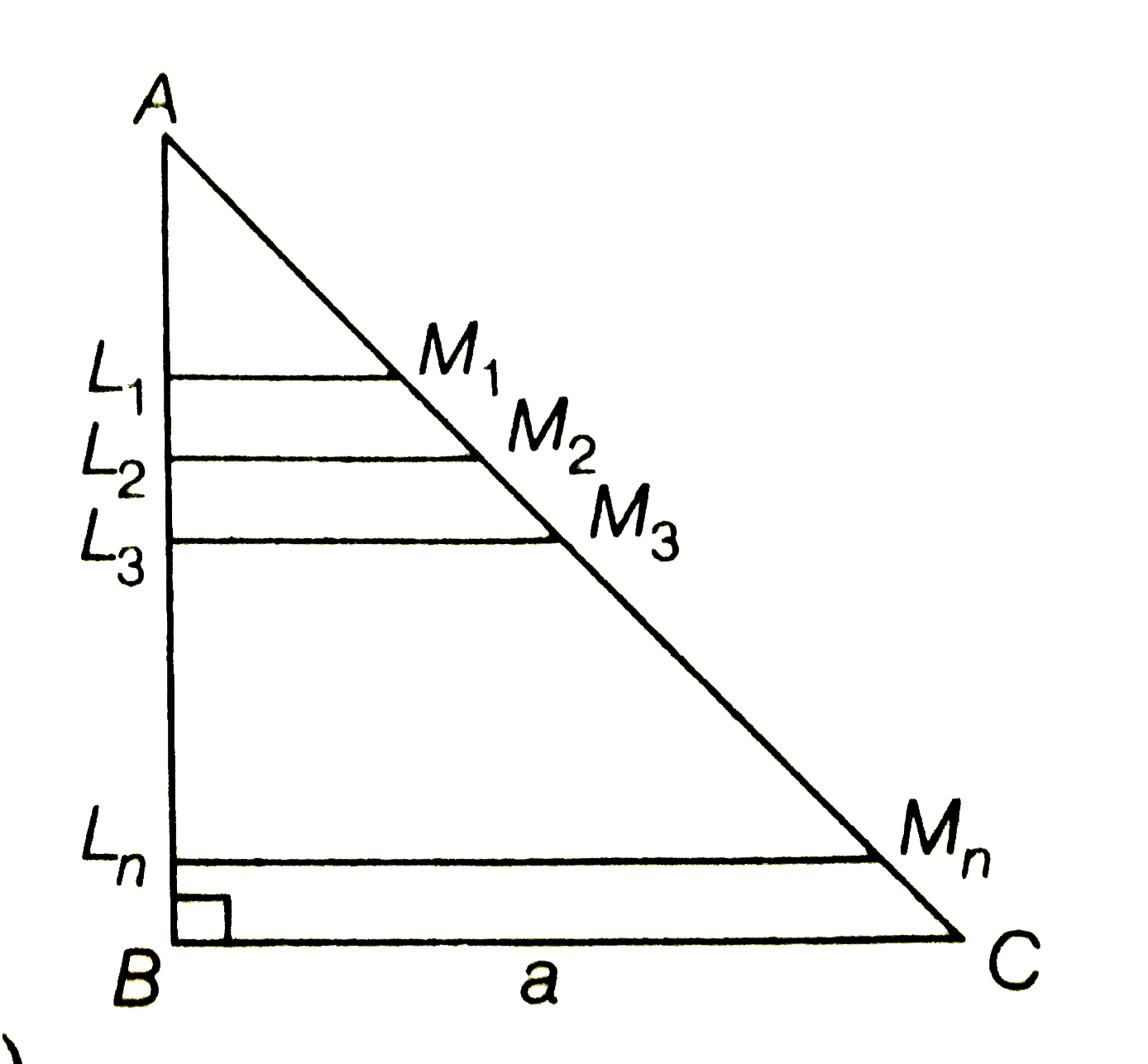
ABC is a right angled triangle in which $∠ B = 90^{\circ}$ and BC=a. If n points $L_{1}, L_{2}, \dots\dots., L_{n}$ on AB are such that AB is divided in $n + 1$ equal parts and $L_{1} M_{1}, L_{2} M_{2}, ......, L_{n} M_{n}$ are line segments parallel to BC and $M_{1}, M_{2}, M_{3}, ......, M_{n}$ are on AC, the sum of the lenghts of $L_{1} M_{1}, L_{2} M_{2}, ......, L_{n} M_{n}$ is

A

$\frac{n (n + 1)}{(2)}$

B

$\frac{a (n - 1)}{2}$

C

$\frac{a n}{2}$

D

Impossible to find from the given data

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

$∴ \frac{A L_{1}}{A B} = \frac{L_{1} M_{1}}{B C} \Rightarrow L_{1} M_{1} = \frac{a}{n + 1}$
Similarly, $L_{2} M_{2} = \frac{2 a}{n + 1}$
$L_{3} M_{3} = \frac{3 a}{n + 1}$
$⋮ ⋮ ⋮$
$L_{n} M_{n} = \frac{n a}{n + 1}$
$L_{1} M_{1} + L_{2} M_{2} + \dots. + L_{n} M_{n}$
$= \frac{a}{(n + 1)} (1 + 2 + 3 + ..... + n)$
$= \frac{a}{(n + 1)} \cdot \frac{n (n + 1)}{2} = \frac{n a}{2}$

|

Updated on:21/07/2023

Class 12 MATHS SEQUENCES AND SERIES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
ABC is a right-angled triangle in which $∠ B = 90^{\circ} and B C = a .$ If n points $L_{1}, L_{2}, \dots, L_{n}$ on AB is divided in n+1 equal parts and $L_{1} M_{1}, L_{2} M_{2}, \dots, L_{n} M_{n}$ are line segments paralllel to BC and $M_{1}, M_{2}, \dots ., M_{n}$ are on AC, then the sum of the lengths of $L_{1} M_{1}, L_{2} M_{2}, ..., L_{n} M_{n}$ is
A $\frac{a (n + 1)}{2}$
B $\frac{a (n - 1)}{2}$
C $\frac{a n}{2}$
Dnone of these
Question 2 - Select One
If $L_{1} = (2.02 \pm 0.01) m$ and $L_{2} = (1.02 \pm 0.01) m$ then $L_{1} + 2 L_{2}$ is (in m)
A $\frac{1}{2} a {(a - 1)}^{2}$
B $\frac{1}{2} a (a - 1) (4 a - 1)$
C $\frac{1}{2} (a - 1) (2 a - 1) (4 a - 1)$
DNone of these
Question 3 - Select One
Two lines with direction cosines $l_{1}, m_{1}, n_{1} and l_{2}, m_{2}, n_{2}$ are at right angle of
A $l_{1} l_{2} - m_{1} m_{2} - n_{1} n_{2} = 0$
B $l_{1} l_{2} + m_{1} m_{2} + n_{1} n_{2} = 0$
C $l_{2} = l_{2}, m_{1} = m_{2}, n_{1} = n_{2}$
D $\frac{l_{1}}{l_{2}} = \frac{m_{1}}{m_{2}} = \frac{n_{1}}{n_{2}}$

ARIHANT MATHS-SEQUENCES AND SERIES-Exercise (Single Option Correct Type Questions)

Home
Ask Doubt
Profile