A ball is projected upwards from a height h above the surface of the earth with velocity v. The time at which the ball strikes the ground is
vg+2hg√2
vg[1−√1+2hg]
vg[1+√1+2ghv2]
vg[1+√v2+2hh]
The correct Answer is:C
To find the time at which the ball strikes the ground after being projected upwards from a height h with an initial velocity v, we can use the equations of motion. Here’s a step-by-step solution:
Step 1: Identify the known quantities
- Initial height h
- Initial velocity v
- Acceleration due to gravity g (acting downward)
Step 2: Set up the equation of motion
We will use the second equation of motion:
S=Ut+12at2
where:
- S is the displacement (which will be −h when the ball hits the ground),
- U is the initial velocity v,
- a is the acceleration −g (since it is acting downward),
- t is the time of flight.
Step 3: Substitute the known values into the equation
The equation becomes:
−h=vt−12gt2
Rearranging gives:
12gt2−vt−h=0
Step 4: Rearrange into standard quadratic form
This is a standard quadratic equation of the form at2+bt+c=0:
12gt2−vt−h=0
where:
- a=12g,
- b=−v,
- c=−h.
Step 5: Apply the quadratic formula
The quadratic formula is given by:
t=−b±√b2−4ac2a
Substituting the values of a, b, and c:
t=−(−v)±√(−v)2−4⋅12g⋅(−h)2⋅12g
This simplifies to:
t=v±√v2+2ghg
Step 6: Determine the valid solution
Since time cannot be negative, we take the positive root:
t=v+√v2+2ghg
Final Answer
Thus, the time at which the ball strikes the ground is:
t=v+√v2+2ghg
- Initial height h
- Initial velocity v
- Acceleration due to gravity g (acting downward)
We will use the second equation of motion:
S=Ut+12at2
where:
- S is the displacement (which will be −h when the ball hits the ground),
- U is the initial velocity v,
- a is the acceleration −g (since it is acting downward),
- t is the time of flight.
The equation becomes:
−h=vt−12gt2
Rearranging gives:
12gt2−vt−h=0
This is a standard quadratic equation of the form at2+bt+c=0:
12gt2−vt−h=0
where:
- a=12g,
- b=−v,
- c=−h.
The quadratic formula is given by:
t=−b±√b2−4ac2a
Substituting the values of a, b, and c:
t=−(−v)±√(−v)2−4⋅12g⋅(−h)2⋅12g
This simplifies to:
t=v±√v2+2ghg
Since time cannot be negative, we take the positive root:
t=v+√v2+2ghg
Thus, the time at which the ball strikes the ground is:
t=v+√v2+2ghg
Similar Questions
A body is projected vertically upward from the surface of the earth with escape velocity. Calculate the time in which it will be at a height (measured from the surface of the arth) 8 time the radius of the earth (R). Acceleration due to gravity on the surface of the earth is g.
View SolutionAn object is projected vertically upward from the surface of the earth of mass M with a velocity such that the maximum height reached is eight times the radius R of the earth. Calculate:
(i) the initial speed of projection
(ii) the speed at half the maximum height.
View Solution
Knowledge Check
A body is projected vertically upward from the surface of the earth, then the velocity-time graph is:-
A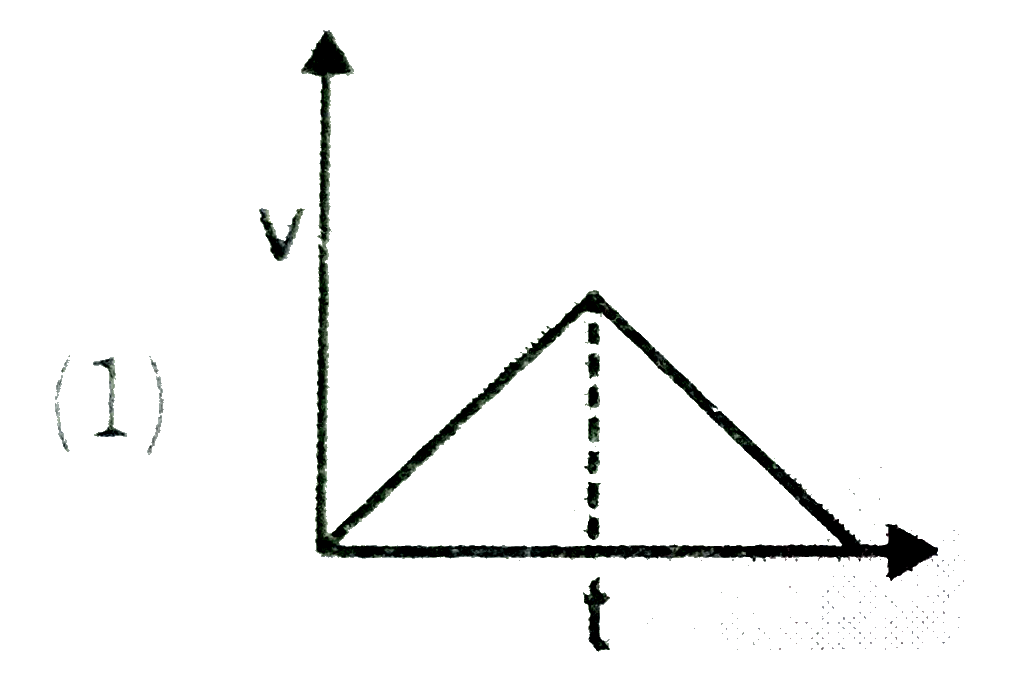 B
B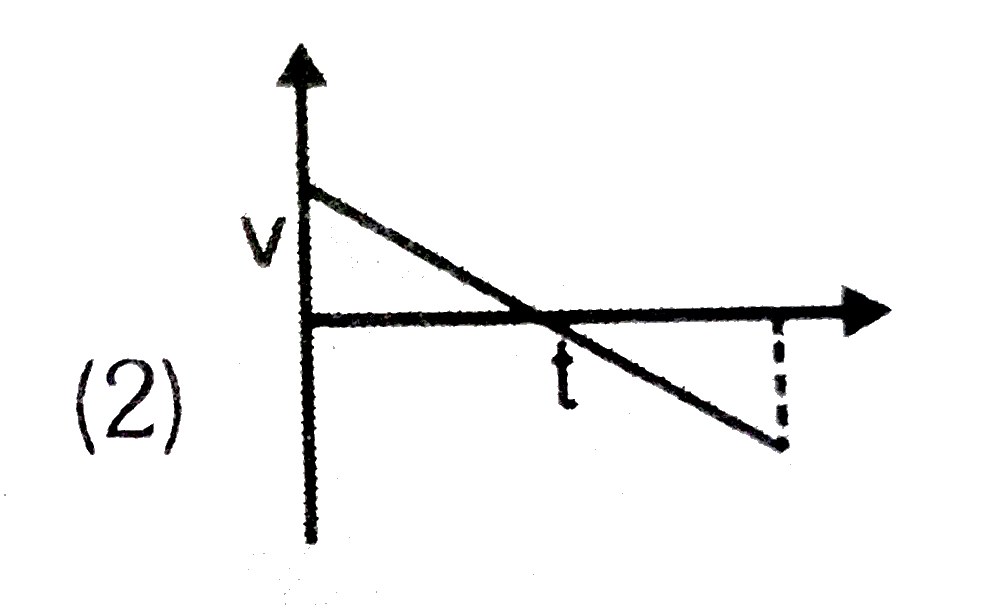 C
C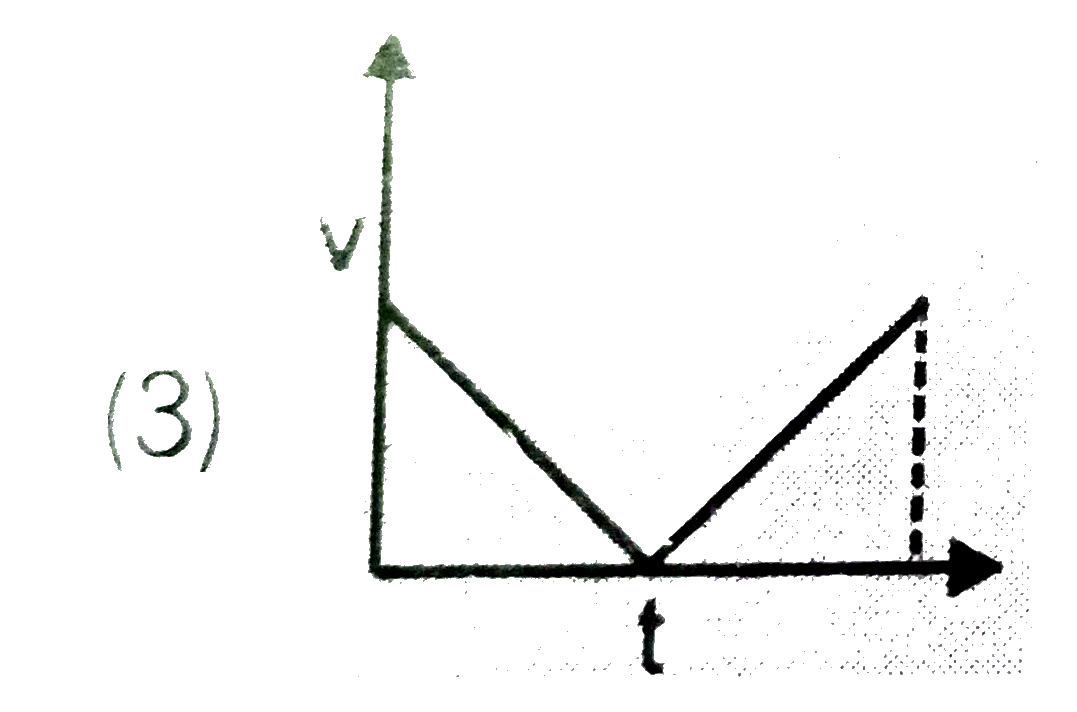 D
D
A ball is thrown straight upward with a speed v from a point h meter above the ground. The time taken for the ball to strike the ground is
Avg[1+√1+2hgv2]Bvg[1−√1−2hgv2]Cvg[1−√1+2hgv2]Dvg[2+2hgv2]A ball is thrown horizontally with a speed of 20m/s from the top of a tower of height 100m
velocity with which the ball strikes the ground is .A20√6m/s at angle tan−10(√7) below the horizontalB20√6m/s at an angle tan−1(√6) below the horizontalC20√6m/s at an angle tan−1(√5) below the horizontalD10√6m/s at an angle tan−1(√5) below the horizontal
An objects is projected vertically upwards from the surface of the earth with a velocity 3 times the escape velocity ve from earth's surface. What will be its final velocity after escape from the earth's gravitational pull ?
View SolutionA ball is thrown vertically upwards from the top of tower of height h with velocity v . The ball strikes the ground after time.
View SolutionA ball is thrown vertically upward with a velocity u from the top of a tower. If it strikes the ground with velocity 3u, the time taken by the ball to reach the ground is
View SolutionA ball is dropped from a height h above ground. Neglect the air resistance, its velocity (v) varies with its height (y) above the ground as :-
View SolutionA ball is thrown upwards with a speed u from a height h above the ground.The time taken by the ball to hit the ground is
View Solution
