Points A and C are on the horizontal ground and A and B are in same vertical plane at a distance of 1500m. Simultaneously bullets are fired from A,Bll and C and they collide at O. The bullets at B is fired at an angle of 30∘with horizontal towards the ground iat velocity 100m/s. the bullet at C is projected vertically upwards at velocity of 100m/s. the bullet projected from A reaches its maximum height at O.
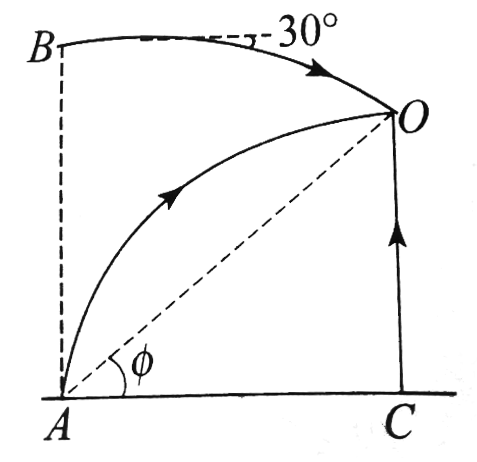
Find the time in which bullets will collide (seconds ):
The correct Answer is:A
Let us be the velocity of bass A is 2.0 m
2.0=(usinθ)t−12>2
For bullet C vertical distance travelled =usin30∘t+12> ..(i)
For bullet C, vertical distance travelled
d=u)t-(1)/(2)gt^(2)<br>Fromequation(i)and(ii),<br>usin30^@t+u^()t=1500
50t+100t=1500 which gives t=10 sec
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - CENGAGE PHYSICS DPPEXERCISE - single correct type14videos
CENGAGE PHYSICS DPP
- BOOK - CENGAGE PHYSICSCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type51videos
CENGAGE PHYSICS DPP
- BOOK - CENGAGE PHYSICSCHAPTER - CENGAGE PHYSICS DPPEXERCISE - Fill in the blanks type26videos
CENGAGE PHYSICS DPP
- BOOK - CENGAGE PHYSICSCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer5videos
CAPACITOR AND CAPACITANCE
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASS CONVERSATION OF MOMENTUM AND COLLISIONEXERCISE - Question Bank38videos
CENTRE OF MASS CONVERSATION OF MOMENTUM AND COLLISION
Similar Questions
Points A and C are on the horizontal ground and A and B are in same vertical plane at a distance of 1500m. Simultaneously bullets are fired from A,Bll and C and they collide at O. The bullets at B is fired at an angle of 30∘with horizontal towards the ground iat velocity 100m/s. the bullet at C is projected vertically upwards at velocity of 100m/s. the bullet projected from A reaches its maximum height at O.
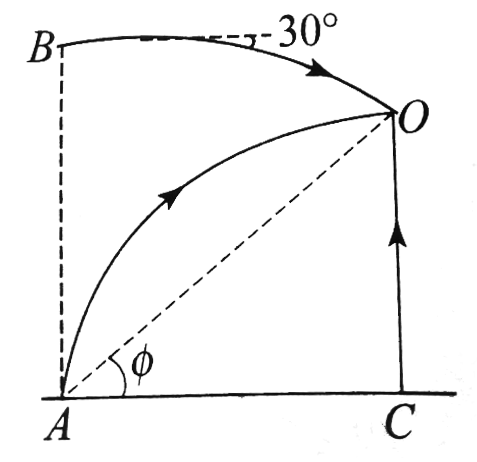
Find the velocity of bullet at A:View SolutionPoints A and C are on the horizontal ground and A and B are in same vertical plane at a distance of 1500m. Simultaneously bullets are fired from A,Bll and C and they collide at O. The bullets at B is fired at an angle of 30∘with horizontal towards the ground iat velocity 100m/s. the bullet at C is projected vertically upwards at velocity of 100m/s. the bullet projected from A reaches its maximum height at O.

Find the elevation angle ∠θ=∠OAC:View Solution
Knowledge Check
- Question 1 - Select One
A body is projected at an angle of 60∘ with ground. It covers a horizontal distance of 100m. If the same body is projected at 60∘ with vertical with same velocity, the new range is
A50mB100mC200mD150m - Question 2 - Select One
A bullet of mass 20gm is fired from a riffle of mass 8 kg with a velocity of 100m/s. The velocity of recoil of the rifle is
A0.25m/sB25m/sC2.5m/sD250m/s - Question 3 - Select One
A bullet of mass m is fired at angle θ with the vertical. The bullet returns to the ground in time t. The total change of momentum equals
AmgtB2mgtCmgtD2mgt
In the given figure points A and C are on the horizontal ground & A and B are in same vertical plane. Simultaneously bullets are fired from A, B and C and they collide at D. The bullet at B is fired horizontally with speed of 725km/hr and the bullet at C is projected vertically upward at velocity of 545km/hr. Find velocity of the bullet projected from A in m/s.
 View Solution
View SolutionA particle is projected vertically upwards from ground with velocity 10 m/s. Find the time taken by it to reach at the highest point ?
View SolutionA bullet fired at an angle of 60∘ with the vertical his the levelled ground at a distance of 200 m . Find the distance at which the bullet will hit the ground when fired at angle of 30∘. (with same speed).
View SolutionA bullet fired at an angle of 60∘ with the vertical hits the ground at a distance of 2 km. Calculate the distance at which the bullet will hit the ground when fired at an angle of 45∘, assuming the speed to be the same.
View SolutionA bullet fired at an angle of 60∘ with the vertical hits the ground at a distance of 2 km. Calculate the distance at which the bullet will hit the ground when fired at an angle of 45∘,assuming the speed to be the same.
View Solution

