A body B lies on a smooth horizontal table and another body A is placed on B. The coefficient of friction between A and B is μ. What acceleration given to B will cause slipping to occur between A and B
μg
gμ
μg
√μg
The correct Answer is:A
To solve the problem of determining the acceleration given to body B that will cause slipping to occur between bodies A and B, we can follow these steps:
1. Understanding the System:
- Body A is placed on top of body B, which is on a smooth horizontal table.
- The coefficient of friction between A and B is given as μ.
2. Applying Force to Body B:
- When we apply a force F to body B, both bodies A and B will start to accelerate. However, body A will experience a pseudo force due to the acceleration of body B.
3. Acceleration of the System:
- The total mass of the system (A + B) is \( M_A + M_B \).
- The acceleration \( a \) of the system when force \( F \) is applied can be expressed as:
\(
a = \frac{F}{M_A + M_B}
\)
4. Pseudo Force on Body A:
- As body B accelerates, body A experiences a pseudo force due to this acceleration. The pseudo force \( F_{pseudo} \) acting on body A is given by:
\(
F_{pseudo} = M_A \cdot a
\)
- Substituting the expression for acceleration:
\(
F_{pseudo} = M_A \cdot \frac{F}{M_A + M_B}
\)
5. Frictional Force:
- The frictional force \( F_{friction} \) that prevents slipping between A and B is given by:
\(
F_{friction} = \mu \cdot M_A \cdot g
\)
- Here, \( g \) is the acceleration due to gravity.
6. Condition for Slipping:
- Slipping will occur when the pseudo force exceeds the maximum static frictional force:
\(
M_A \cdot \frac{F}{M_A + M_B} > \mu \cdot M_A \cdot g
\)
7. Simplifying the Inequality:
- Dividing both sides by \( M_A \) (assuming \( M_A \neq 0 \)):
\(
\frac{F}{M_A + M_B} > \mu \cdot g
\)
- Rearranging gives:
\(
F > \mu \cdot g \cdot (M_A + M_B)
\)
8. Finding the Acceleration:
- The acceleration \( a_B \) of body B when the force \( F \) is applied can be expressed as:
\(
a_B = \frac{F}{M_B}
\)
- Therefore, substituting the expression for \( F \):
\(
a_B > \frac{\mu \cdot g \cdot (M_A + M_B)}{M_B}
\)
9. Final Expression:
- The minimum acceleration \( a_B \) required to cause slipping between A and B is:
\(
a_B = \mu \cdot g \cdot \frac{(M_A + M_B)}{M_B}
\)
- Body A is placed on top of body B, which is on a smooth horizontal table.
- The coefficient of friction between A and B is given as μ.
- When we apply a force F to body B, both bodies A and B will start to accelerate. However, body A will experience a pseudo force due to the acceleration of body B.
- The total mass of the system (A + B) is \( M_A + M_B \).
- The acceleration \( a \) of the system when force \( F \) is applied can be expressed as:
\(
a = \frac{F}{M_A + M_B}
\)
- As body B accelerates, body A experiences a pseudo force due to this acceleration. The pseudo force \( F_{pseudo} \) acting on body A is given by:
\(
F_{pseudo} = M_A \cdot a
\)
- Substituting the expression for acceleration:
\(
F_{pseudo} = M_A \cdot \frac{F}{M_A + M_B}
\)
- The frictional force \( F_{friction} \) that prevents slipping between A and B is given by:
\(
F_{friction} = \mu \cdot M_A \cdot g
\)
- Here, \( g \) is the acceleration due to gravity.
- Slipping will occur when the pseudo force exceeds the maximum static frictional force:
\(
M_A \cdot \frac{F}{M_A + M_B} > \mu \cdot M_A \cdot g
\)
- Dividing both sides by \( M_A \) (assuming \( M_A \neq 0 \)):
\(
\frac{F}{M_A + M_B} > \mu \cdot g
\)
- Rearranging gives:
\(
F > \mu \cdot g \cdot (M_A + M_B)
\)
- The acceleration \( a_B \) of body B when the force \( F \) is applied can be expressed as:
\(
a_B = \frac{F}{M_B}
\)
- Therefore, substituting the expression for \( F \):
\(
a_B > \frac{\mu \cdot g \cdot (M_A + M_B)}{M_B}
\)
- The minimum acceleration \( a_B \) required to cause slipping between A and B is:
\(
a_B = \mu \cdot g \cdot \frac{(M_A + M_B)}{M_B}
\)
Similar Questions
Two block A and B are connected to a spring (force constant k = 480 N/m) and placed on a horizontal surface. Another block C is placed on B. The coefficient of friction between the floor and block A is μ1=0.5, whereas there is no friction between B and the floor. Coefficient of friction between C and B is μ2=0.85. Masses of the blocks are MA=50kg,MB=28 kg and MC=2kg. The system is held at rest with spring compressed by x0=0.5m. After the system is released, find the maximum speed of block B during subsequent motion.
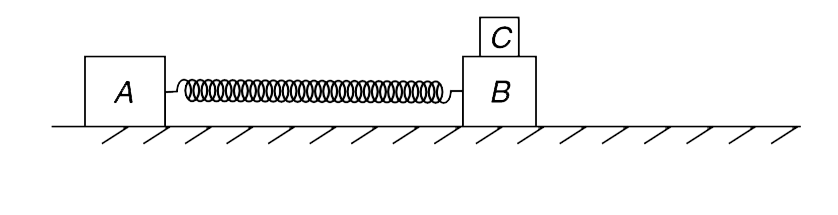
View SolutionA block of mass m slips on a rough horizontal table under the action of horiozontal force applied to it. The coefficient of friction between the block and the table is μ. The table does not move on the floor. Find the total frictional force aplied by the floor on the legs of the table. Do you need the friction coefficient between the table and the floor or the mass of the table ?
View Solution
Knowledge Check
If the coefficient of friction between A and B is μ, the maximum acceleration of the wedge A for which B will remain at rest with respect to the wedge is
 AμgBg(1+μ1−μ)Cg(1−μ1+μ)Dgμ
AμgBg(1+μ1−μ)Cg(1−μ1+μ)DgμA body of mass 2 kg is placed on rough horizontal plane. The coefficient of friction between body and plane is 0.2 Then,
 Abody will move in forward direction if F = 5 NBbody will be move in backward direction with acceleration 0.5m/s2 if force F = 3NCif F = 3N, then body will be in rest conditionDBoth a and c are correct
Abody will move in forward direction if F = 5 NBbody will be move in backward direction with acceleration 0.5m/s2 if force F = 3NCif F = 3N, then body will be in rest conditionDBoth a and c are correctBlock B rests on a smooth surface .The coefficient of static friction between A and B is μ=0.4 where F=30N then

Acceleration of upper block isA3/2ms−2B6/7ms−2C4/3ms−2D3/7ms−2
A block A of mass m kg lies on a block B of mass m kg. B in turn lies on smooth horizontal plane. The coefficient of friction between A and B is μ. Both the blocks are initially at rest. A horizontal force F is applied to lower block B at t = 0 till the lower block B undergoes a displacement of magnitude L. Match the statements in Table-1 with the results in Table-2.

View SolutionBlock B rests on a smooth surface .The coefficient of static friction between A and B is μ=0.4 where F=30N then
Acceleration of lower block is

View SolutionA body A of mass 1 kg rests on a smooth surface. Another body B of mass 0.2 kg is placed over A as shown. The coefficient of static friction between A and B is 0.15. B will begin to slide on A, if A is pulled with a force greater than -

View SolutionA uniform cylinder of mass M and radius R is placed on a rough horizontal board, which in turn is placed on a smooth surface. The coefficient of friction between the board and the cylinder is μ. If the board starts accelerating with constant acceleration a, as shown in the figure, then

View Solution
Two blocks A (1 kg) and B (2 kg) are connected by a string passing over a smooth pulley as shown in the figure. B rests on rough horizontal surface and A rest on B. The coefficient of friction between A and B is the same as that between B and the horizontal surface. The minimum horizontal force F required to move A to the left is 25 N. The coefficient of friction is:
View Solution
