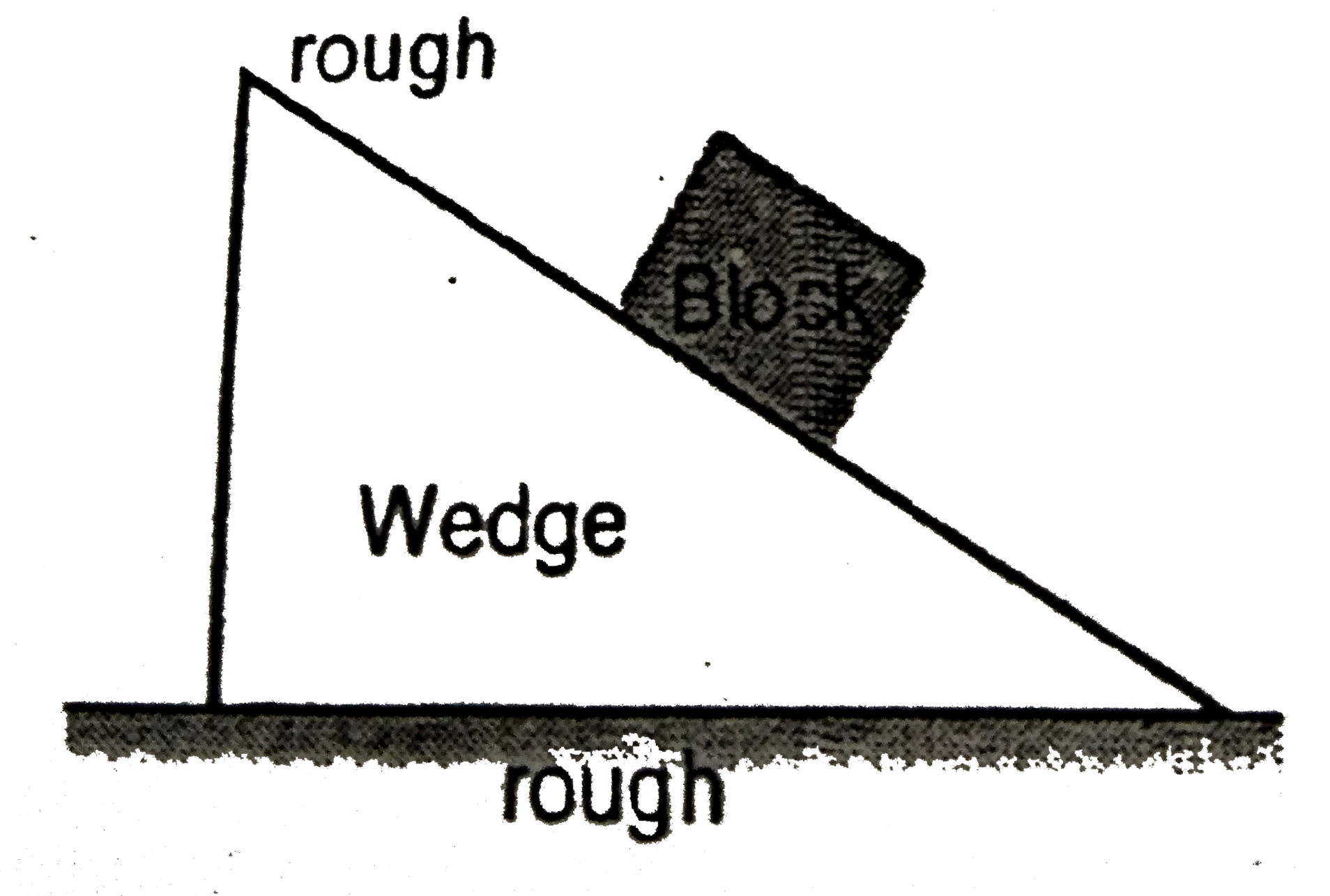
The minimum value of acceleration of wedge for which the block start sliding on the wedge, is:
g(cosθ+μsinθsinθ−μcosθ)
g(sinθ+μcosθcosθ−μsinθ)
g(sinθ−μcosθsinθ+μcosθ)
g(cosθ−μsinθsinθ+μcosθ)
The correct Answer is:B

Block will start siding if
macosθ≥mgsinθ+μ(mgcosθ+masinθ)
get a>g(sinθ+μcosθcosθ−μsinθ)
Similar Questions
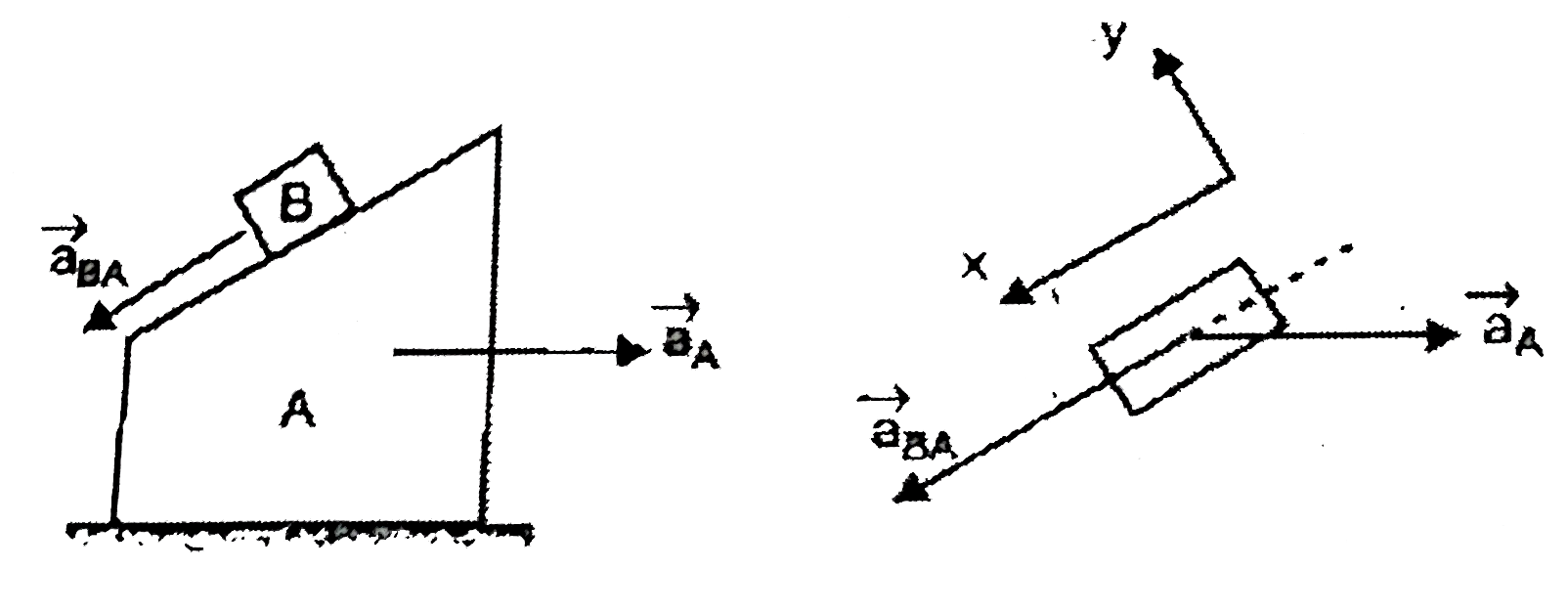
The block B starts from rest and slides on the wedge A which can move on a horizontal surface, Neglecting friction, determine (a) the acceleration of wedge, (b) the acceleration of the block relative to the wedge.
 View Solution
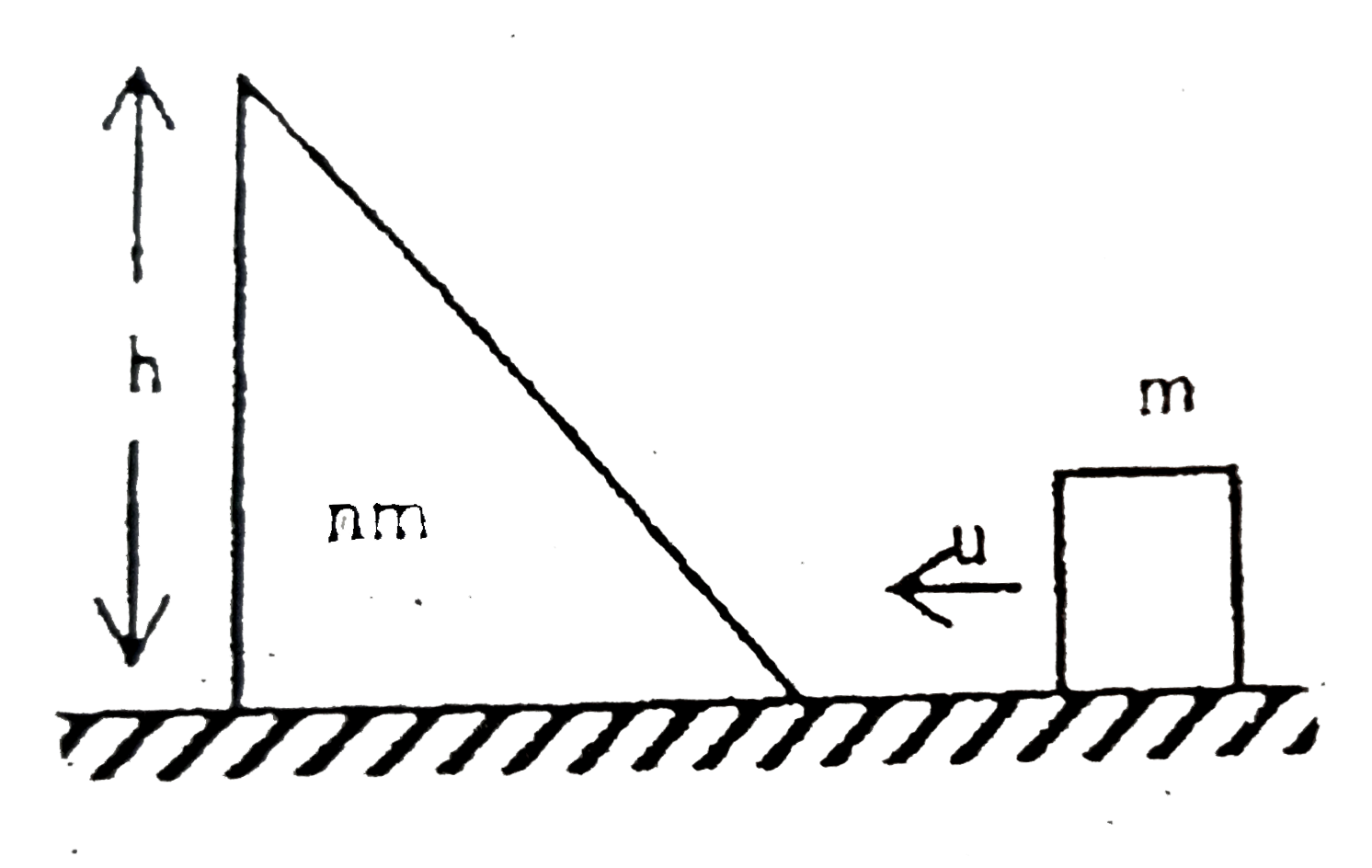
View SolutionA block of mass m is pushed towards a movable wedge of mass nm and height h, with a velocity u. All surfaces are smooth. The minimum value of u for which the block will reach the top of the wedge is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m is placed over the wedge as shown in figue Coefficent of frition μ is half the minimum value required to keep it in this postion.

what is the minimum value of accleration of wedge to keep the blok statinary with respect to the wedge in either of the four cases?
 Ag2√3B√3g4C√3g7Dg2√5
Ag2√3B√3g4C√3g7Dg2√5 - Question 2 - Select One
A block of mass m is placed at the top of a smooth wedge ABC. The wedge is rotated about an axis passing through C as shown in the figure - 3.81. The minimum value of angular speed ω such that the block does not slip on the wedge is :
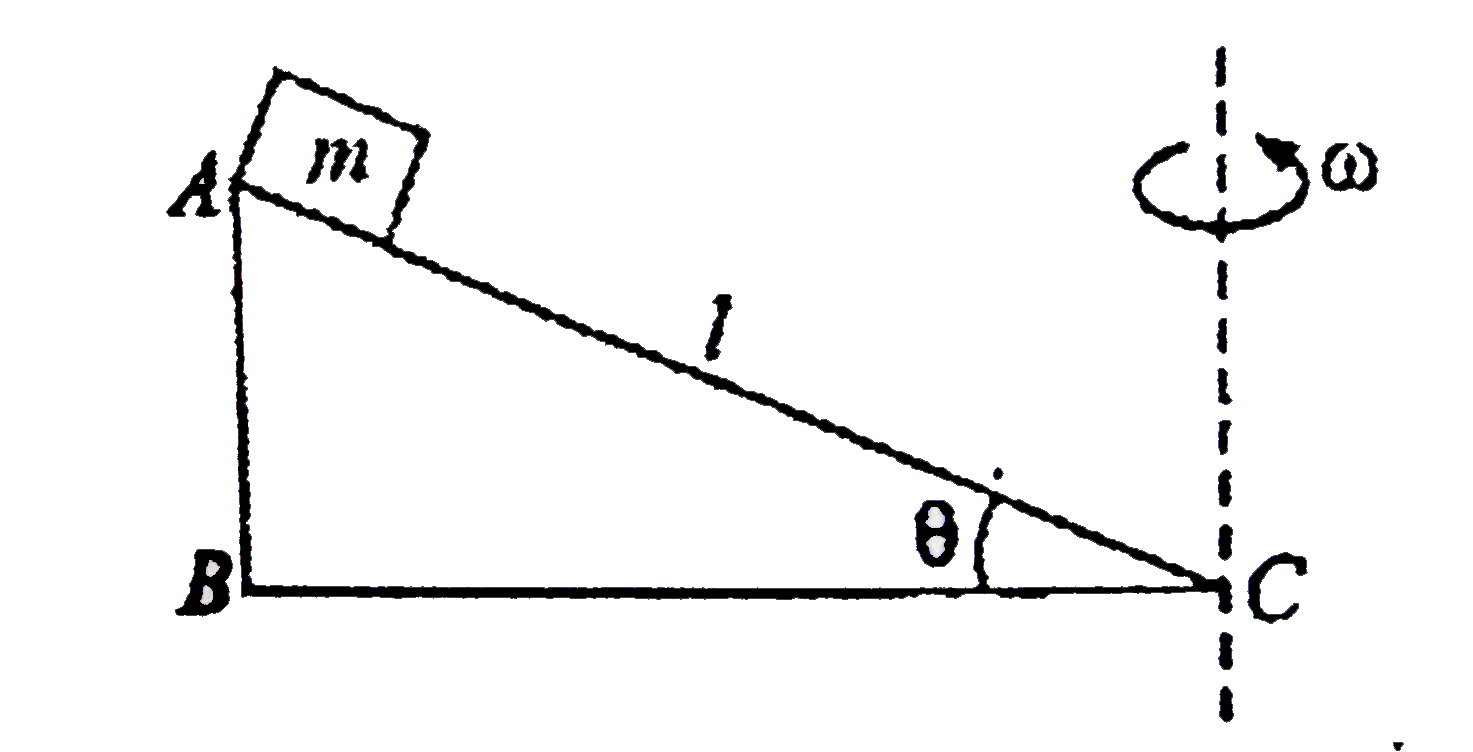 A⎛⎝√gsinθl⎞⎠secθB(√gl)cosθC(√glcosθ)cosθD√gsinθl
A⎛⎝√gsinθl⎞⎠secθB(√gl)cosθC(√glcosθ)cosθD√gsinθl - Question 3 - Select One
A block of mass m is pushed towards a movable wedge of mass nm and height h, with a velocity u. All surfaces are smooth. The minimum value of u for which the block will reach the top of the wedge is
 A√2ghB2nghC√2gh(1+1n)D√2gh(1−1n)
A√2ghB2nghC√2gh(1+1n)D√2gh(1−1n)
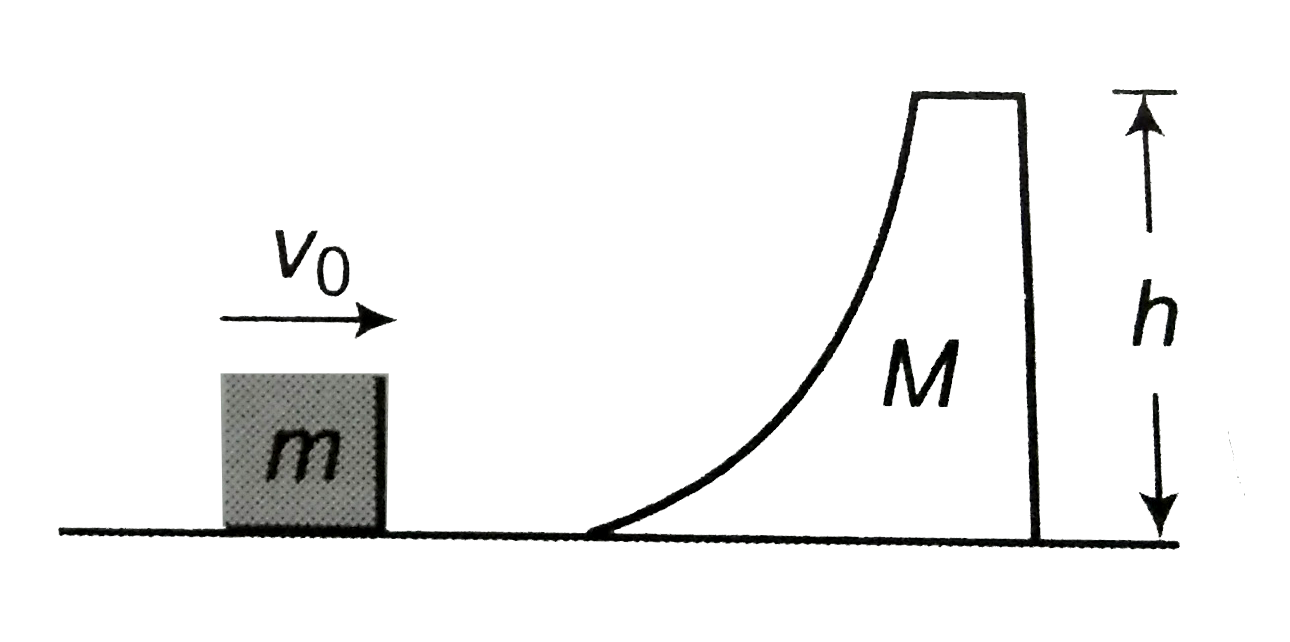
A block of mass m is pushed towards the movable wedge of mass M and height h, with a velocity v0. All surfaces are smooth . The minimum value of v0 for which the block will reach the top of the wedge is
 View Solution
View SolutionIf the coefficient of friction between A and B is μ, the maximum acceleration of the wedge A for which B will remain at rest with respect to the wedge is
 View Solution
View SolutionWhen a block is placed on a wedge as shown in figure, the block starts sliding down and the wedge also start sliding on ground. All surfaces are rough. The centre of mass of ( wedge + block ) system will move.
 View Solution
View SolutionA small block of mass m is pushed towards a movable wedge of mass ηm and height h with initial velocity u.All surface are smooth. The minimum value of u for which the block will reach the top of the wedge:
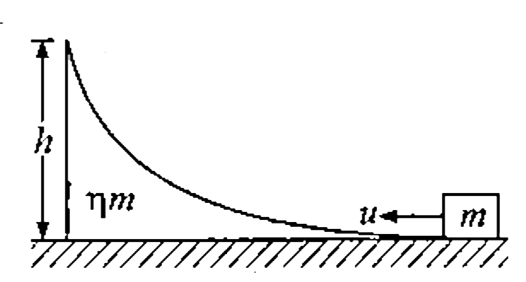 View Solution
View SolutionA small block of mass m is pushed towards a movable wedge of mass ηm and height h with initial velocity u.All surface are smooth. The minimum value of u for which the block will reach the top of the wedge:
 View Solution
View Solution

