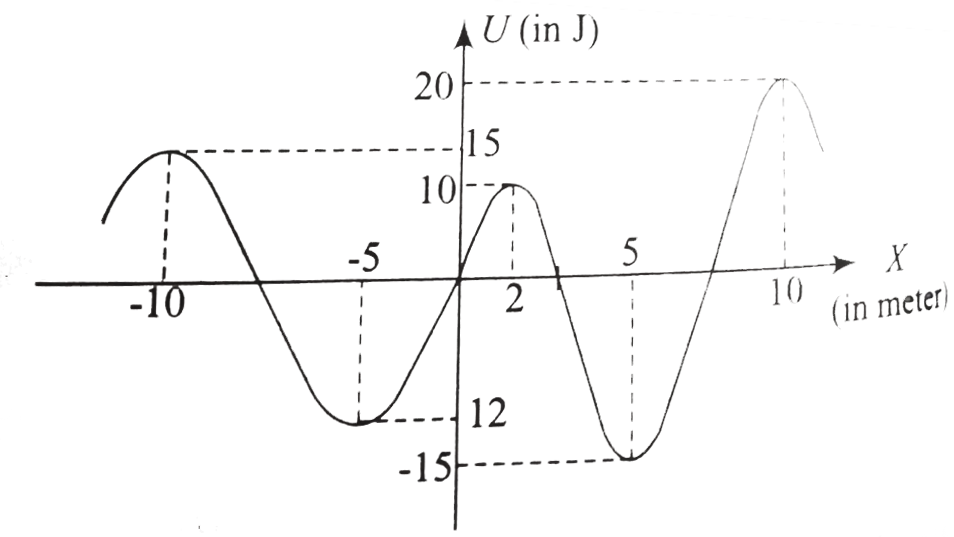
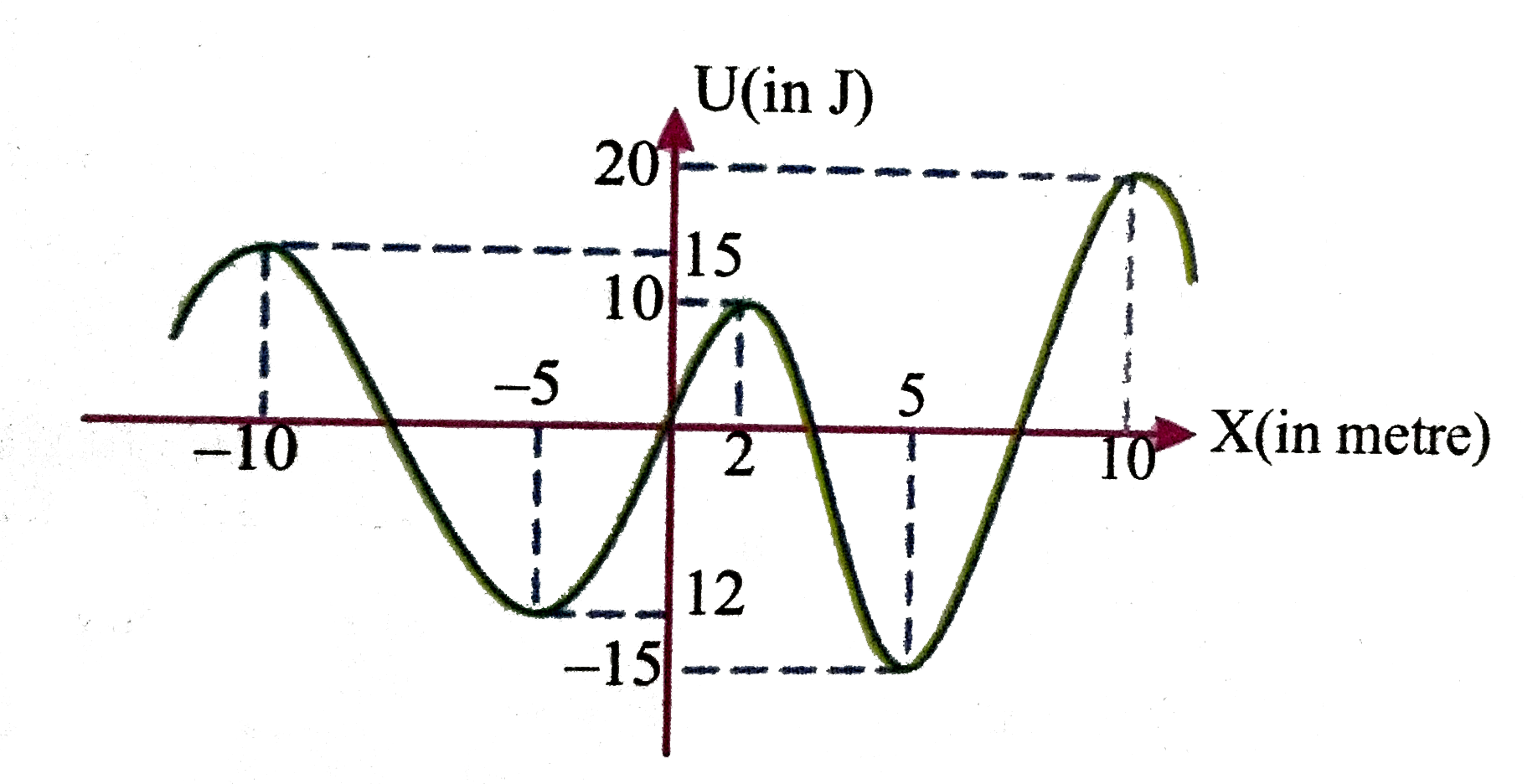
In the figure the variation of potential energy of a particle of mass m=2kg is represented w.r.t. its x-coordinate. The particle moves under the effect of this conservative force along the x-axis. Which of the following statements are correct about the particle:
If it is released at the origin it will move in negative x-axis
If it is released at x=2+△ where △→0 then its maximum speed will be 5ms and it will perform oscillatory motion
If initially x=−10m and →u=√6ˆims then it will cross x=10m
x=−5m and x=+5 m are unstable equilibrium positions of the particle.
The correct Answer is:A, B, C
If the particle is released at the origin, it will try to go in the direction of force. Here dudx is positive and hence force is negative, as a result it will move towards−vex-axis.
When the particle is released at x=2+△, it will reach the point of least possible potential energy (−15J) where it will have maximum kinetic energy.
12mv2max=25⇒vmax=5ms
The particle will now perform oscillatory motion between −15J≤U≤15J, because reaching U=+15J, the kinetic energy and hence speed becomes zero.
−15J≤U≤15J,U=+15J,
In (C ), Ei=Ui+ki=15+6=21J
At x=10m , Uf=20J⇒Kf=1J≠0⇒x=10m
⇒ the particle cross x=10m.
Similar Questions
In the figure, the variation of potential energy of a particle of mass m = 2kg is represented with respect to its x-coordinate. The particle moves under the effect of this conservative force along the X-axis.
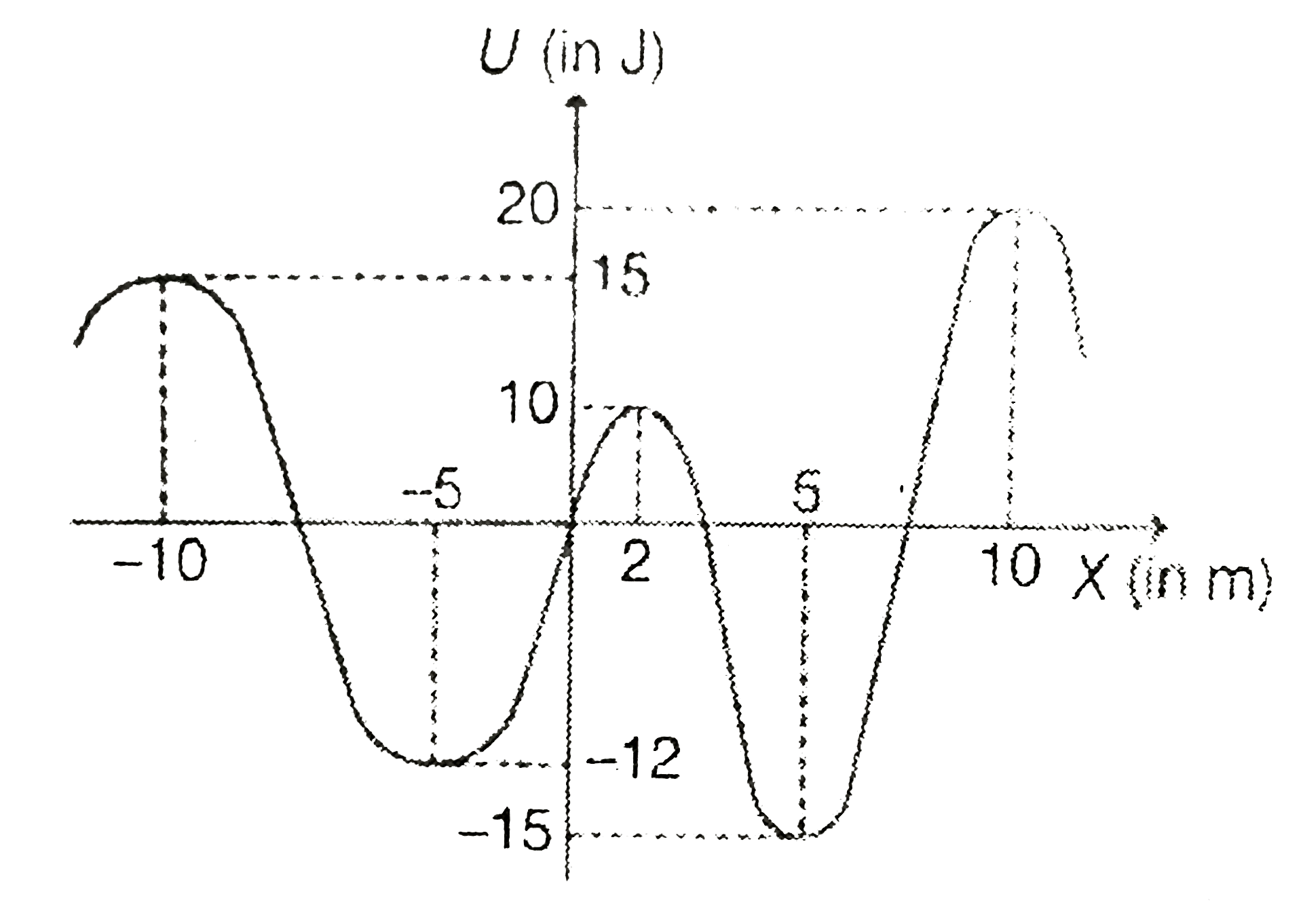
If the particle is released at the origin, then
View SolutionIn the figure the variation of potential energy of a particle of mass m=2kg is represented w.r.t. its x-coordinate. The particle moves under the effect of this conservative force along the x-axis.
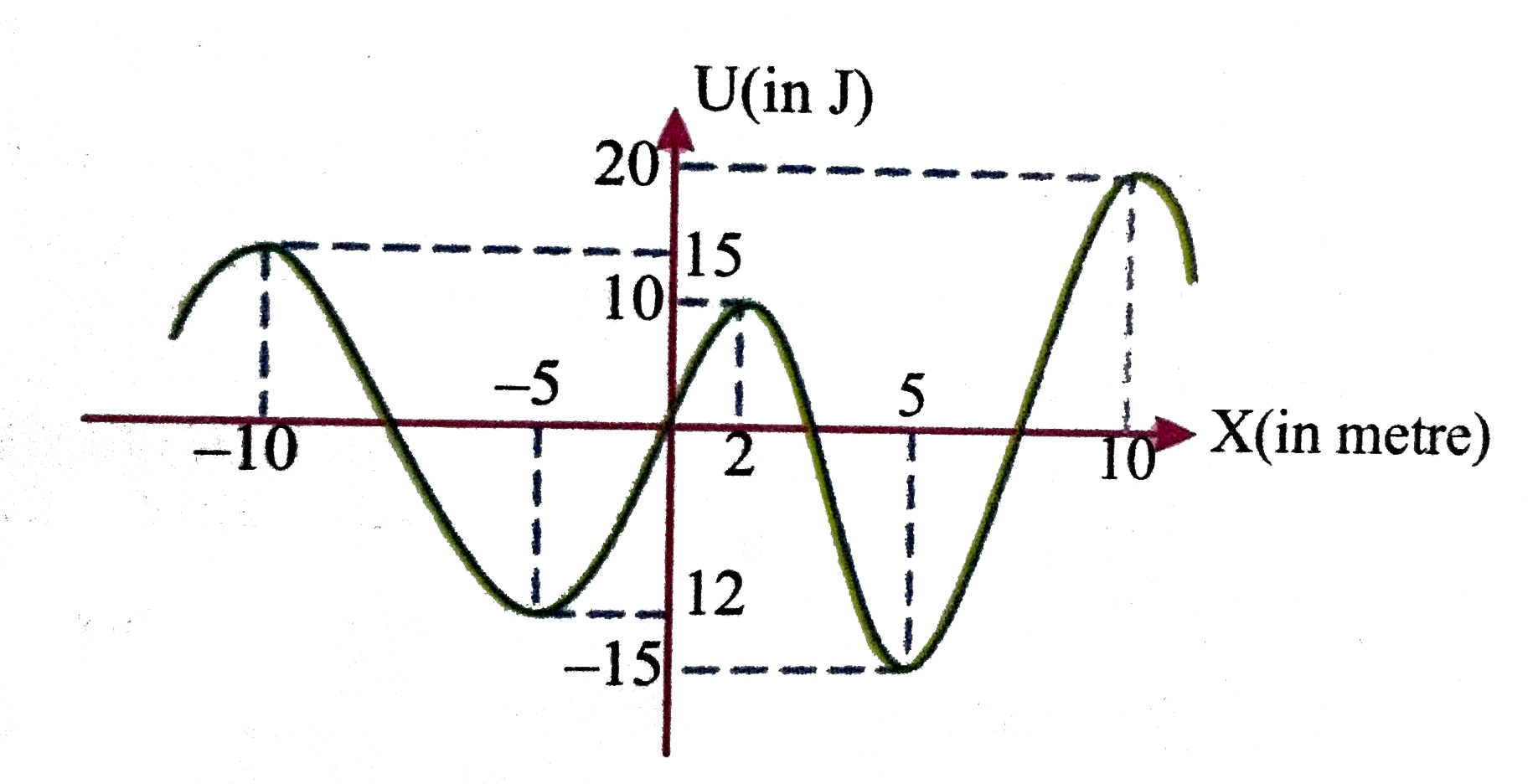
x=−5m and x=10m position of the particle are respectively of
View Solution
Knowledge Check
In figure, the variation of potential energy of a particle of mass m=2kg is represented w.r.t its x-coordinate. The particle moves under the effect of the conservative force along the x-axis. Which of the following statements is incorrect about the particle?
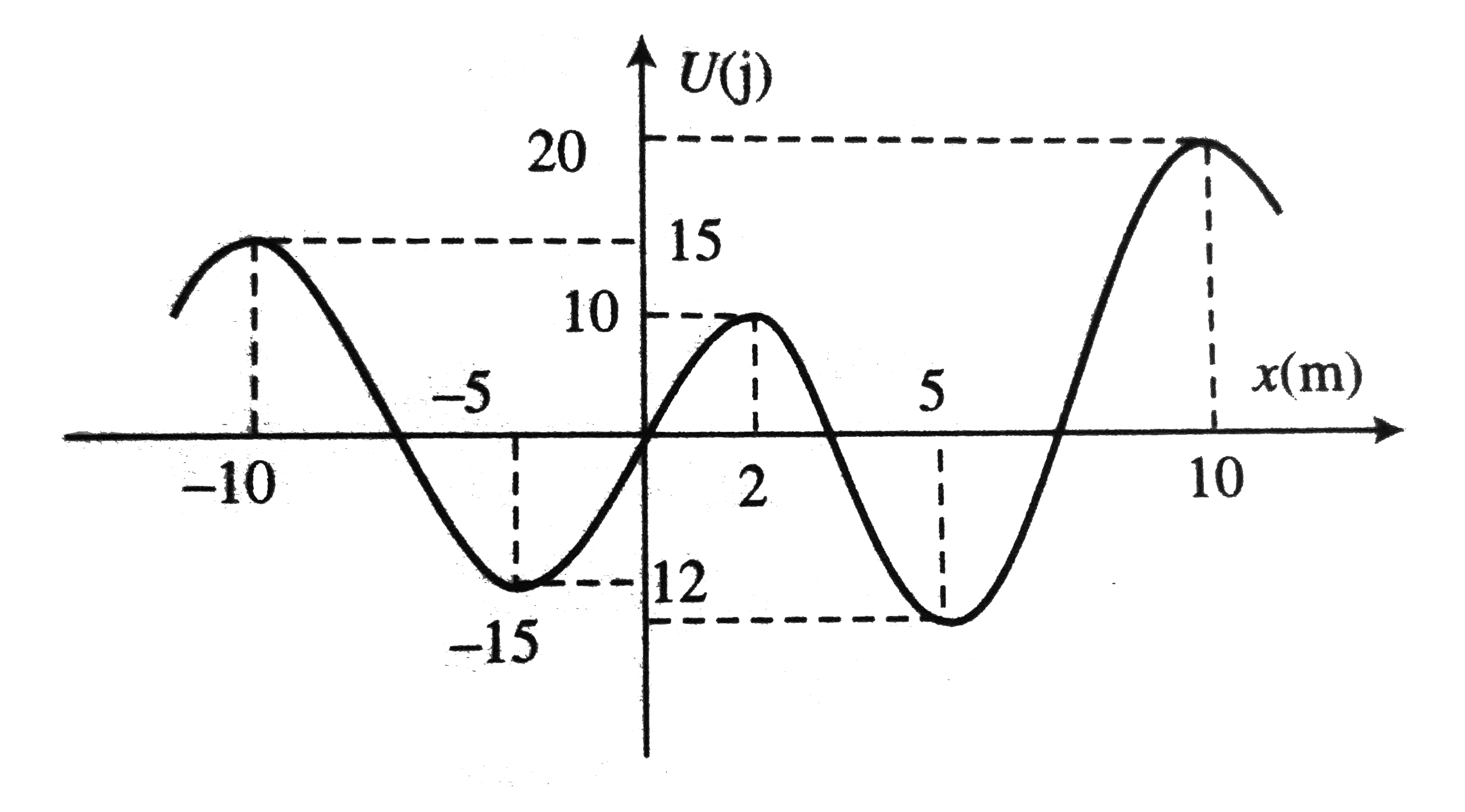 A(a) If it is released at the origin, it will move in negative x-axis.B(b) If it is released at x=2+Δ, where Δ→0, then its maximum speed will be 5ms−1 and it will perform oscillatory motion.C(c) If initially x=−10 and →u=√6ˆi, then it will cross x=10.D(d) x=−5 and x=+5 are unstable equilibrium positions of the particle.
A(a) If it is released at the origin, it will move in negative x-axis.B(b) If it is released at x=2+Δ, where Δ→0, then its maximum speed will be 5ms−1 and it will perform oscillatory motion.C(c) If initially x=−10 and →u=√6ˆi, then it will cross x=10.D(d) x=−5 and x=+5 are unstable equilibrium positions of the particle.In the figure the variation of potential energy of a particle of mass m=2kg is represented w.r.t. its x-coordinate. The particle moves under the effect of this conservative force along the x-axis.
If the particle is released at the origin thenAit will move towards positive x-axis.Bit will move towards negative x-axis.Cit will remain stationary at the origin.Dits subsequent motion cannot be decided due to lack of information.The variation of potential energy of a particle of mass m = 5kg to its x-coordinate . The particle moves under the effect of this conservative force only along the x-axis. Then, choose the correct option.
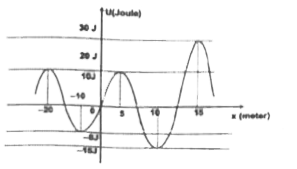 AIf the particle is released at the origin, then it will move towards x-axis.BAt x=10 particle is in unstable equilibriumCIf the particle is released at x=5+Δx, where Δx→0(Δx>0) then its maximum speed is √10m/sec.DAt x= 15m, the particle is in stable equilibrium.
AIf the particle is released at the origin, then it will move towards x-axis.BAt x=10 particle is in unstable equilibriumCIf the particle is released at x=5+Δx, where Δx→0(Δx>0) then its maximum speed is √10m/sec.DAt x= 15m, the particle is in stable equilibrium.
In the figure, the variation of potential energy of a particle of mass m = 2kg is represented with respect to its x-coordinate. The particle moves under the effect of this conservative force along the X-axis.
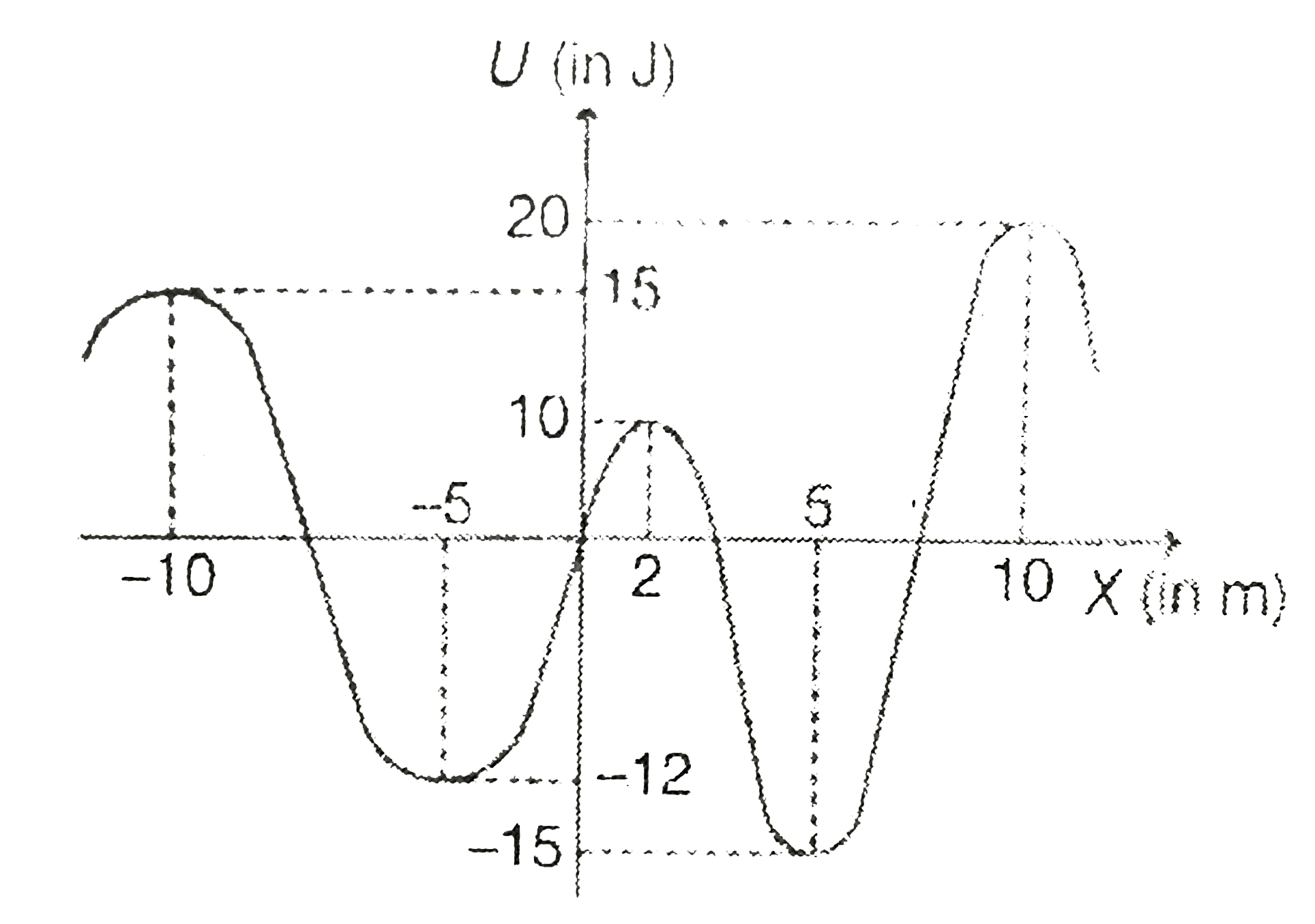
If the particle is released at x=2+Δ where Δ→0 (it is positive), then its maximum speed in subsequent motion will be
View SolutionFigure shows a plot of the potential energy as a function of x for a particle moving along the x-axis. Which of the following statement(s) is/are true?
View SolutionFor a particle moving along the x-axis, mark the correct statement(s).
View SolutionA particle moves along x-axis as x=4(t−2)+a(t−2)2
Which of the following is true?
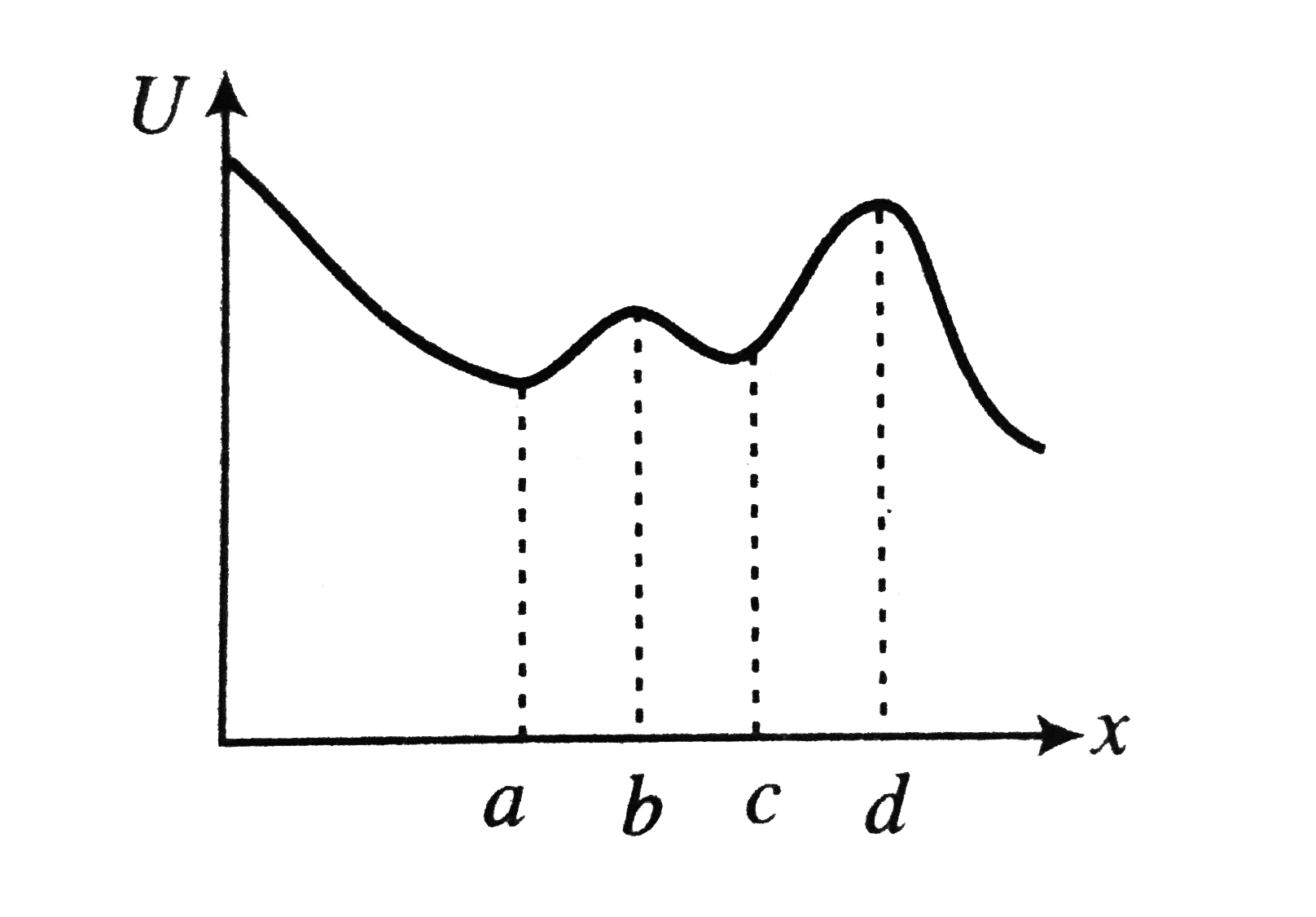
View SolutionIn the figure shown the potential energy U of a particle is plotted its position 'x' from origin. Then which of the following statement is correct A particle at :

View Solution
