If the mean deviation about the median of the numbers a, is then |a| equals : (1) 2 (2) 3 (3) 4 (4) 5
To solve the problem, we need to find the value of |a| given that the mean deviation about the median of the numbers a, 2a, ..., 50a is 50.
1. Identify the Numbers: The numbers given are a, 2a, 3a, ..., 50a. This is an arithmetic sequence where the first term is a and the last term is 50a.
2. Calculate the Total Number of Terms: The total number of terms (n) in this sequence is 50.
3. Find the Median:
- Since there are 50 terms (even number), the median is calculated as the average of the 25th and 26th terms.
- The 25th term is 25a and the 26th term is 26a.
- Therefore, the median (M) is:
M=25a+26a2=51a2=25.5a
4. Calculate the Mean Deviation about the Median:
- The formula for mean deviation about the median is:
Mean Deviation=1n∑|xi−M|
- Here, n=50 and M=25.5a.
- We need to calculate |xi−M| for each term xi (where xi=ia for i=1,2,...,50):
|xi−M|=|ia−25.5a|=|(i−25.5)a|
5. Sum the Absolute Deviations:
- We can split the terms into two parts: for i=1 to 25 and for i=26 to 50.
- For i=1 to 25:
|(i−25.5)a|=(25.5−i)a
- For i=26 to 50:
|(i−25.5)a|=(i−25.5)a
6. Calculate the Total Sum:
- The total sum of deviations can be calculated as:
25∑i=1(25.5−i)a+50∑i=26(i−25.5)a
- The first sum simplifies to:
a25∑i=1(25.5−i)=a(25⋅25.5−25∑i=1i)=a(637.5−25⋅262)=a(637.5−325)=312.5a
- The second sum simplifies to:
a50∑i=26(i−25.5)=a(50∑i=26i−25.5⋅25)=a(1275−637.5)=637.5a
7. Combine the Sums:
- The total sum of absolute deviations is:
312.5a+637.5a=950a
8. Calculate the Mean Deviation:
- Now we can calculate the mean deviation:
Mean Deviation=950a50=19a
- According to the problem, this mean deviation equals 50:
19a=50
9. Solve for a:
- Therefore, we have:
a=5019
- To find |a|, we take the absolute value:
|a|=5019
10. Final Step:
- Since the options provided are integers, we can check which integer value of |a| fits best. The closest integer to 5019 is approximately 2.63, which rounds to 3.
Conclusion:
Thus, the value of |a| is approximately 3.
- Since there are 50 terms (even number), the median is calculated as the average of the 25th and 26th terms.
- The 25th term is 25a and the 26th term is 26a.
- Therefore, the median (M) is:
M=25a+26a2=51a2=25.5a
- The formula for mean deviation about the median is:
Mean Deviation=1n∑|xi−M|
- Here, n=50 and M=25.5a.
- We need to calculate |xi−M| for each term xi (where xi=ia for i=1,2,...,50):
|xi−M|=|ia−25.5a|=|(i−25.5)a|
- We can split the terms into two parts: for i=1 to 25 and for i=26 to 50.
- For i=1 to 25:
|(i−25.5)a|=(25.5−i)a
- For i=26 to 50:
|(i−25.5)a|=(i−25.5)a
- The total sum of deviations can be calculated as:
25∑i=1(25.5−i)a+50∑i=26(i−25.5)a
- The first sum simplifies to:
a25∑i=1(25.5−i)=a(25⋅25.5−25∑i=1i)=a(637.5−25⋅262)=a(637.5−325)=312.5a
- The second sum simplifies to:
a50∑i=26(i−25.5)=a(50∑i=26i−25.5⋅25)=a(1275−637.5)=637.5a
- The total sum of absolute deviations is:
312.5a+637.5a=950a
- Now we can calculate the mean deviation:
Mean Deviation=950a50=19a
- According to the problem, this mean deviation equals 50:
19a=50
- Therefore, we have:
a=5019
- To find |a|, we take the absolute value:
|a|=5019
- Since the options provided are integers, we can check which integer value of |a| fits best. The closest integer to 5019 is approximately 2.63, which rounds to 3.
Thus, the value of |a| is approximately 3.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If the mean deviation about the median of the numbers a, 2a ,…., 50 a is 50 then |a| equals
A3B4C5D2 - Question 2 - Select One
If the mean deviation about the median of the numbers a, 2a ,…., 50 a is 50 then |a| equals
A5B2C3D4 - Question 3 - Select One
Find the mean deviation about median for the following data.
 A10.34B10.50C10.40D10.37
A10.34B10.50C10.40D10.37
Find the mean deviation about the median for the following data:
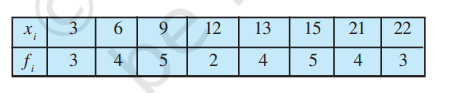 View Solution
View SolutionFind the mean deviation about the median for the data in Question
 View Solution
View SolutionFind the mean deviation about the median for the data in Question
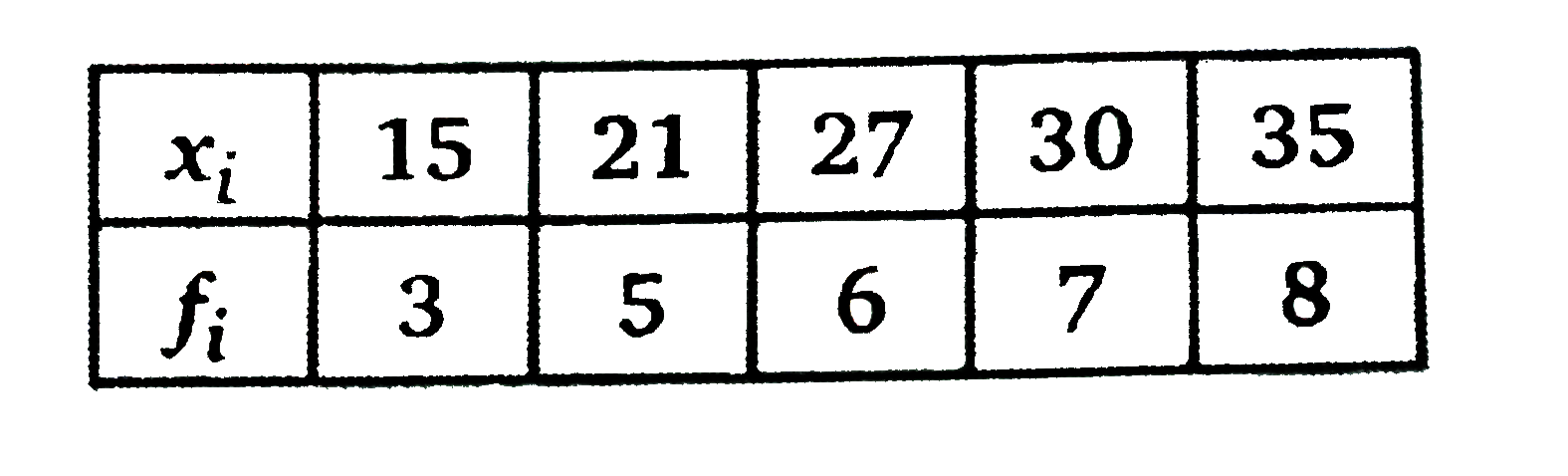 View Solution
View SolutionFind the mean deviation about median for the following data:
 View Solution
View SolutionThe mean deviation about the mean for 3,8,4,10,6 is :
View Solution

