sinθ=cos□
To solve the equation sinθ=cos2θ, we can follow these steps:
Step 1: Use the Pythagorean Identity
We know that cos2θ+sin2θ=1. From this identity, we can express cos2θ in terms of sinθ:
cos2θ=1−sin2θ
Step 2: Substitute into the Equation
Now, we can substitute cos2θ in the original equation:
sinθ=1−sin2θ
Step 3: Rearrange the Equation
Rearranging the equation gives us:
sin2θ+sinθ−1=0
Step 4: Use the Quadratic Formula
This is a quadratic equation in terms of sinθ. We can use the quadratic formula x=−b±√b2−4ac2a where a=1,b=1,c=−1:
sinθ=−1±√12−4⋅1⋅(−1)2⋅1
=−1±√1+42
=−1±√52
Step 5: Find Possible Values of sinθ
Thus, we have two possible values for sinθ:
sinθ=−1+√52andsinθ=−1−√52
Step 6: Evaluate the Validity of the Values
Since sinθ must be in the range of (−1,1), we need to check the values:
- For sinθ=−1+√52:
- Approximate value: −1+2.2362≈0.618 (valid)
- For sinθ=−1−√52:
- Approximate value: −1−2.2362≈−1.618 (invalid)
Conclusion
The only valid solution is:
sinθ=−1+√52
We know that cos2θ+sin2θ=1. From this identity, we can express cos2θ in terms of sinθ:
cos2θ=1−sin2θ
Now, we can substitute cos2θ in the original equation:
sinθ=1−sin2θ
Rearranging the equation gives us:
sin2θ+sinθ−1=0
This is a quadratic equation in terms of sinθ. We can use the quadratic formula x=−b±√b2−4ac2a where a=1,b=1,c=−1:
sinθ=−1±√12−4⋅1⋅(−1)2⋅1
=−1±√1+42
=−1±√52
Thus, we have two possible values for sinθ:
sinθ=−1+√52andsinθ=−1−√52
Since sinθ must be in the range of (−1,1), we need to check the values:
- For sinθ=−1+√52:
- Approximate value: −1+2.2362≈0.618 (valid)
- For sinθ=−1−√52:
- Approximate value: −1−2.2362≈−1.618 (invalid)
The only valid solution is:
sinθ=−1+√52
Topper's Solved these Questions
- COVERAGE STANDARD QUESTION BOOK - UNIQUE PUBLICATIONCHAPTER - COVERAGE STANDARD QUESTION EXERCISE - 2 Mark Questions
73 Videos
- CO-ORDINATE GEOMETRYBOOK - UNIQUE PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Assignment-V
8 Videos
- FINANCIAL PLANNINGBOOK - UNIQUE PUBLICATIONCHAPTER - FINANCIAL PLANNINGEXERCISE - UNIQUE PRACTICE SESSION (4 MARK QUESTION )
1 Videos
Similar Questions
Knowledge Check
cosθ[cosθsinθ−sinθcosθ]+sinθ[sinθ−cosθcosθsinθ] is equal to
A[1001]B[0110]C[0011]DNone of theseIf sinθ+cosθsinθ−cosθ=3, then the value of sin4θ−cos4θ is:
A2nπB2nπ+π2C2nπ−π2Dnπ
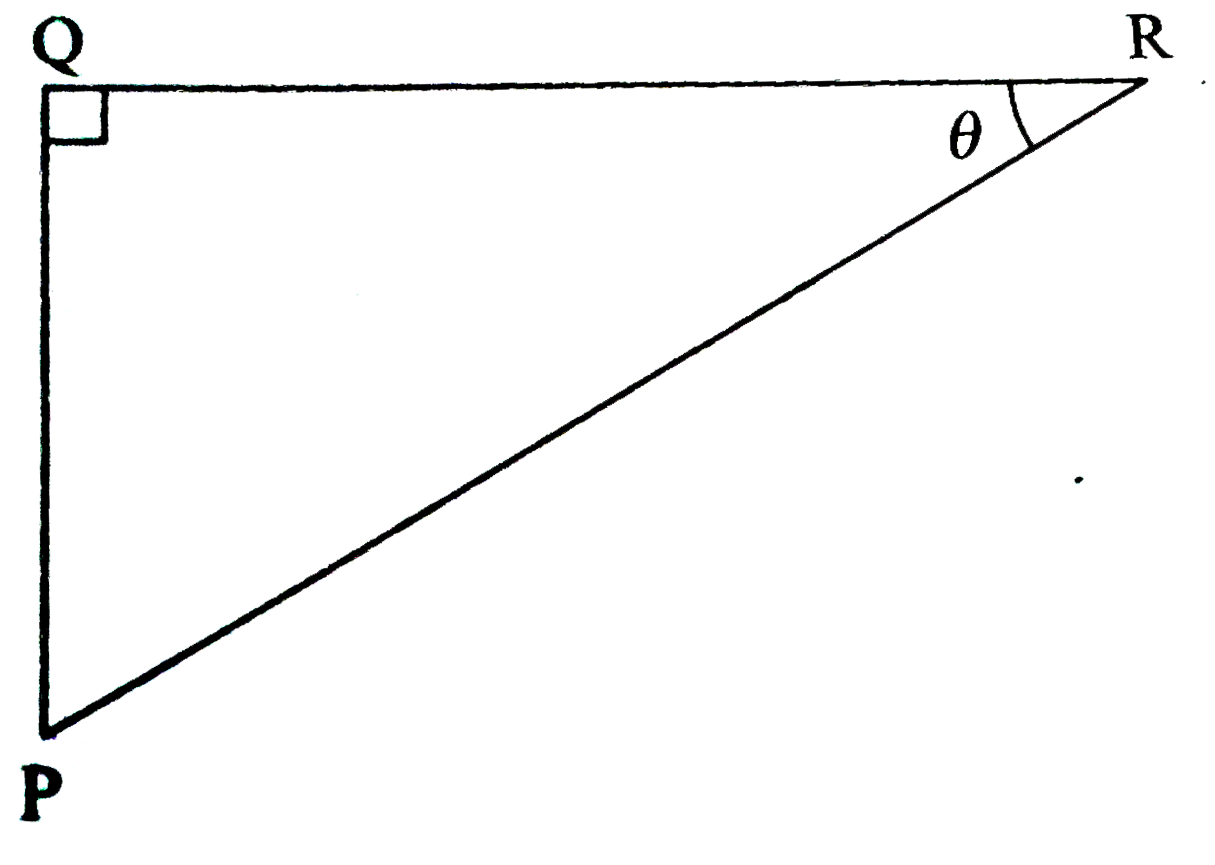
In the figure sinθ=□,tanθ=□
View SolutionProve cotθ+tanθ=(cosecθ)(secθ) by completing the following activity: LHS=cotθ+tanθ =cosθsinθ+□cosθ =□+□sinθ×cocosθ =□sinθ×cosθ =1□×1□ =cosecθ×secθ =RHS ∴cotθ+tanθ=cosecθ×secθ
View SolutionSimplify: cosθ[cosθsinθ−sinθcosθ]+sinθ[sinθ−cosθcosθsinθ]
View Solution((cosθ+sinθ)4−(cosθ−sinθ)4sinθcosθ)=?
View SolutionIf cosθ+sinθ=√2cosθ, then the value of cosθ−sinθsinθ is
View Solution(sinθ+cosθ)(1−sinθcosθ)=sin3θ+cos3θ
View Solution
