Show that the equation
represents.
An ellipse if 'c' is a real constant less than 5.Solution in Telugu
Step by step video & image solution for Show that the equation (x^(2))/(9-c)+(y^(2))/(5-c)=1 represents. An ellipse if 'c' is a real constant less than 5. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- HYPERBOLABOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - HYPERBOLAEXERCISE - VSAQ
1 Videos
- HYPERBOLABOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - HYPERBOLAEXERCISE - SAQ
2 Videos
- HYPERBOLABOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - HYPERBOLAEXERCISE - SAQ
2 Videos
- ELLIPSEBOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - ELLIPSEEXERCISE - EXERCISE 4(B)
15 Videos
- INTEGRATIONBOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - INTEGRATIONEXERCISE - DAM SURE LAQ - 8 MARKS
9 Videos
Similar Questions
Find the equation of the hyperbola whose foci are (±5,0) the transverse axis is of length 8.
View SolutionFind the equation of the tangents to the hyperbola 3x2−4y2=12 which are (i) Parallel and (ii) perpendicular to the line y=x−7
View SolutionFind the equation of the tangents to the hyperbola 3x2−4y2=12 which are (i) Parallel and (ii) perpendicular to the line y=x−7
View SolutionFind the equation of tangent and normal to the ellipse x2+8y2=33 at (-1,2).
View SolutionEvaluate the integerals.
∫2cosx+3sinx4cosx+5sinxdx
View SolutionThe SN1 reactivity of the following halides will be in the order:
(i) (CH3)3C−Br
(ii) (C6H5)CHBr
(iii) (C6H5)2C(CH3)Br
(iv) (CH3)2CHBr
(v) C2H5Br
View SolutionThe name of
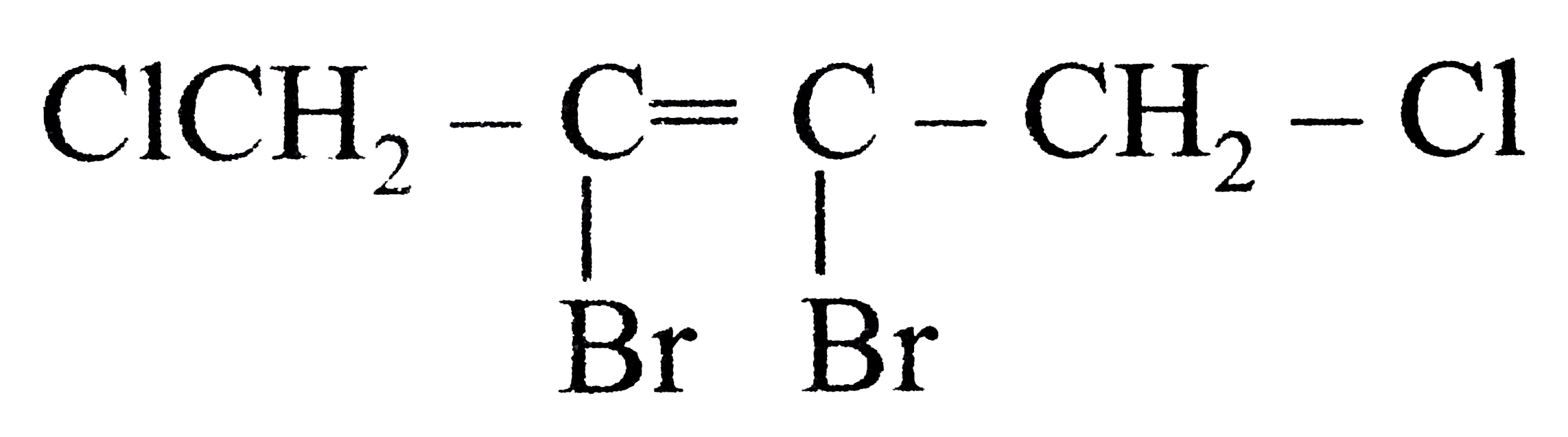according to IUPAC nomenclature system is :
View SolutionThe complex [Cr(H2O)5Cl]Brand[Cr(H2O)5Br]Cl show
View SolutionShow that the equation
x29−c+y25−c=1 represents.
A hyperbola if c is any real constant between 5 and 9.
View SolutionThe equation of the ellipse is (x−1)2+(y−1)2=19(3x+4y−55)2, then the length of minor axis of this ellipse is
View SolutionIf y=x+c is a normal to the ellipse x225+y29=1, then c2=
View Solution(i) Show that the equation x29−c+y25−c=1 represents (a) an ellipse if c is a real constant less than 5 (b) a hyperbola if c is any real constant between 5 and 9.
(ii) Show that each ellipse in (a) and each hyperbola in (b) has foci at the two points (±2,0) independent of the value of c.
View SolutionIf the equation x29−k+y25−k=1 represents an ellipse then
View SolutionIf y = x + c is a normal to the ellipse x29+y24=1 , then c2 is equal to
View Solution(i) Show that equation x29−c+y25−c=1 represents
(a) an ellipse if c is a real constant less than 5
(b) a hyperbola if c is any real constant between 5 and 9
(ii) Show that each ellipse in
(a) and each hyperbola in
(b) has foci at the two points (±2,0), independent of the value of c.
View Solution