Consider : Statement I : (pˆ˜q)ˆ~pˆq is a fallacy. Statement II : (p→q)↔(~q→˜p) is a tautology. (1) Statement - I is True; Statement -II is true; Statement-II is not a correct explanation for Statement-I (2) Statement -I is True; Statement -II is False. (3) Statement -I is False; Statement -II is True (4) Statement -I is True; Statement -II is True; Statement-II is a correct explanation for Statement-I
Step by step video & image solution for Consider : Statement I : (phat~""q)hat(~""phatq) is a fallacy. Statement II : (pvecq)harr(~""qvec~""p) is a tautology. (1) Statement - I is True; Statement -II is true; Statement-II is not a correct explanation for Statement-I (2) Statement -I is True; Statement -II is False. (3) Statement -I is False; Statement -II is True (4) Statement -I is True; Statement -II is True; Statement-II is a correct explanation for Statement-I by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Statement - I : The value of the integral ∫π/3π/6dx1+√tanx is equal to π6 . Statement - II : ∫baf(x)dx=∫baf(a+b−x)dx. (1) Statement - I is True; Statement -II is true; Statement-II is not a correct explanation for Statement-I (2) Statement -I is True; Statement -II is False. (3) Statement -I is False; Statement -II is True (4) Statement -I is True; Statement -II is True; Statement-II is a correct explanation for Statement-I
View SolutionGiven : A circle, 2x2+2y2=5 and a parabola, y2=4√5x . Statement - I : An equation of a common tangent to these curves is y=x+√5 Statement - II : If the line, y=mx+√5m(m≠0) is their common tangent, then m satisfies m4−3m2+2=0. (1) Statement - I is True; Statement -II is true; Statement-II is not a correct explanation for Statement-I (2) Statement -I is True; Statement -II is False. (3) Statement -I is False; Statement -II is True (4) Statement -I is True; Statement -II is True; Statement-II is a correct explanation for Statement-I
View Solution
Knowledge Check
Consider following statements Statement - I :
(p^~a)^(vpng) is a fallacy.
Statement - II : (p→q)↔(~q→~p) is a tautology.AStatement - I is true, statement -II is false.BStatement - I is false, Statement - II is true.CStatement - I true, Statement - II is true, Statement - II is a correct explanation for Statement - I.DStatement - I is true, Statement - II is true, Statement - II is not a correct explanation for Statement - I.Consider :
Statement I:
(p∧~q)∧(~p∧q) is a fallacy
Statement II: (p→q)↔(~q→~p) is a tautologyAStatement-1 is true, statement 2 is true, statement 2 is a correct explanation for statement 1BStatement 1 is true, statement-2 is true, statement 2 is not a correct explanation for statement 1CStatement 1 is true , statement 2 is false,Dstatement 1 is false, statement 2 is true
Let A be a 2×2 matrix with non-zero entries and let A2=I , where I is 2×2 identity matrix. Define Tr(A) = sum of diagonal elements of A and |A| = determinant of matrix A. Statement-1: Tr(A)=0 Statement-2: |A|=1 (1) Statement-1 is true, Statement-2 is true; Statement-2 is not the correct explanation for Statement-1 (2) Statement-1 is true, Statement-2 is false (3) Statement-1 is false, Statement-2 is true (4) Statement-1 is true, Statement-2 is true; Statement-2 is the correct explanation for Statement-1
View SolutionLet f: R R be a continuous function defined by f(x)=1ex+2e−x . Statement-1: f(c)=13, for some c∈R . Statement-2: 0<f(x)≤12√2, for all x∈R . (1) Statement-1 is true, Statement-2 is true; Statement-2 is not the correct explanation for Statement-1 (2) Statement-1 is true, Statement-2 is false (3) Statement-1 is false, Statement-2 is true (4) Statement-1 is true, Statement-2 is true; Statement-2 is the correct explanation for Statement-1
View SolutionStatement-1: The point A(3, 1, 6) is the mirror image of the point B(1, 3, 4) in the plane xy+z=5 . Statement-2: The plane x xy+z=5 bisects the line segment joining A(3, 1, 6) and B(1, 3, 4). (1) Statement-1 is true, Statement-2 is true; Statement-2 is not the correct explanation for Statement-1 (2) Statement-1 is true, Statement-2 is false (3) Statement-1 is false, Statement-2 is true (4) Statement-1 is true, Statement-2 is true; Statement-2 is the correct explanation for Statement-1
View SolutionEach question has 5 choices (a) ,(b) ,(c ) (d) and (e ) out of which ONLY ONE is correct.
(a) Statement -1 is True, Statement -2 is True , Statement -2 is a correct explanation for Statement -1.
(b) Statement -1 is True, Statement -2 is True, Statement -2 is NOT a correct explanation for Statement -1.
(C ) Statement -1 is True, Statement -2 is False.
(d) Statement -1 is False, Statement -2 is True.
(e) Statement -1 and Statement -2 both are False.
Statement -1: Effective molecular mass of acetic acid is 120.
Statement -2: It forms dimer due to intramolecular H-bonding.
View SolutionIf A is 2 x 2 invertible matrix such that A=adjA−A−1 Statement-I 2A2+I=O(null matrix) Statement-II: 2|A|=1 (i) Statement-I is true, Statement-II is true; Statement-II is a correct explanation for Statement-I (2) Statement-I is true, Statement-II is true; Statement-II is not a correct explanation for Statement-I. 3) Statement-I is true, Statement-II is false. (4) Statement-I is false, Statement-II is true.
View SolutionEach question has 5 choices (a) ,(b) ,(c ) (d) and (e ) out of which ONLY ONE is correct.
(a) Statement -1 is True, Statement -2 is True , Statement -2 is a correct explanation for Statement -1.
(b) Statement -1 is True, Statement -2 is True, Statement -2 is NOT a correct explanation for Statement -1.
(C ) Statement -1 is True, Statement -2 is False.
(d) Statement -1 is False, Statement -2 is True.
(e) Statement -1 and Statement -2 both are False.
Statement -1: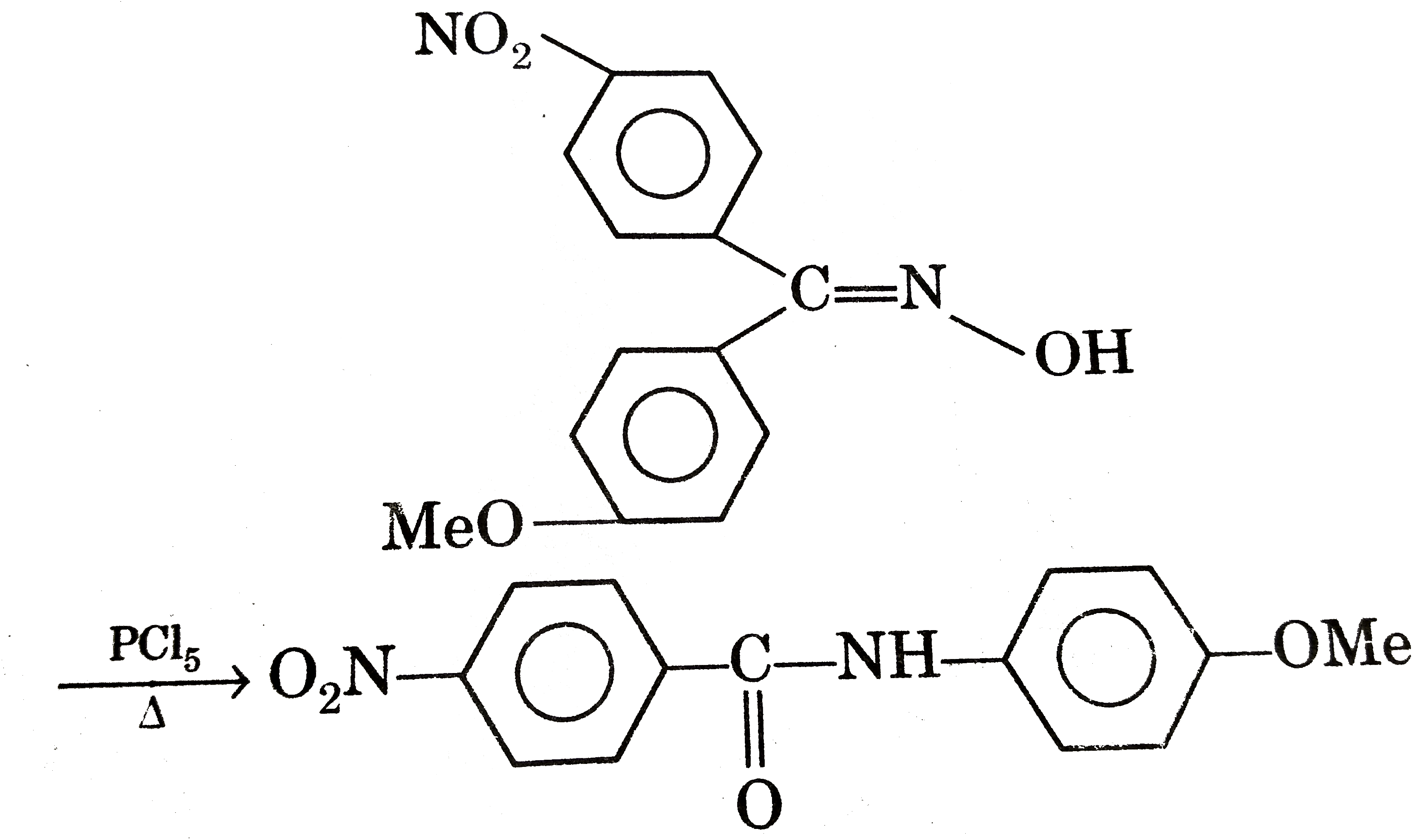
Statement -2: Migratory aptitude of p-methoxyphenyl group is greater than migratory aptitude p-nitrophenyl of group during carbrocation rearrangements.
View Solution
