A point P is 3units away from line L1=3x+4y+5=0and4 units away from the line L2=8x−by+9=0, The reflection of P on L1, is P1 the reflection of P1 on L2, is P2 the reflection of P3, on L2, is P4, Then the area (in sq. units) of figure formed by joining P1P2P3,andP4, is-
Step by step video & image solution for A point P is 3units away from line L_1= 3x + 4y +5=0 and 4 units away from the line L_2 = 8x-by +9=0, The reflection of P on L_1, is P_1 the reflection of P_1 on L_2, is P_2 the reflection of P_3, on L_2, is P_4, Then the area (in sq. units) of figure formed by joining P_1P_2P_3, and P_4, is- by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
The reflection of point P(2,−1) in line y=3x−1 is Q and reflection of P in line y=9−2x is R. thencircumcentre of APQR is (a,b), where (a+b) is equal to
View SolutionPoints (4,0) and (-3,0) are invarient points under reflection in line L1, point (0,5) and (0,-2) are invarient under reflection in line L2.
Write P' . The reflection of P(6,−8) in L1andP'' the image of P in L2.
View Solution
Knowledge Check
The image of the point A (1,0,0) in the line x−12=x+1−3=z+108 is :
A(3,−4,−2)B(1,−1,10)C(5,−8,−4)D(2,−1,8)P1:x+3y−z=0andP2:y+2z=0 are two intersecting planes P3 is a plane passing through the point (2,1,-1) and through the line of intersection of P1andP2
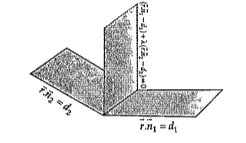
Distance of P3 from origin is _______ units.A0B1C1√5D1110
A point P is its own image under the reflection in a line l. Describe the position of the point P with respect to the line l.
View SolutionLet L1:x−13=y−21=z−3−3 be a line and P : 4x + 3y + 5z = 50 be a plane. L2 is parallel to the line L1. If a plane P containing both the lines L1 and L2 are given by the equation
14x - by+ 5z + d = 0 (b,d ∈ R), then the value of (b-d) is equal to
View SolutionPoint (-5,0) and (4,0) are invariant point under reflection in the line L1, point (0,-6) and (0,5) are invariant on reflection in the line L2 .
Write down the image of P and Q on reflection in L2 . Name the images as P'' and Q'' respectively.
View SolutionThe points P (4, 1) and Q (-2, 4) are reflected in line y = 3. Find the co-ordinates of P', the image of P and Q', the image of Q.
View SolutionPoints (3, 0) and (-1,0) are invariant points under reflection in the line L1 points (0, -3) and (0, 1) are invariant points on reflection in line L2
Write down the images of P (3,4) and Q (-5,-2) on reflection in L2 Name the images as P" and Q" respectively.
View SolutionPoint (-5,0) and (4,0) are invariant point under reflection in the line L1, point (0,-6) and (0,5) are invariant on reflection in the line L2 .
Write down the image of P(2,6) and Q (-8,-3) on reflection in L1 . Name the images as P' and Q' respectively.
View Solution
