A body is dropped from a certain height.
the time taken to travel first half of the height is greater than that for second half.
time time taken to travel first half of the height is less than that for second half
the time taken to travel first half of the height is equal to that for second half
any one of the above three situations may be correct depending upon the value of height.
The correct Answer is:A
To solve the problem of a body dropped from a certain height and to determine the time taken to travel the first half of the height compared to the second half, we can follow these steps:
1. Understanding the Problem:
- A body is dropped from a height h. We need to analyze the time taken to cover the first half of the height (h/2) and the second half of the height (h/2).
2. Using Kinematic Equations:
- The kinematic equation for an object under free fall (with initial velocity u=0) is given by:
s=ut+12at2
- Here, s is the distance traveled, a is the acceleration due to gravity (g), and t is the time taken.
3. Calculating Time for the First Half:
- For the first half of the height (h/2):
h2=0⋅t1+12gt21
Simplifying this gives:
h=gt21⟹t1=√hg
4. Calculating Time for the Second Half:
- For the second half of the height, the body has already fallen h/2 and has a velocity v when it reaches this point. We need to find the time t2 to fall the second half.
- The velocity at the end of the first half can be calculated using:
v=u+at=0+gt1=g√hg=√gh
- Now, using the kinematic equation for the second half:
h2=vt2+12gt22
Substituting v=√gh:
h2=√ght2+12gt22
5. Comparing Times:
- From the analysis, we can see that the body accelerates as it falls. Thus, it takes more time to cover the first half of the height than the second half because the velocity increases as the body falls.
- Therefore, we conclude that:
t1>t2
6. Final Conclusion:
- The time taken to travel the first half of the height is greater than that of the second half. Thus, the correct option is:
t1>t2
- A body is dropped from a height h. We need to analyze the time taken to cover the first half of the height (h/2) and the second half of the height (h/2).
- The kinematic equation for an object under free fall (with initial velocity u=0) is given by:
s=ut+12at2
- Here, s is the distance traveled, a is the acceleration due to gravity (g), and t is the time taken.
- For the first half of the height (h/2):
h2=0⋅t1+12gt21
Simplifying this gives:
h=gt21⟹t1=√hg
- For the second half of the height, the body has already fallen h/2 and has a velocity v when it reaches this point. We need to find the time t2 to fall the second half.
- The velocity at the end of the first half can be calculated using:
v=u+at=0+gt1=g√hg=√gh
- Now, using the kinematic equation for the second half:
h2=vt2+12gt22
Substituting v=√gh:
h2=√ght2+12gt22
- From the analysis, we can see that the body accelerates as it falls. Thus, it takes more time to cover the first half of the height than the second half because the velocity increases as the body falls.
- Therefore, we conclude that:
t1>t2
- The time taken to travel the first half of the height is greater than that of the second half. Thus, the correct option is:
t1>t2
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONEXERCISE - Relative Motion In One Dimension20videos
GENERAL KINEMATICS AND MOTION IN ONE DIMENSION
- BOOK - A2ZCHAPTER - GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONEXERCISE - Understanding Motion Through Graphs40videos
GENERAL KINEMATICS AND MOTION IN ONE DIMENSION
- BOOK - A2ZCHAPTER - GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONEXERCISE - Motion With Constant Acceleration30videos
GENERAL KINEMATICS AND MOTION IN ONE DIMENSION
- BOOK - A2ZCHAPTER - FLUID MECHANICSEXERCISE - Chapter Test29videos
FLUID MECHANICS
- BOOK - A2ZCHAPTER - GRAVITATIONEXERCISE - Chapter Test29videos
GRAVITATION
Similar Questions
Knowledge Check
- Question 1 - Select One
A ball is dropped from a certain height to fall under gravity. After 1 sec another ball is dropped from the same point. What is the distance between them after 3 s from the dropping of second ball?
A35 mB25 mC50 mDnone - Question 2 - Select One
A ball is dropped from a certain height on a horizontal floor. The coefficient of restitution between the ball and the floor is 12. The displacement time graph of the ball will be.
A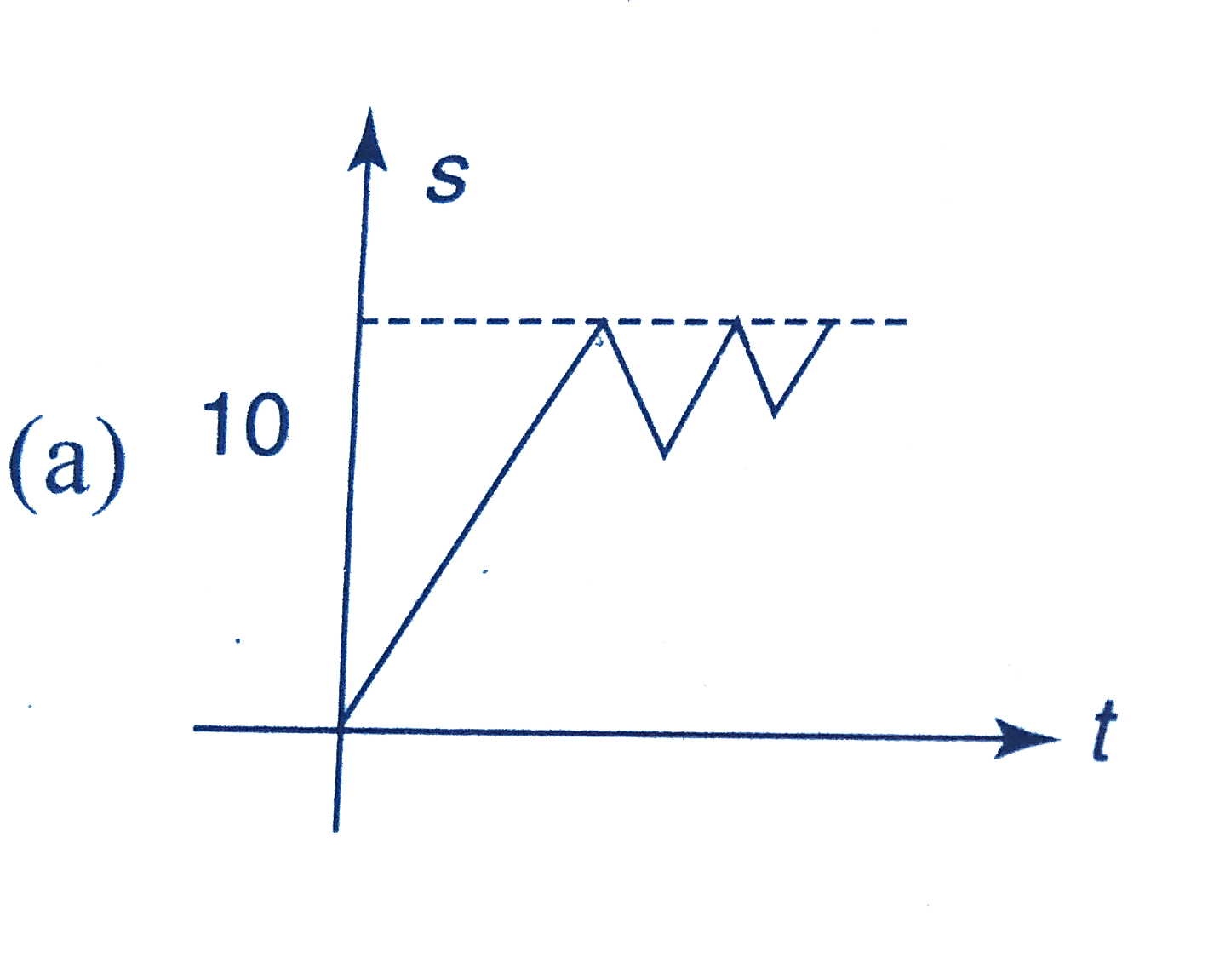 .B
.B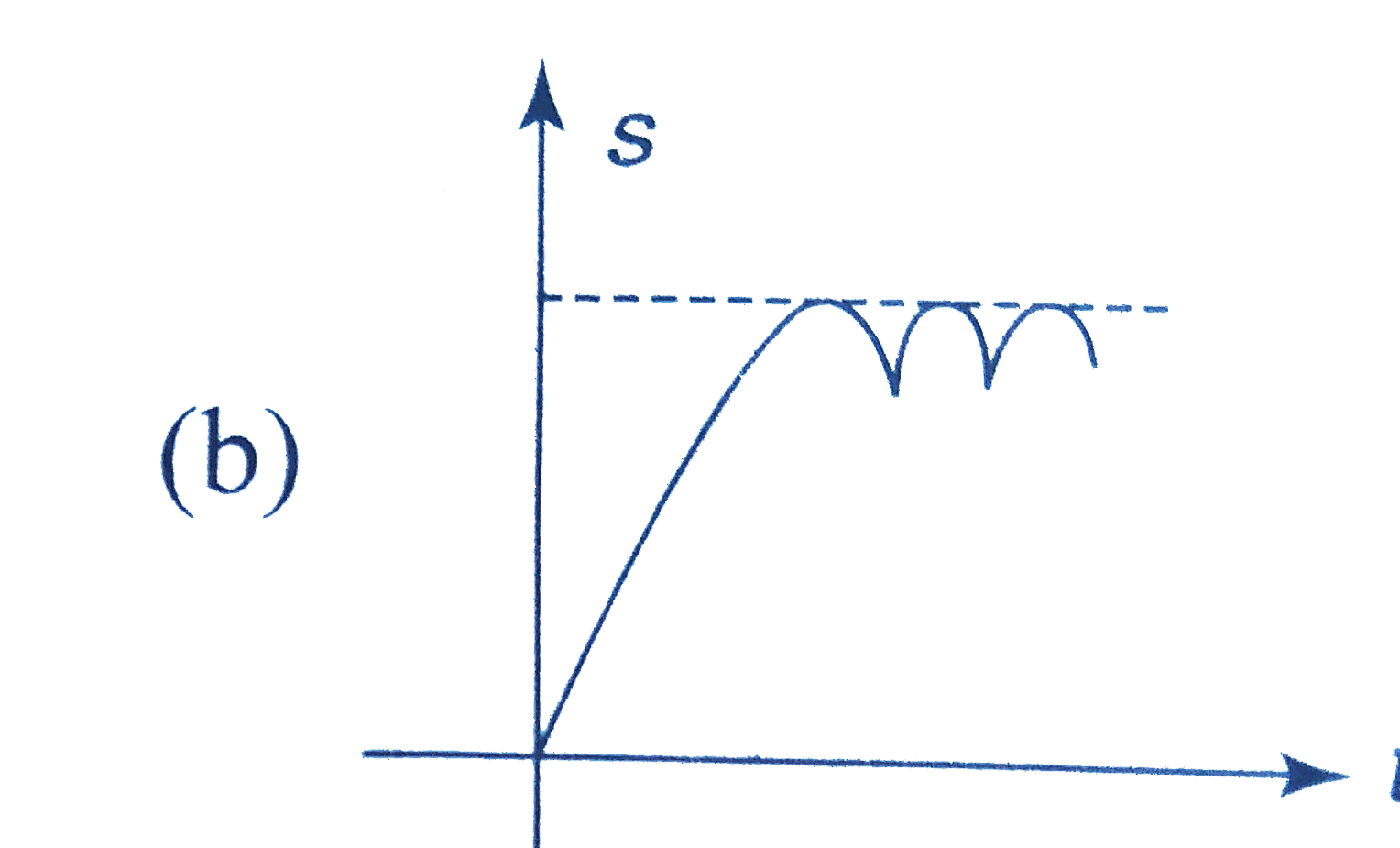 .C
.C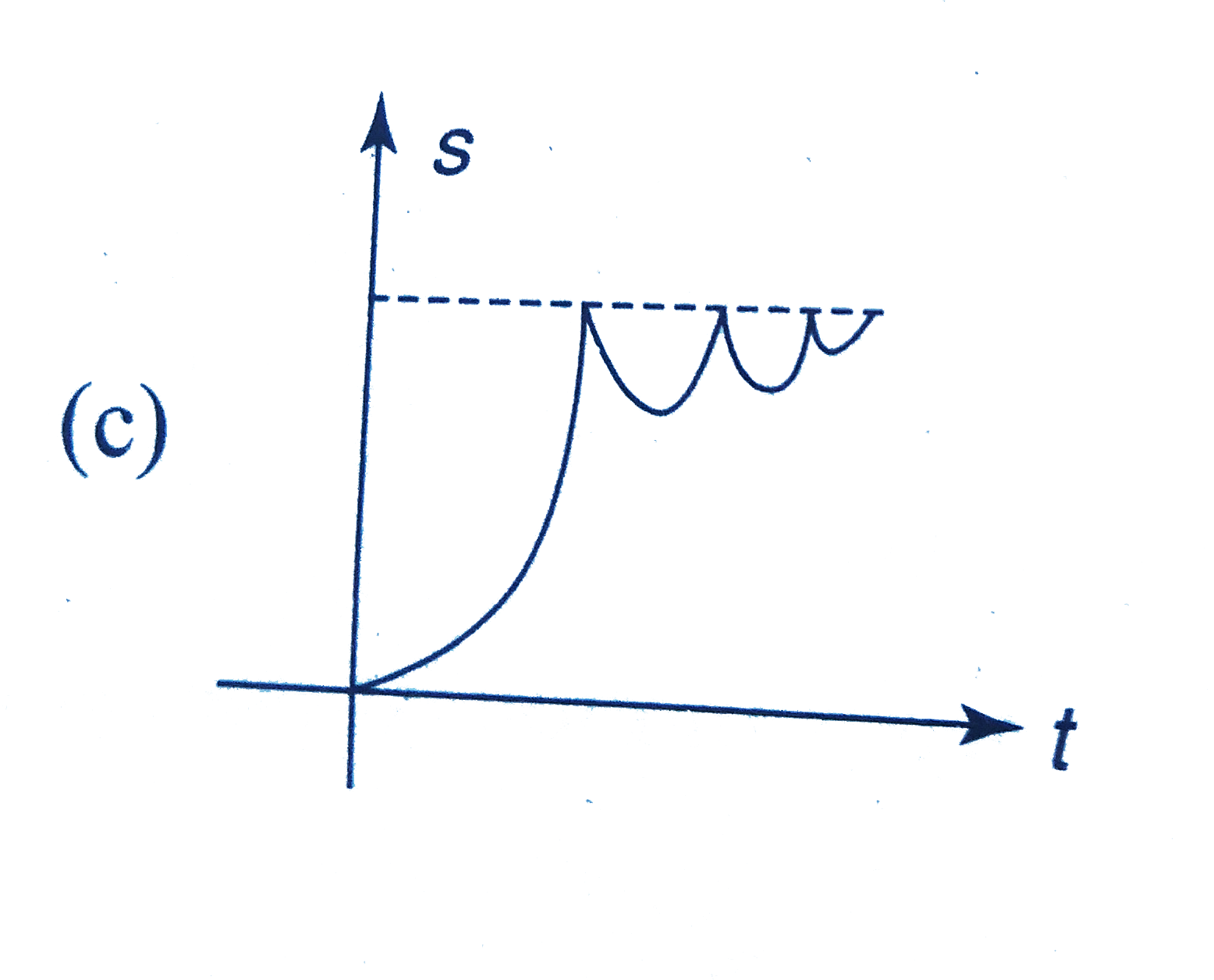 .D
.D .
. - Question 3 - Select One
A body dropped form a certain height strikes the ground and rises to a height of 108 cm , after striking the ground . The Coeffiednt of restitution is 0.6 . What is the height form which the body was dropped ?
A2 mB3 mC3.5 mD4 m
When a ball is dropped from a certain height the speed of the ball goes on increasing due to
View SolutionA small ball is dropped from a certain height on the surface of a non-viscous liquid of density less than the density of ball. The motion of the ball is
View SolutionA ball is dropped from certain height on a glass floor so that it rebounds elastically to the same height. If the process continues, the velocity -time graph for such a motion would be -
 View Solution
View SolutionA ball is dropped from the certain height on the surface of glass. It is collide elastically the comes back to initial position. If this process it repeated then velocity time graph is:-
View SolutionA body of mass m dropped from a certain height strikes a light vertical fixed spring of stifness k. the height of its fall before touching the spring the if the maximum compression of the spring the equal to 3mgk is
View Solution

