Refer Q.95. If the man takes t1andt2 to move to and fro journey respectively, the time taken by him to go downstream (while the man does not swim) is :
2t1t2t1+t2
√t21+t22
√t1t2
2t1t2t1−t2
The correct Answer is:D
velocity of man relative to water = v
Velocity of water flow = u
Velocity of man relative to ground in upstream =v−u
Velocity of man relative to ground in downstream =v+u
Now for to and fro motion, time taken to cover distance d in upstream t1=dv−u
1t1=vd−ud ...(i)
And time taken to cover distance d in downstream
t2=dv+u
1t2=vd+ud ...(ii)
Now time taken to cover distance d in downstream
When v=0
t3=du
Subtracting equation (i) from equation (ii) we get
1t2−1t1=2ud
Now put value of u/d from equation (iii)
t1−t2t1t2=2t3⇒t3=2t1t2t1−t2.
Topper's Solved these Questions
- GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONBOOK - A2ZCHAPTER - GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONEXERCISE - Understanding Motion Through Graphs
40 Videos
- GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONBOOK - A2ZCHAPTER - GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONEXERCISE - Problem Based On Mixed Concepts
30 Videos
- GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONBOOK - A2ZCHAPTER - GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONEXERCISE - Motion Under Gravity
30 Videos
- FLUID MECHANICSBOOK - A2ZCHAPTER - FLUID MECHANICSEXERCISE - Chapter Test
29 Videos
- GRAVITATIONBOOK - A2ZCHAPTER - GRAVITATIONEXERCISE - Chapter Test
29 Videos
Similar Questions
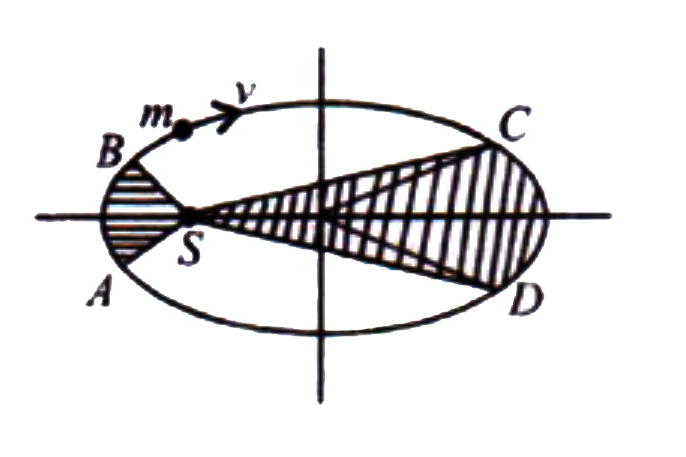
The given figure shows the elliptical orbit of a planet m about the sun S. If t1 is the time taken by the planet of move from C to D and t2 is the time taken by the planet to move from A to B, then the relation between t1andt2 is [Given, area SCD = 2 (area SAB)]
View SolutionA boy reaches the airport and finds that the escalator is not working. He walks up the stationary escalator in time t1. If the remains stationary on a moving escalator then the escalator takes him up in time t2. The time taken by him to walk up on the moving escalator will be :
View Solution
Knowledge Check
Referring to Q.95, the time taken by the man in moving to and fro through equal distance when there is no flow of water is :
At1+t22Bt1t2t1−t2C4t1t2t1+t2D√t1t2A man rows a boat upstream a certain distance and then returns back to the same place. If the time taken by him in going upstream is twice the time taken in rowing downstream, find the ratio of the speed of the boat in still water and the speed of the stream.
A2:1B3:2C5:3D3:1The time taken by a man to row downstream is 35 the of the time taken by him to row upstream. If the product of the speeds of the man and the current is (both taken in kmph) 36, then find the speed of the man and the current .
A12 kmph, 3 kmphB10 kmph, 2 kmphC9 kmph, 2 kmphD10 kmph, 3 kmph
A man can swim 5 km/h in still water if the speed of current be 3 km/h the time taken by him to swim to a palce 16 km upstream and back is:
View SolutionA man can swim 5 km/h in still water. If the speed of current be 3 km/h, the time taken by him to swim to a place 16 km upstream and back is :
View SolutionThe speed of a stream is 3 km/h and the speed of a man in still water is 5 km/h. The time taken by the man to swim 26 km downstream is :
View SolutionAt a metro station, a girl walks up a stationary escalator in time t1 If she remains stationary on the escalator, then the escalator take her up in time t2. The time taken by her to walk up the moving escalator will be.
View SolutionAt a metro station, a girl walks up a stationary escalator in time t1 If she remains stationary on the escalator, then the escalator take her up in time t2. The time taken by her to walk up the moving escalator will be.
View Solution
