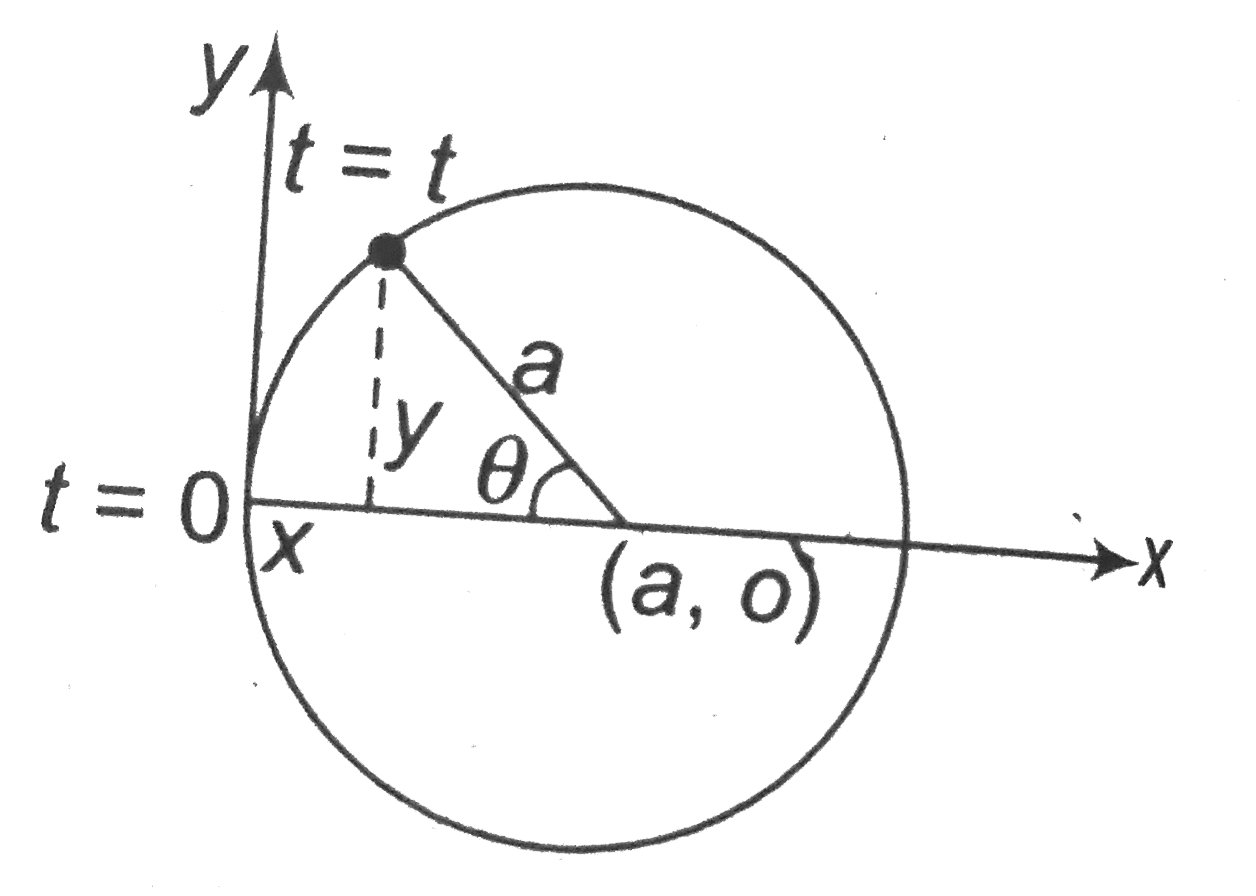
Position vectors of a particle moving in xy plane at time t is $\to r = a (1 - cos o m η t) ˆ i + a sin ω t ˆ j$ . The path of the particle is

A

a circle of radius a and center at (a,0)

B

a circle of radius a and center at (0,0)

C

an ellipse

D

neither a circle nor an ellipse

Video Solution

Text Solution

Verified by Experts

The correct Answer is:a

Particle is moving in a circle of radius 'a' and centre (a,0) with constant angular velocity $' ω'$ . At time t=0 particle is at origin and it starts rotating clockwise. At time t it has rotated an angle $θ$ given by:
$θ = ω t$
$y = a sin θ = a sin ω t$
and $x = a - a cos θ = a (1 - cos ω t)$
$∴ \to r = a (1 - cos ω t) ˆ i + a sin ω t ˆ j$

|

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Position vector of a particle moving in $x - y$ plane at time $t$ is $r = a (1 - cos ω t) ˆ i + a sin ω t ˆ j$ . The path of the particle is
Aa circle of radius a and centre and (a,0)
Ba circle of radius a and centre at (0,0)
Can ellipse
DNeither a circle nor an ellipse
Question 2 - Select One
The positoin vector of a particle is $\to r = (a cos ω t) ˆ i + (a sin ω t) ˆ j$ . The velocity of the paritcle is
AParallel to the position vector
BPerpendicular to the position vector
CDirected towards the origin
DDirected away from the origin
Question 3 - Select One
If s=a $sin ω t ˆ i + b cos ω t ˆ j$ , the equation of path of particle is
A $x^{2} + y^{2} = \sqrt{a^{2} + b^{2}}$
B $\frac{x^{2}}{b^{2}} + \frac{y^{2}}{a^{2}} = 1$
C $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$
DNone of these

A2Z-MOTION IN TWO DIMENSION-Kinematics Of Circular Motion

Home
Ask Doubt
Profile