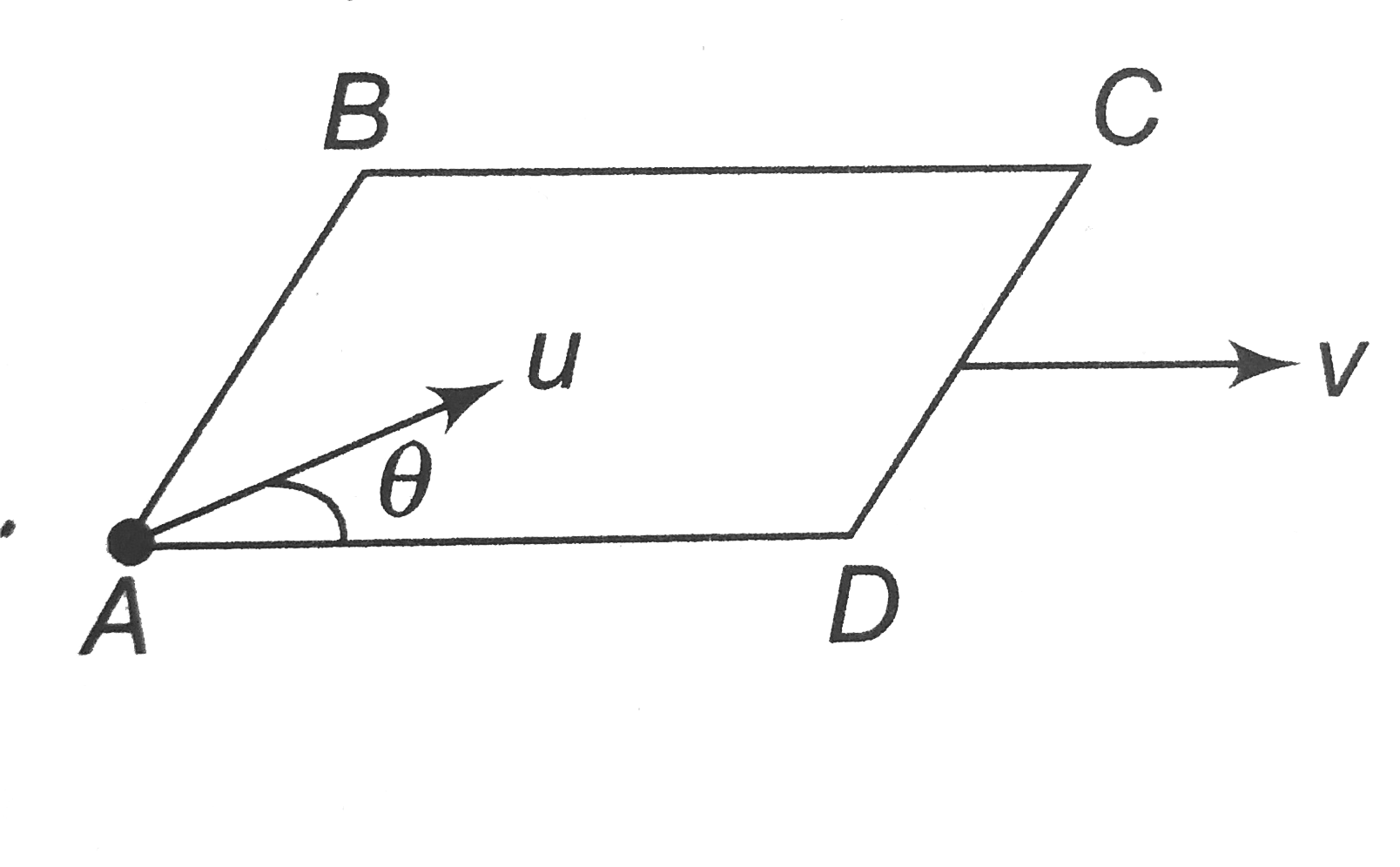
A smooth square platform ABCD is moving towards right with a uniform speed v. At what angle θ must a particle be projected from A with speed u so that it strikes the point B
sin−1(uv)
cos−1(vu)
cos−1(uv)
sin−1(vu)
The correct Answer is:b
Particle will strike the point B if velocity of particle with respect to platform is along AB or component of its relative along AD is zero.
So, ucosθ=v
or θ=cos−1(vu)
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Assertion Reasoning11videos
MOTION IN TWO DIMENSION
- BOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - NEET Questions16videos
MOTION IN TWO DIMENSION
- BOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Kinematics Of Circular Motion26videos
MOTION IN TWO DIMENSION
- BOOK - A2ZCHAPTER - MOCK TESTEXERCISE - Motion With Constant Acceleration15videos
MOCK TEST
- BOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test30videos
NEWTONS LAWS OF MOTION
Similar Questions
A particle moving in a circle of radius R with a uniform speed takes a time T to complete one revolution. If this particle were projected with the same speed at an angle θ to the horizontal, the maximum height attained by it equals 4R. The angle of projection θ is then given by
View SolutionA large wedge BCD, having its inclined surface at an angle θ=45∘ to the horizontal, is travelling horizontally leftwards with uniform velocity u=10m/s
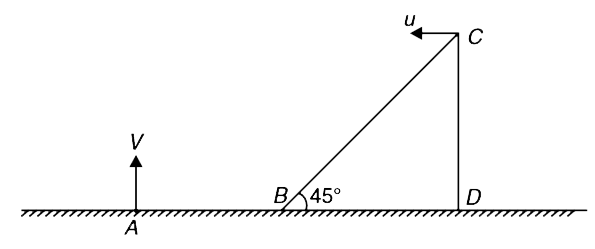
At some instant a particle is projected vertically up with speed V=20m/s from point A on ground lying at some distance right to the lower edge B of the wedge. The particle strikes the incline BC normally, while it was falling. [g=10m/s2]
(a) Find the distance AB at the instant the particle was projected from A.
(b) Find the distance of lower edge B of the wedge from point A at the instant the particle strikes the incline.
(c) Trace the path of the particle in the reference frame attached to the wedge.View Solution
Knowledge Check
- Question 1 - Select One
A large platform is moving with constant acceleration 'a' perpendicular to its plane in gravity free space. A particle of mass m is projected with speed u relative to the platform at an angle θ with its plane from a point O on it. The angular momentum of the particle about O:
AAlways increasesBAlways decreasesCFirst decreases and then increasesDFirst increases and then decreases - Question 2 - Select One or More
A particle is projected at an angle θ from ground with speed u (g = 10 m/s2 )
Aif u = 10 m/s and θ=30∘, then time of flight will be 1 secBIf u=10√3m/sandθ=60∘, then time of flight will be 3 sec.Cif u=10√3m/sandθ=60∘, then after 2 sec velocity becomes perpendicular to initial velocity.Dif u = 10 m/s and θ=30∘, then velocity never becomes perpendicular to initial velocity during its flight. - Question 3 - Select One
A particle is moving in a circle with uniform speed v . In moving from a point to another diametrically opposite point
AThe momentum changes by mvBThe momentum changes by 2mvCThe kinetic energy changes by (1/2)mvDThe kinetic energy changes by mv2
A particle strikes a horizontal frictionless floor with a speed u, at an angle θ to the vertical, and rebounds with a speed v, at an angle ϕ to the vertical. The coefficient of restitution between the particle and the floor is e. The magnitude of v is
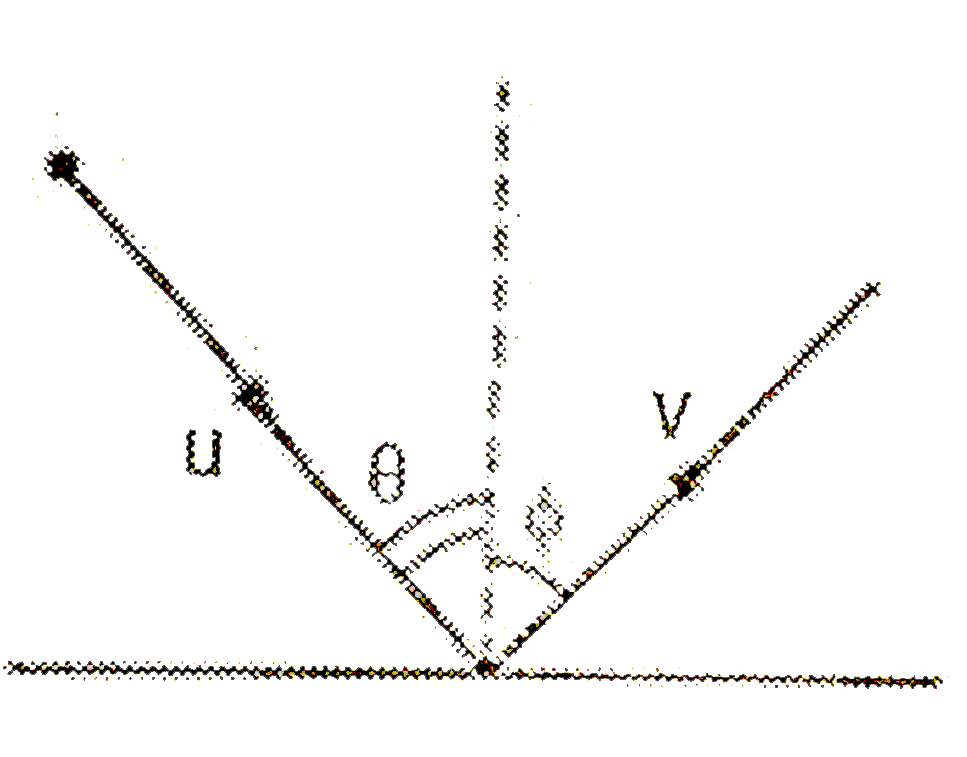 View Solution
View SolutionA particle strikes a horizontal frictionless floor with a speed u, at an angle θ with the vertical, and rebounds with a speed υ, at an angle ϕ with the vertical. The coefficient of restitution between the particle and the floor is e. The angle ϕ is equal to :
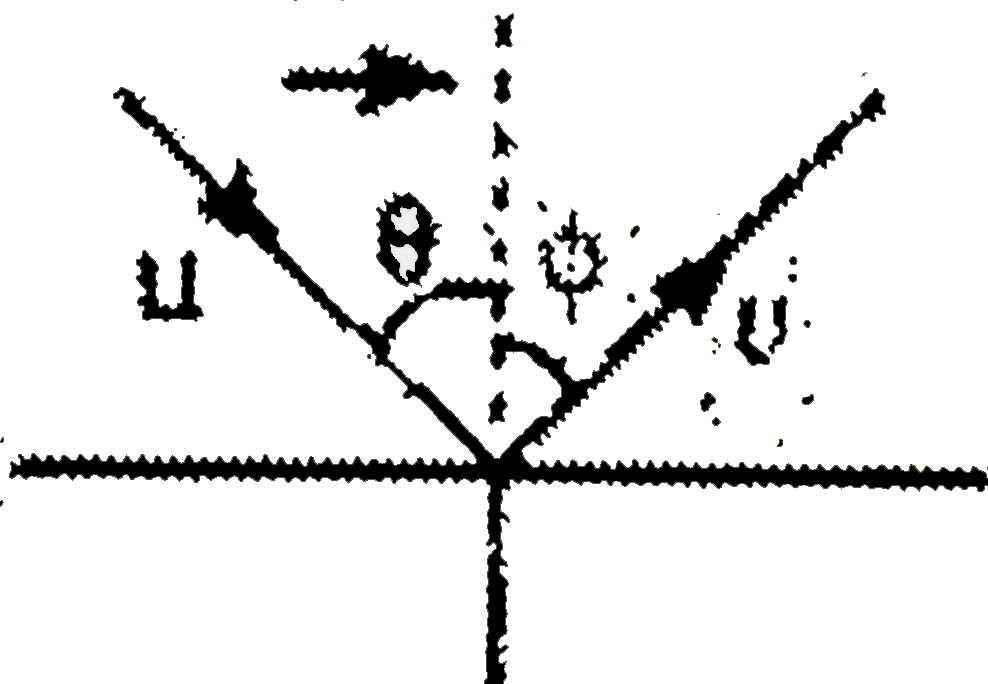 View Solution
View SolutionA particle moving with a speed v changes direction by an angle θ, without change in speed.
View SolutionA particle strikes a horizontal frictionless floor with a speed u at an angle θ with the vertical, and rebounds with a speed v at an angle ϕ with vertical. The coefficient of restitution between the particle and floor is e. The magnitude of v is
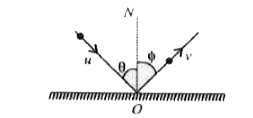 View Solution
View SolutionA particle strikes a horizontal frictionless floor with a speed u at an angle θ with the vertical, and rebounds with a speed v at an angle ϕ with vertical. The coefficient of restitution between the particle and floor is e. The angle ϕ is equal to
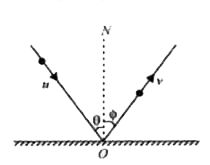 View Solution
View Solution

