A uniform rod of length 1m mass 4kg is supports on two knife-edges placed 10cm from each end. A 60N weight is suspended at 30cm from one end. The reactions at the knife edges is.
60 N, 40 N
75 N, 25 N
65 N, 35 N
55 N, 45 N
The correct Answer is:C
To solve the problem, we need to find the reactions at the two knife edges supporting the uniform rod. We will follow these steps:
Step 1: Understand the Setup
We have a uniform rod of length 1 m and mass 4 kg, which means its weight (W_rod) is:
Wrod=mass×g=4kg×9.81m/s2=39.24N
The rod is supported on two knife edges placed 10 cm from each end. A 60 N weight is suspended at a distance of 30 cm from one end of the rod.
Step 2: Identify Forces and Distances
- Let the left end of the rod be point A and the right end be point B.
- The knife edges are at points C (10 cm from A) and D (10 cm from B).
- The suspended weight (60 N) is at a distance of 30 cm from A, which means it is at point E (30 cm from A).
Step 3: Calculate Total Weight
The total downward force acting on the rod is the sum of the weight of the rod and the suspended weight:
Ftotal=Wrod+Wsuspended=39.24N+60N=99.24N
Step 4: Set Up Equations for Equilibrium
For the rod to be in equilibrium, the sum of vertical forces must be zero:
R1+R2=99.24N (Equation 1)
Where R1 is the reaction at knife edge C and R2 is the reaction at knife edge D.
Step 5: Calculate Moments about a Point
To find the reactions, we can take moments about one of the knife edges. Let's take moments about point C.
The moment due to the weight of the rod acts at its center of mass, which is at 50 cm from A (or 40 cm from C). The moment due to the suspended weight acts at 20 cm from C (30 cm from A - 10 cm from C).
The clockwise moments must equal the counterclockwise moments about point C:
60N×20cm+39.24N×40cm=R2×80cm
Step 6: Substitute and Solve for R2
Convert cm to m for calculations:
60×0.20+39.24×0.40=R2×0.80
12+15.696=R2×0.80
27.696=R2×0.80
R2=27.6960.80=34.62N
Step 7: Substitute R2 back into Equation 1 to find R1
Using Equation 1:
R1+34.62=99.24
R1=99.24−34.62=64.62N
Final Answer
The reactions at the knife edges are:
- R1≈64.62N
- R2≈34.62N
We have a uniform rod of length 1 m and mass 4 kg, which means its weight (W_rod) is:
Wrod=mass×g=4kg×9.81m/s2=39.24N
- Let the left end of the rod be point A and the right end be point B.
- The knife edges are at points C (10 cm from A) and D (10 cm from B).
- The suspended weight (60 N) is at a distance of 30 cm from A, which means it is at point E (30 cm from A).
The total downward force acting on the rod is the sum of the weight of the rod and the suspended weight:
Ftotal=Wrod+Wsuspended=39.24N+60N=99.24N
For the rod to be in equilibrium, the sum of vertical forces must be zero:
R1+R2=99.24N (Equation 1)
To find the reactions, we can take moments about one of the knife edges. Let's take moments about point C.
60N×20cm+39.24N×40cm=R2×80cm
Convert cm to m for calculations:
60×0.20+39.24×0.40=R2×0.80
12+15.696=R2×0.80
27.696=R2×0.80
R2=27.6960.80=34.62N
Using Equation 1:
R1+34.62=99.24
R1=99.24−34.62=64.62N
The reactions at the knife edges are:
- R1≈64.62N
- R2≈34.62N
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Angular Momentum And Its Conservation30videos
ROTATIONAL DYNAMICS
- BOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Work And Energy In Case Of Rotation22videos
ROTATIONAL DYNAMICS
- BOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Rotational Kinematics19videos
ROTATIONAL DYNAMICS
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test29videos
PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Chapter Test30videos
THERMAL PROPERTIES OF MATTER
Similar Questions
A metal bar 70cm long and 4.00kg in mass is supported on two knife edges placed 10cm from each end. A 6.00kg weight is suspended at 30cm from one end. Find the reactions at the knife edges. Assume the bar to be of uniform cross-section and homogeneous.
View SolutionA metal rod of length 50cm having mass 2kg is supported on two edges placed 10cm from each end. A 3kg load is suspended at 20cm from one end. Find the reactions at the edges (take g=10m/s2)
View Solution
Knowledge Check
- Question 1 - Select One
One end of uniform wire of length L and of weight W is attached rigidly to a point in the roof and a weight N is suspended from its lower end if s is the area of cross-section of the wire the stress in the wire at a height L4 from its lower end is
AW1sB[W1+W4]sC[W1+3W4]sDW1+W4 - Question 2 - Select One
A uniform rod is 4m long and weights 10kg. If it is supported on a kinetic edge at one meter from the end, what weight placed at that end keeps the rod horizontal.
A8kgB10kgC12kgD15kg - Question 3 - Select One
A rigid massless rod AB of length 1m is placed horizontally on two rigid supports at its ends as showm in figure. A weight 10N is hung from a point C at a distance 30cm from A. Find the reactions at the supports A and B respectively.
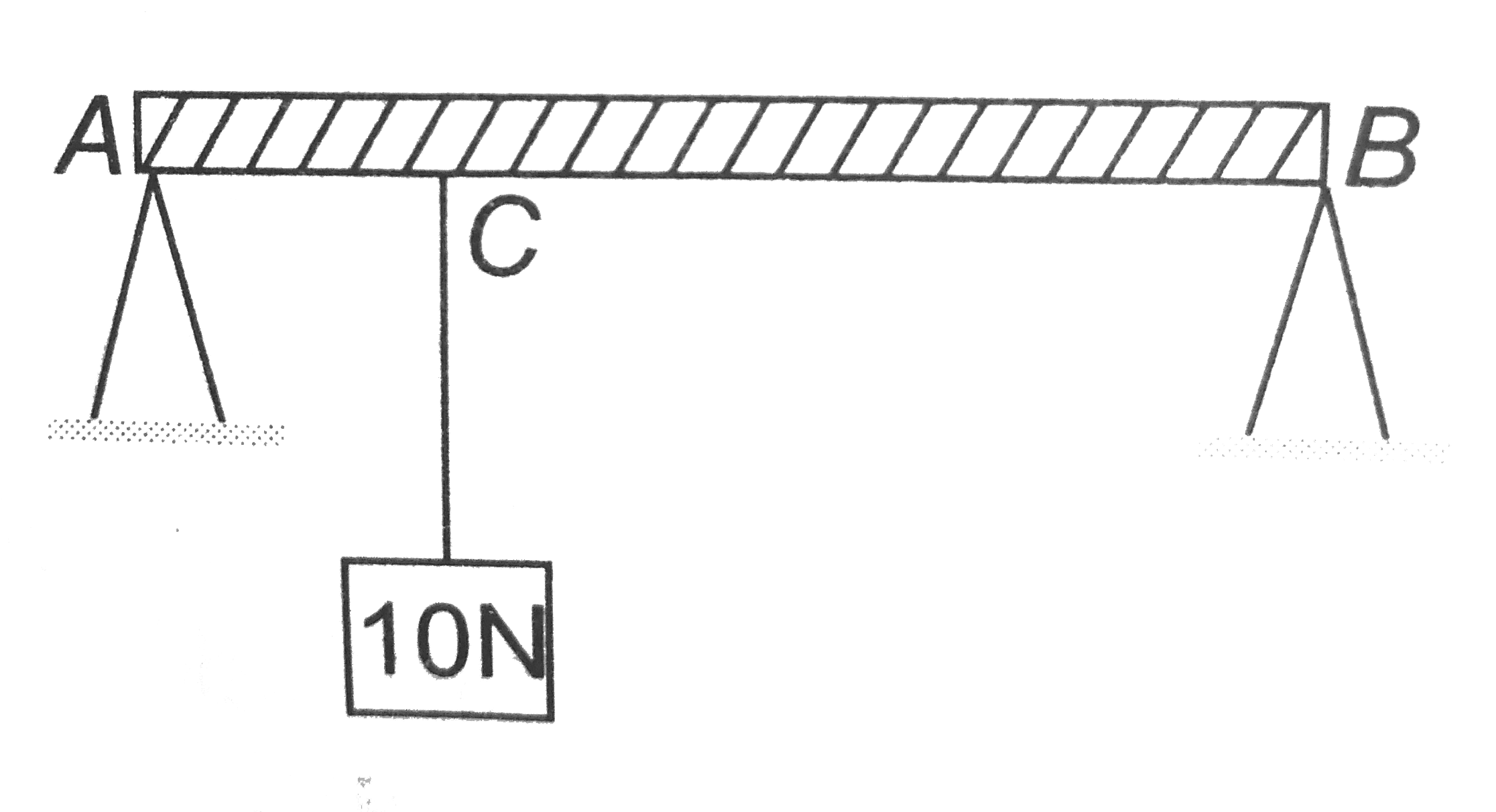 .A5 N, 5 NB3 N, 7 NC10 N, 0 ND7 N, 3 N
.A5 N, 5 NB3 N, 7 NC10 N, 0 ND7 N, 3 N
A uniform rod of length 200cm and mass 500g is balanced on a wedge placed at 40 cm mark. A mass of 2Kg is suspended from the rod at 20cm and another unknown mass m is suspended from the rod at 160cm mark as shown in figure. Find value of m such that the rod is in equilibrium.
 View Solution
View SolutionA uniform rod of length L (in between the supports) and mass m is placed on two support A and B. The rod breaks suddenly at length L/10 from the support B. Find the reaction at support A immediately after the rod breaks
 View Solution
View SolutionOne end of a uniform bar of weight w1 is suspended from the roof and a weight w2 is suspended from the other end, the area of cross-section is A. What is the stress at the midpoint of the rod ?
View SolutionOne end of a uniform bar of weight w1 is suspended from the roof and a weight w2 is suspended from the other end, the area of cross-section is A. What is the stress at the midpoint of the rod ?
View SolutionThe uniform 120N board shown in figure is supported by two ropes. A 400N weight is suspended one-fourth of the way from the left end. Choose the correct options
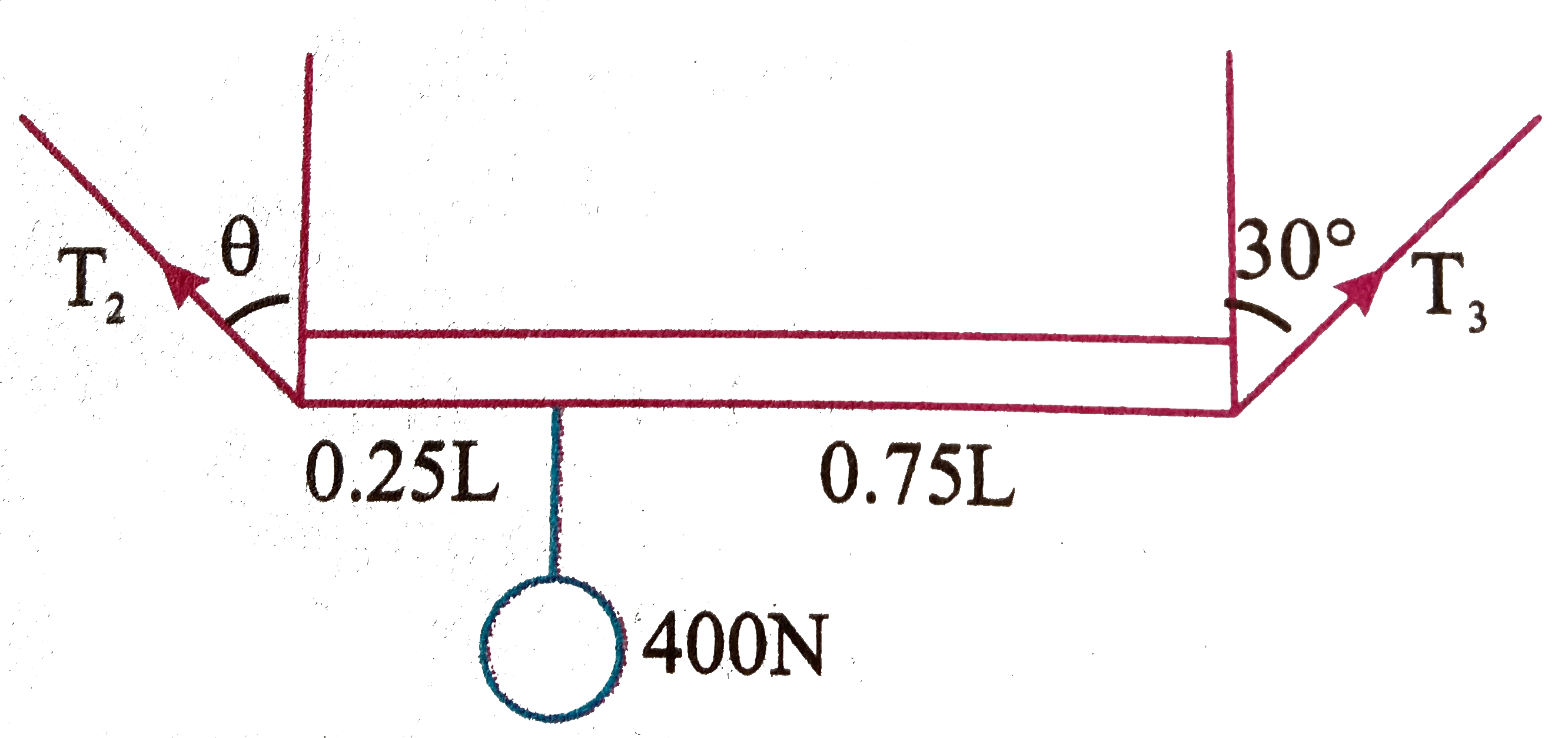 View Solution
View Solution

