A disk with moment of inertia I1 rotates about frictionless, vertical axle with angular speed ωi A second disk, this one having moment of inertia I2 and initial not rotating, drops onto the first disk (Fig.) Because of friction between the surfaces, the two eventually reach the same angular speed ωf. The value of ωf is.
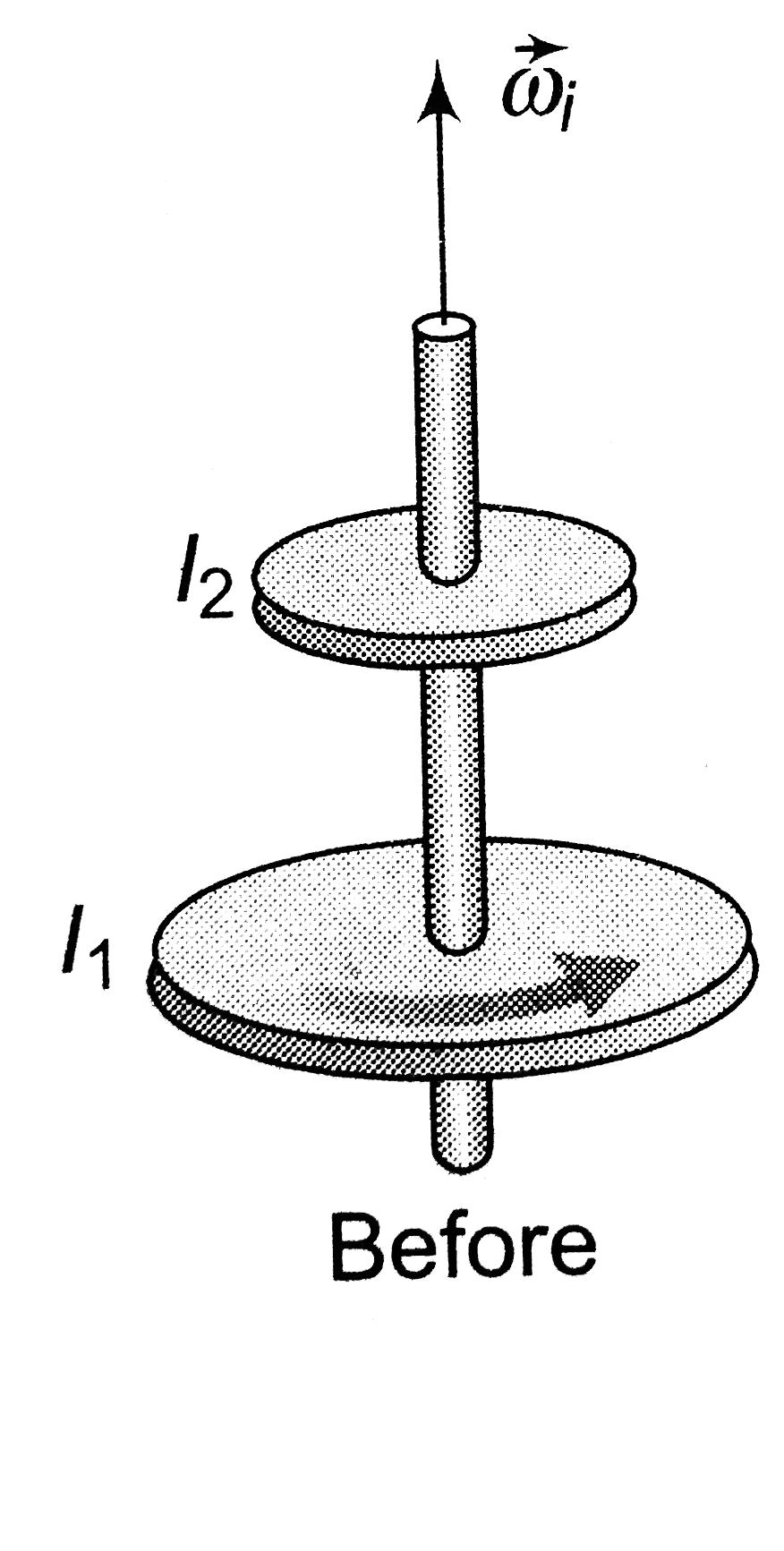 .
.
I1+I2I1ωi
I1I1+I2ωi
I1+I2I2ωi
I1I2ωi
The correct Answer is:B
(b) From conservation of angular momentum for the isolated system of two disks :
(I1+I2)ωf=Iiωi or ωf=I1I1+I2ωi.
Topper's Solved these Questions
- ROTATIONAL DYNAMICSBOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Work And Energy In Case Of Rotation
22 Videos
- ROTATIONAL DYNAMICSBOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Rotation And Translation Combined And Rolling Motion
18 Videos
- ROTATIONAL DYNAMICSBOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Torque , Torque Equation And Equilibrium Of A Rigid Body
29 Videos
- PROPERTIES OF MATTERBOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test
29 Videos
- THERMAL PROPERTIES OF MATTERBOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Chapter Test
30 Videos
Similar Questions
A disc of moment of inertia I1 is rotating freely with angular speed ω1 when another non-rotating disc of moment of inertia I2 is dropped on it. The two discs then rotate as one unit. Find the final angular speed.
View SolutionA disc with moment of inertial I is rotating with some angular speed. Second disc is initially at rest. Now second disc with moment of inertia 3I is placed on first disc and starts rotating. Find loss of kinetic energy in fraction
View Solution
Knowledge Check
A circular disk of moment of inertia It is rotating in a horizontal plane , about its symmetry axis , with a constant angular speed ωi . Another disk of moment of inertia Ib is dropped coaxially onto the rotating disk . Initially the second disk has zero angular speed . eventually both the disks rotate with a constant angular speed ωf . The energy lost by the initially rotating disc to friction is
A12I2b(It+Ib)ω2iB12I2t(Ii+Ib)ω2iCIb−It(It+Ib)ω2iD12IbIt(It+Ib)ω2iA disc of moment of inertia I1 is rotating freely with angular speed ω1 when another non-rotating disc of moment of inertia I2 is dropped on it. The two discs then rotate as one unit. Find the final angular speed.
AI1ω1I2BI2ω1I2+I2CI1ω2I1+I2D(I1+I2)I2ω1A torque T acts on a body of moment of inertia l rotating with angular speed ω. It will be stopped just after time
AlTωBlωTCTωlDlωT
A circular disc of moment of inertia It is rotating in a horizontal plane about its symmetry axis with a constant angular velocity ωi. Another disc of moment of inertia Ib is dropped co-axially onto the rotating disc. Initially, the second disc has zero angular speed. Eventually, both the discs rotate with a constant angular speed ωf. Calculate the energy lost by the initially rotating disc due to friction.
View SolutionA wheel of moment of inertial I and radius R is rotating about its axis at an angular speed ω. It picks up a stationary particle of mass m at its edge. Find the new angular speed of the wheel.
View SolutionA disc with moment of inertiaI1, is rotating with an angular velocity ω1 about a fixed axis. Another coaxial disc with moment of inertia I2, which is at rest is gently placed on the first disc along the axis. Due to friction discs slips against each other and after some time both disc start rotating with a common angular velocity. Find this common angular velocity.
View SolutionTwo bodies have their moments of inertia I and 2I respectively about their axis of rotation. If their kinetic energies of rotation are equal, their angular momenta will be in the ratio.
View SolutionTwo bodies have their moments of inertia I and 2I respectively about their axis of rotation. If their kinetic energies of rotation are equal, their angular momenta will be in the ratio.
View Solution
