Three liquids of densities ρ1,ρ2 and ρ3 (with ρ1>ρ2>ρ2) having the same value of surface tension T, rise to the same height in three identical capillaries. The angles of contact θ1,θ2 and θ3 obey
π2<θ1<θ2<θ<π
π>θ1>θ2>θ3>π2
π2>θ1>θ2>θ3≥0
0≤θ1<θ2<θ3<π2
The correct Answer is:D
To solve the problem, we need to analyze the relationship between the angles of contact (θ₁, θ₂, θ₃) of three liquids with different densities (ρ₁, ρ₂, ρ₃) that rise to the same height in identical capillaries.
1. Understanding Capillary Rise: The height of liquid rise in a capillary tube is given by the formula:
h=2Tcosθρgr
where:
- h = height of the liquid column,
- T = surface tension,
- θ = angle of contact,
- ρ = density of the liquid,
- g = acceleration due to gravity,
- r = radius of the capillary tube.
2. Identifying Constants: Since all three liquids rise to the same height h in identical capillaries, we can rearrange the formula to express cosθ:
cosθ=ρgrh2T
Here, grh2T is a constant for all three liquids.
3. Analyzing Density and Cosine Relationship: From the rearranged equation, we see that:
cosθ∝ρ
This means that as the density increases, the value of cosθ also increases.
4. Relating Angles of Contact: Since cosθ is directly proportional to the density:
- For the highest density liquid (ρ₁), cosθ1 will be the largest, which means θ1 will be the smallest.
- For the medium density liquid (ρ₂), cosθ2 will be smaller than cosθ1, meaning θ2 will be larger than θ1.
- For the lowest density liquid (ρ₃), cosθ3 will be the smallest, which means θ3 will be the largest.
5. Conclusion: Therefore, we can conclude the order of angles of contact:
θ1<θ2<θ3
This indicates that the angle of contact increases as the density of the liquid decreases.
Final Answer:
The angles of contact obey the relation:
θ1<θ2<θ3
h=2Tcosθρgr
where:
- h = height of the liquid column,
- T = surface tension,
- θ = angle of contact,
- ρ = density of the liquid,
- g = acceleration due to gravity,
- r = radius of the capillary tube.
cosθ=ρgrh2T
Here, grh2T is a constant for all three liquids.
cosθ∝ρ
This means that as the density increases, the value of cosθ also increases.
- For the highest density liquid (ρ₁), cosθ1 will be the largest, which means θ1 will be the smallest.
- For the medium density liquid (ρ₂), cosθ2 will be smaller than cosθ1, meaning θ2 will be larger than θ1.
- For the lowest density liquid (ρ₃), cosθ3 will be the smallest, which means θ3 will be the largest.
θ1<θ2<θ3
This indicates that the angle of contact increases as the density of the liquid decreases.
The angles of contact obey the relation:
θ1<θ2<θ3
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - AIIMS Questions41videos
PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test29videos
PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Assertion Reasoning20videos
PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Chapter Test29videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Chapter Test29videos
ROTATIONAL DYNAMICS
Similar Questions
A liquid of density ρ and surface tension S rises to a height h in a capillary tube of diameter D. what is the weight of the liquid in the capillary tube? Angle of contact is 0∘.
View SolutionWhen a capillary tube of radius r is dipped vertically in a liquid of surface tension T, the liquid rises to a height h in the tube above the level outside the tube . If the angle of contact is θ the density of the liquid is ρ then the pressure difference between the points A and B is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Three liquids of densities ρ1,ρ2 and ρ3 (with ρ1>ρ2>ρ3), having the same value of surface tension T, rise to the same height in three identical capillaries. The angles of contact θ1,θ2 and θ3 obey
Aπ2>θ1>θ2>θ3≥0B0≤θ1<θ2<θ3<π2Cπ2<θ1<θ2<θ3<πDπ>θ1>θ2>θ3>π2 - Question 2 - Select One
Three liquids of densities ρ1,ρ2 and ρ3 (with ρ1>ρ2>ρ3), having the same value of surface tension T, rise to the same height in three identical capillaries. The angles of contact θ1,θ2 and θ3 obey
Aπ2<θ1<θ2<θ3<πBπ>θ1>θ2>θ3>π2Cπ2>θ1>θ2>θ3≥0D0≤θ1<θ2<θ3<π2 - Question 3 - Select One
Three liquids of densities ρ1,ρ2 and ρ3 (with ρ1>ρ2>ρ3), having the same value of surface tension T, rise to the same height in three identical capillaries. The angles of contact θ1,θ2 and θ3 obey
Aπ2<θ1<θ2<θ3<πBπ>θ1>θ2>θ3>π2Cπ2>θ1>θ2>θ3≥0D0≤θ1<θ2<θ3<π2
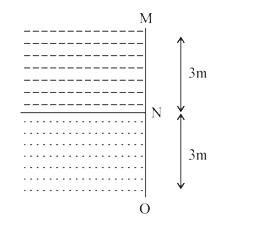
Two liquids of densities ρ1 and ρ2(ρ2=3ρ1) are filled up behind a square wall of side 6 m as shown in figure. Each liquid has a height of 3 m. The ratio of the forces due to these liquids exerted on upper part MN to that at the lower part NO is (Assume that the liquids are not mixing)2
 View Solution
View SolutionThe potential energy of the liquid of surface tension T and density ρ that rises into the capillary tube is
View SolutionIf two liquids of same mass but densities ρ1 and ρ2 respectively are mixed, then the density of the mixture is:
View SolutionIf two liquids of same masses but densities ρ1andρ2 respectively are mixed, then the density of mixture is given by
View SolutionTwo liquids of densities 2ρ and ρ having their volumes in the ratio 3:2 are mixed together. Density of the mixture will be
View Solution

