A block of mass 2kg executes simple harmonic motion under the reading from at a spring .The angular and the time period of motion are 0.2cm and 2πsec respectively Find the maximum force execute by the spring in the block.
0.05N
0.002N
0.003N
0.004N
The correct Answer is:D
To find the maximum force exerted by the spring on the block executing simple harmonic motion, we can follow these steps:
Step 1: Identify the given values
- Mass of the block, m=2kg
- Amplitude of motion, A=0.2cm=0.002m (convert cm to m)
- Time period of motion, T=2πs
Step 2: Calculate the angular frequency (ω)
The angular frequency is given by the formula:
ω=2πT
Substituting the value of T:
ω=2π2π=1rad/s
Step 3: Calculate the maximum force (Fmax)
The maximum force exerted by the spring can be calculated using the formula:
Fmax=mω2A
Substituting the values we have:
Fmax=2kg×(1rad/s)2×0.002m
Fmax=2×1×0.002=0.004N
Conclusion
The maximum force exerted by the spring on the block is 0.004N.
---
- Mass of the block, m=2kg
- Amplitude of motion, A=0.2cm=0.002m (convert cm to m)
- Time period of motion, T=2πs
The angular frequency is given by the formula:
ω=2πT
Substituting the value of T:
ω=2π2π=1rad/s
The maximum force exerted by the spring can be calculated using the formula:
Fmax=mω2A
Substituting the values we have:
Fmax=2kg×(1rad/s)2×0.002m
Fmax=2×1×0.002=0.004N
The maximum force exerted by the spring on the block is 0.004N.
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Spring Particle System24videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Simple Pendulum And Different Cases Of Shm25videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Chapter Test29videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test30videos
NEWTONS LAWS OF MOTION
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test29videos
PROPERTIES OF MATTER
Similar Questions
A block of mass 5 kg executes simple harmonic motion under the restoring force of a spring. The amplitude and the time period of the motion are 0.1 m and 3.14 s respectively. Fnd the maximum force exerted by the spring on the block.
View SolutionA body of mass 0.01 kg executes simple harmonic motion about x = 0 under the influence of a force as shown in figure. The time period of SHM is
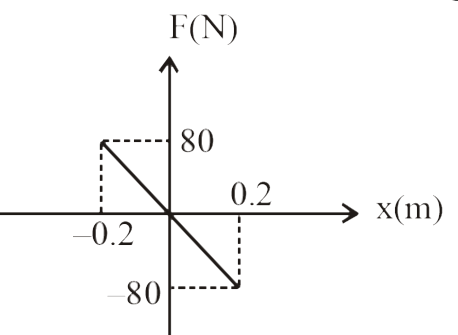 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass 2 kg executes SHM on a smooth horizontal plane under the action of restoring force of a spring. If the amplitude and time period of oscillation are 0.05 m and π/5 second, the maximum force exerted by the spring on the block is
A5 NB10 NC100 ND19.6 N - Question 2 - Select One
A body of mass 0.01 kg executes simple harmonic motion (SHM) about x=0 under the influence of a force shown in the figure. The period of the SHM is
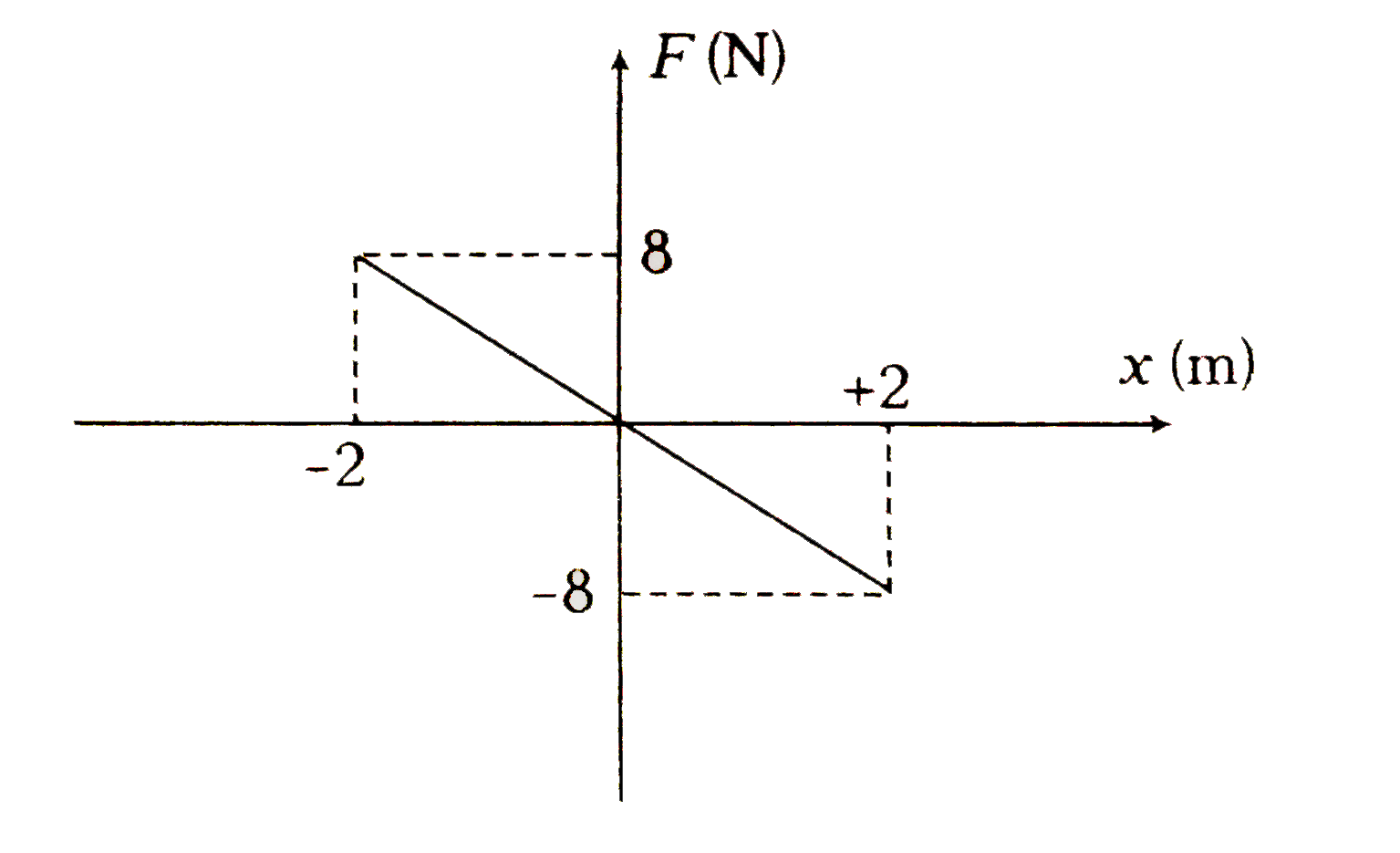 A1.05 sB0.52 sC0.25 sD0.31 s
A1.05 sB0.52 sC0.25 sD0.31 s - Question 3 - Select One or More
The phase of a particle executing simple harmonic motion is π2 when it has
AMaximum velocityBMaximum accelerationCMaximum energyDMaximum displacement
A block of mass 0.5 kg hanging from a vertical spring executes simple harmonic motion of amplitude 0.1 m and time period 0.314s. Find the maximum fore exerted by the spring on the blockl.
View SolutionA paricle of mass 200g executes a simple harmonic motion. The restorting force is provided by a spring of spring constant 80N/m. Find the time period.
View SolutionA particle executes simple harmonic motion according to equation 4d2xdt2+320x=0. Its time period of oscillation is :-
View SolutionA particle executes simple harmonic motion under the restoring force provided by a spring. The time period is T. If the spring is divided in two equal parts and one part isused to continue the simple harmonic motion, the time period will
View SolutionA particle executes simple harmonic motion. The amplitude of vibration of particle is 2 cm. The displacement of particle in one time period is
View Solution

