The resultant of two rectangular simple harmonic motion of the same frequency and unequal amplitude but differing in phase by π/2 is
Simple harmonic
Circular
Elliptical
Parabolic
The correct Answer is:C
If first equation is y1=a1sinωt
⇒sinωt=y1a1
then second equation will be
y2=a2sin(sinωtcos(π)2)
=a2[sinωtcos(pi)/(2)+ cos omega t sinπ2]=a2cosωt
⇒cosωt=y2a2
By squiring and adding (i) and (ii)
sin2ωt+cos2ωt=y21a21+y22a22
⇒y21a21+y22a22=1. This is the equation of ellipse
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - AIIMS Questions24videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Chapter Test29videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning22videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test30videos
NEWTONS LAWS OF MOTION
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test29videos
PROPERTIES OF MATTER
Similar Questions
A particle is subjected to two simple harmonic motions of the same frequency and direction. The amplitude of the first motion is 4.0cm and that of the second is 3.0cm. Find the resultant amplitude if the phase difference between the two motion is
(a) 0∘
(b) 60∘
( c) 90∘
(d) 180∘View SolutionHow are vibratory motion and simple harmonic motion different?
View Solution
Knowledge Check
- Question 1 - Select One
The resultant of two rectangular simple harmonic motion of the same frequency and unequal amplitude but differing in phase by π/2 is
ASimple harmonicBCircularCEllipticalDParabolic - Question 2 - Select One
When two mutually perpendicular simple harmonic motions of same frequency, amplitude and phase are susperimposed
Athe resulting motion is uniform circular motion.Bthe resulting motion is a linear simple harmonic motions along a straight ine inclined equally to the straight lines of motion of component ones.Cthe resulting motion is an elliptical motion, susmmetical about the lines of motion of the compounents.Dthe two S.H.M. will cancel each other. - Question 3 - Select One
A particle is subjected to two simple harmonic motions in the same direction having equal amplitudes and equal frequency. If the resulting amplitude is equal to the amplitude of individual motions, the phase difference between them is
Aπ3B2π3Cπ)6Dπ2
How are vibratory motion and simple harmonic motion different?
View SolutionThe maximum seperation between two particles executing simple harmonic motion of the equal amplitude and same frequency along the same straight line and about the same mean position, is √3 times the amplitude of oscillation. IF the phase difference between them is ϕ, determine 2π/ϕ.
View SolutionFind the phase difference between two particles executing simple harmonic motion with the same frequency if they are found inn the states shown in the figures at four different points of time.
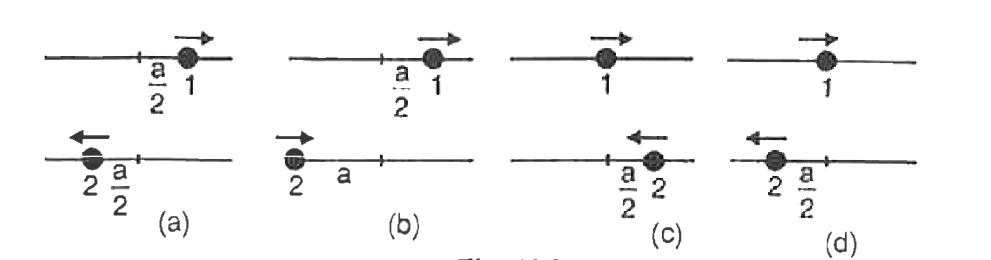 View Solution
View SolutionA particle is subjected to two simple harmonic motions in the same direction having equal amplitude and equal frequency. If the resultant amplitude is equal to the amplitude of individual motions, what is the phase difference between the motions.
View SolutionA particle is subjected to two simple harmonic motion in the same direction having equal amplitudes and equal frequency. If the resultant amplitude is equal to the amplitude of the individual motions. Find the phase difference between the individual motions.
View Solution

