The equation of displacement due to a sound wave is s=[s0sin2(ωt−kx)]if the bulk modulus of the medium is B, then the equation of pressure variation due to that sound is
Bks0sin(2ωt−2kx)
−Bks0sin(2ωt−2kx)
Bks0cos2(ωt−kx)
−Bks0cos2(ωt−kx)
The correct Answer is:A
The equation of pressure variation due to sound is
p=−Bdsdx=−ddx[s0sin2(ωt−kx)]
=Bks0sin(2ωt−2kx)
Topper's Solved these Questions
- WAVES AND ACOUSTICSBOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Doppler Effect
25 Videos
- WAVES AND ACOUSTICSBOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Problems Based On Mixed Concepts
15 Videos
- WAVES AND ACOUSTICSBOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Vibration Of Air Column
23 Videos
- VECTORSBOOK - A2ZCHAPTER - VECTORSEXERCISE - Chapter Test
29 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Chapter Test
29 Videos
Similar Questions
Corresponding to displacement equation,
y=Asin(kx+ωt)
of a longitudinal wave make its pressure and density wave also. Bulk modulus of the medium is B and density is p.
View SolutionSpeed of sound wave in a fluid depends upon Directly on density of the medium Square of bulk modulus of the medium Inversely on the square root of density Directly on the square root of bulk modulus of the medium
View Solution
Knowledge Check
The equation of a sound wave is y=0.0015sin(62.4x+316t) the wavelength of this wave is
A0.2unitB0.1unitC0.3unitDcannot the calcualtedA sound wave y=Asin(ωt−kx) is propagating through a medium of density 'ρ'. Then the sound energy per unit volume is
A1/2ρω2A2BρA2ω2C2ρA2ω2D4ρA2ω2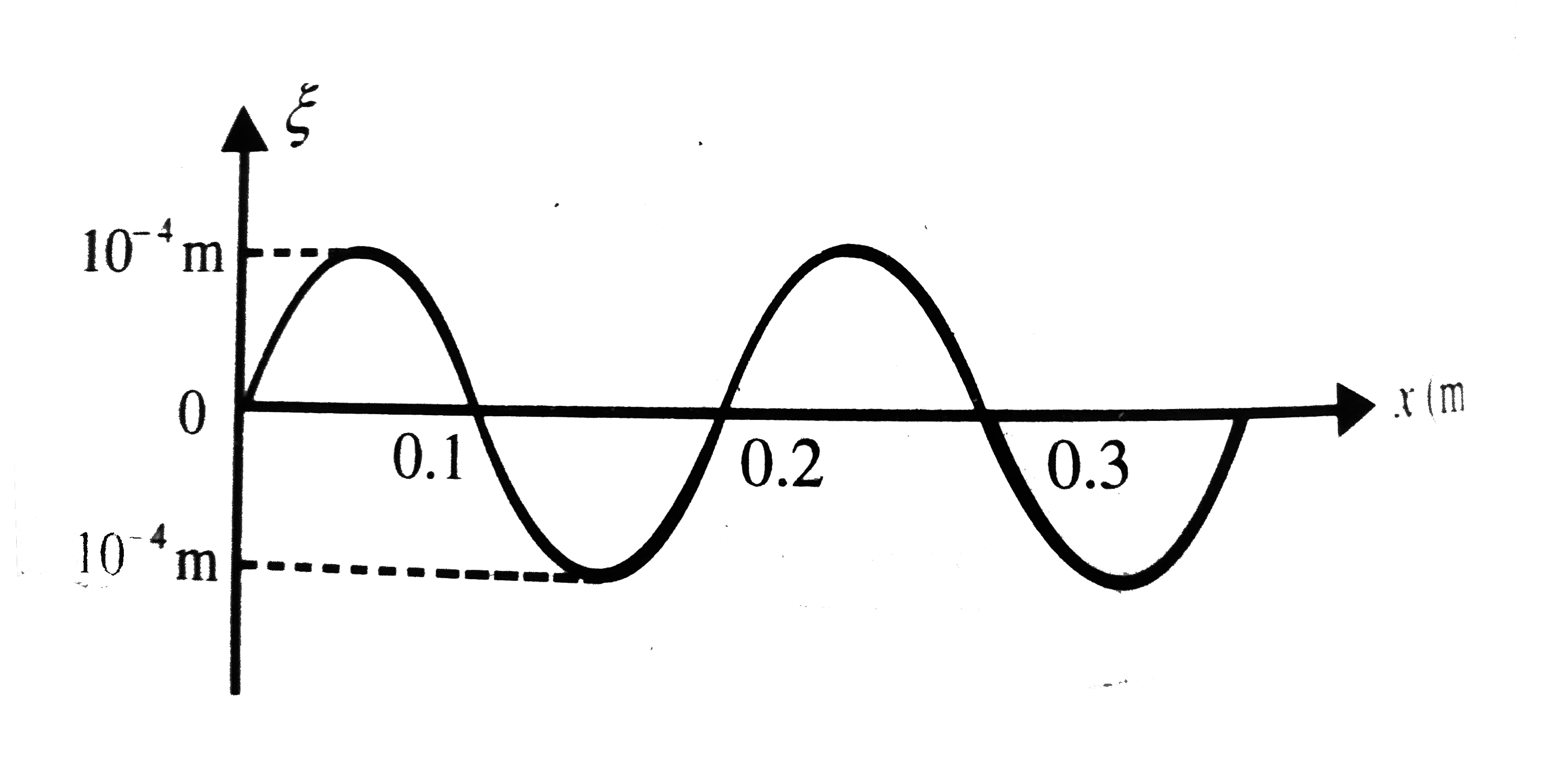
For a sound wave travelling towards +x direction, sinusoidal longitudinal displacement ε at a certain time is given as a function of x (Fig). If bulk modulus of air is B=5×105Nm2, the variation of pressure excess will beA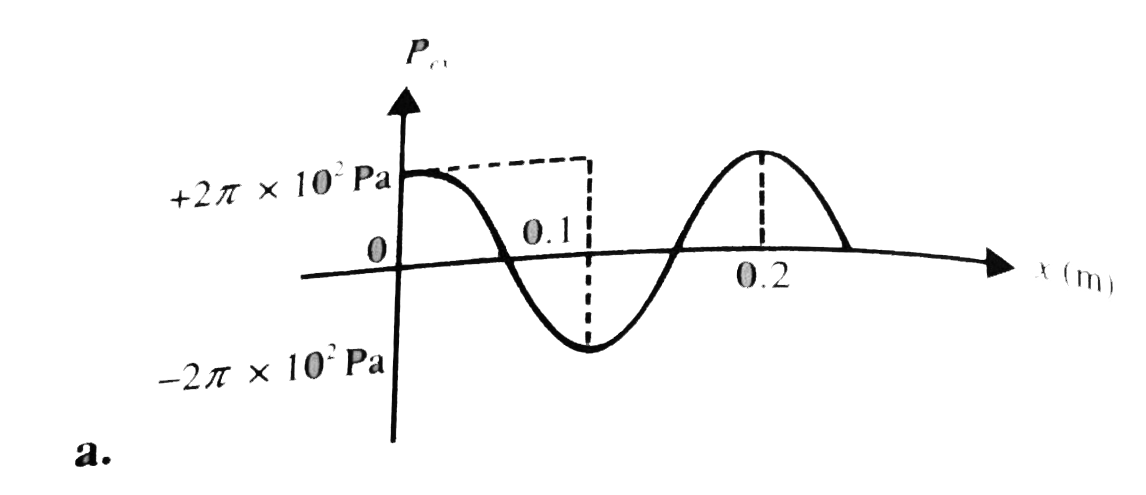 B
B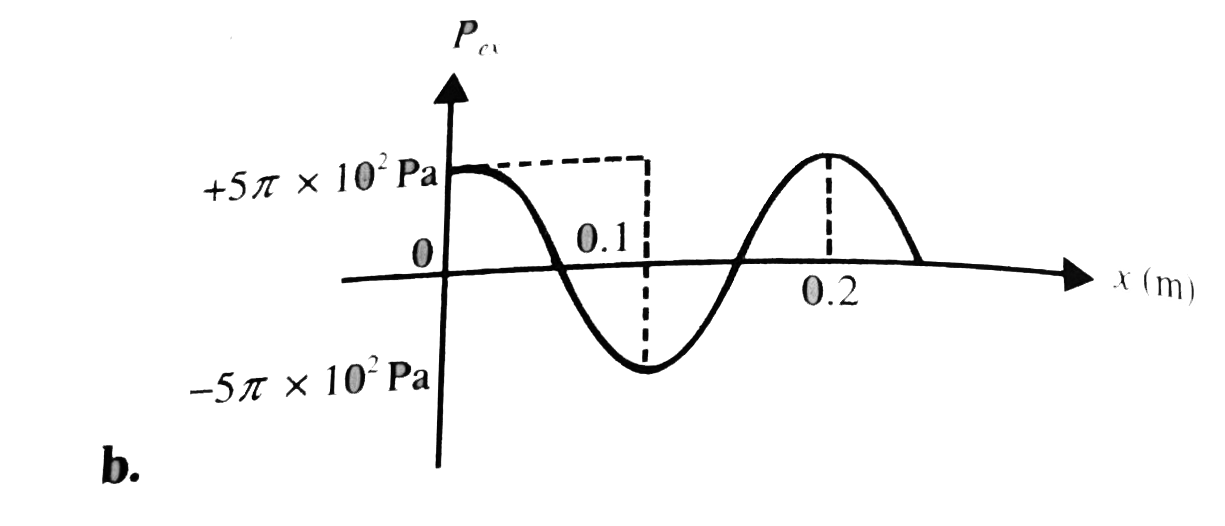 C
C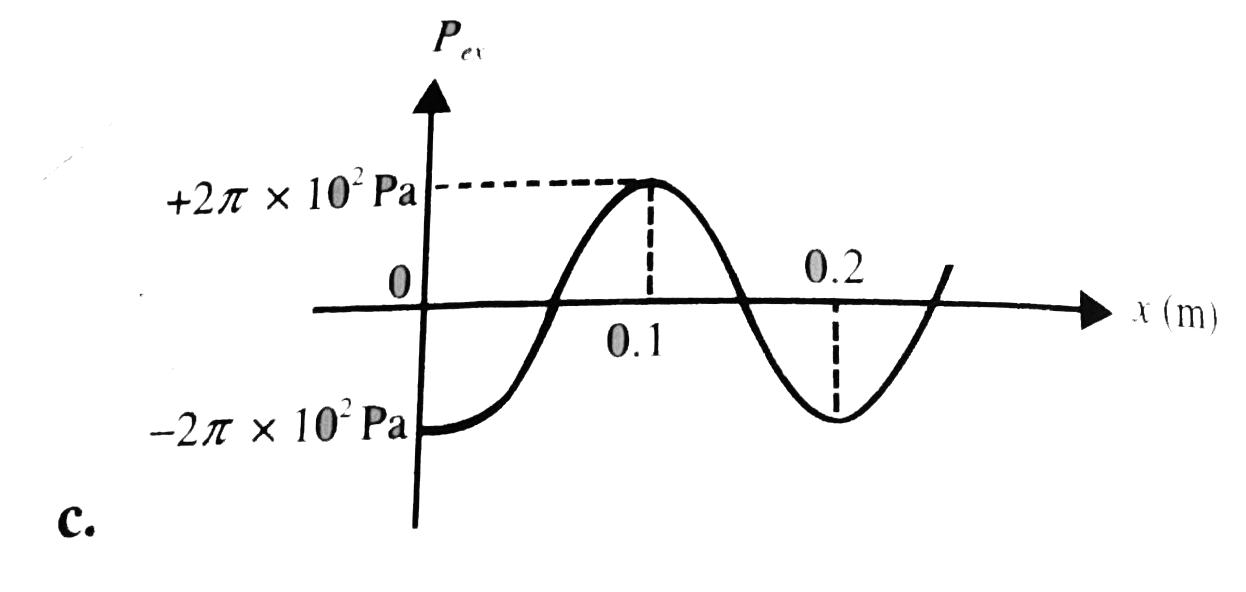 D
D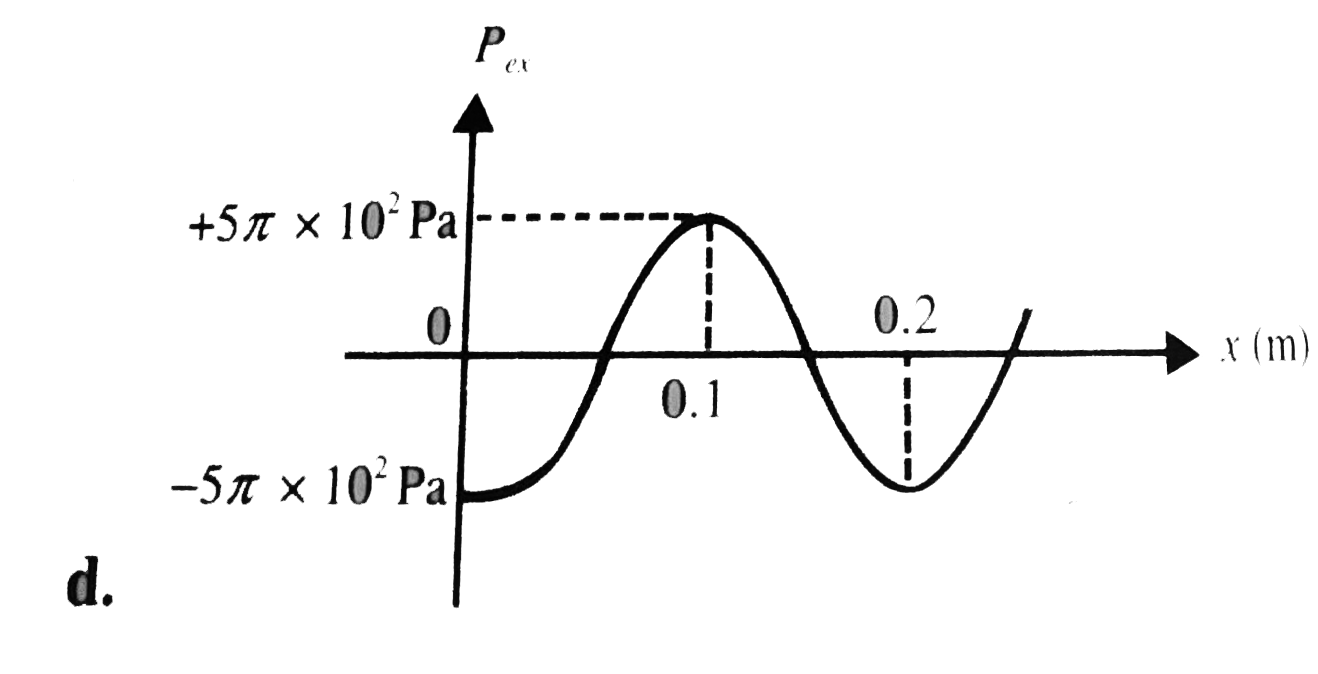
A sound wave is travelling in a medium.If equation of displacement wave in the medium is given by y = 2cos( 2πx −100πt + π2 ) then equation of pressure waves will be (B → Bulk modulus of medium)
(А) P= 4Bπ sin(2πx− 100πt)
(В) P= 4Bπ sin(2πx+ 100πt)
(C) P= 4Bπ cos(2πx− 100πt)
(D) P= 4Bπ cos(2πx+ 100πt)
View SolutionSound wave pressure Equation and Displacement Equation
View SolutionThe equation y=Asin2(kx−ωt) represents a wave with
View SolutionA wave y=asin(ωt−kx) on a string meets with another wave producing a node at x=0. Then the equation of the unknown wave is
View SolutionEquation of motion in the same direction is given by y1=Asin(ωt−kx), y2=Asin(ωt−kx−θ). The amplitude of the medium particle will be
View Solution
