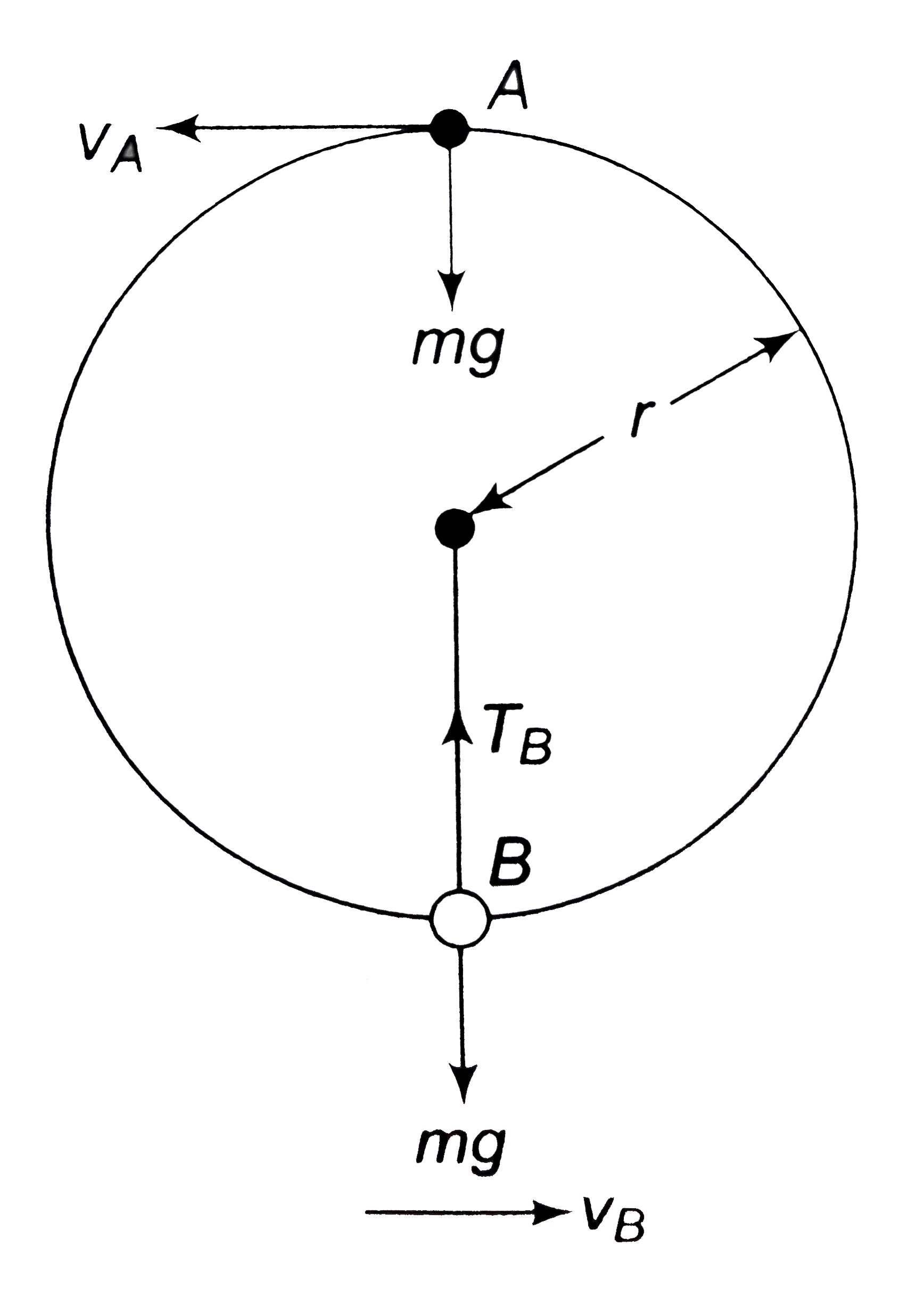
A stone tied to a string is rotated with a uniform speed in a vertical plane. If mass of the stone is m, the length of the string is r and linear speed of the stone is v when the stone is at its lowest point, then the tension in the string will be
(g= acceleration due to gravity)
mv2r+mg
mv2r−mg
mvr
mg
The correct Answer is:A
For a stone of mass m and length of string r at the point B, weight mg acts vertically downwards. While tension TB acts vertically upward. Their resultant provides the necessary centripetal force, that is
TB−mg=mv2r
⇒TB=mv2r+mg
This is the tension of string at lowest point.
Topper's Solved these Questions
- MOCK TESTBOOK - A2ZCHAPTER - MOCK TESTEXERCISE - General Kinematics
30 Videos
- MOCK TESTBOOK - A2ZCHAPTER - MOCK TESTEXERCISE - Motion With Constant Acceleration
15 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - A2ZCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Chapter Test
29 Videos
- MOTION IN TWO DIMENSIONBOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Chapter Test
29 Videos
Similar Questions
A stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
View SolutionA 2 kg stone at the end of a string 1 m long is whirled in a vertical circle at a constant speed. The speed of the stone is 4m/sec . The tension in the string will be 52 N , when the stone is
View Solution
Knowledge Check
A stone tied to a string is rotated in a circle. If the string is cut, the stone flies away from the circle because
AA centripetal force acts on the stoneBA centripetal force acts on the stoneCOf its inertiaDReaction of the centripetal forceA stone tied to a string is rotated a vertical circle. The minimum speed of the stone during a complete vertical circular motion.
Ais independent of the mass of the stoneBis independent of the length of the stringCdecreases with increasing mass of the stoneDdecreases with increasing length of the stringIF a stone is tied to one end of the string and whirled in verticle circle, then the tension in the string at the lowest point is equal to
Acentripetal forceBthe difference between centripetal force and weight of the stoneCthe addition of the centripetal force and weight of the stoneDweight of the stone
A stone tied with a string, is rotated in a vertical circle. The minimum speed with which the string has to be rotated
View SolutionA stone is tied to one end of a steing and rotated in horizontal circle with a uniform angular velocity. The tension in the string is T, if the lrngth of the string is halved and its angular velocity is doubled , the tension in the string will be
View SolutionA stone of a mass m tied to a string of length /is rotated in a circle with the other end of the string as the centre. The speed of the stone is V. If the string breaks, the stone will
View SolutionA 2 kg stone at the end of a string 1 m long is whirled in a vertical circle. At some point its speed is 4m/s. The tension of the string is 51.6 newton. At this instant the stone is :
View SolutionA stone is tied to a string of length l and is whirled in a vertical circle with the other end of the string as the centre. At a certain instant of time, the stone is at its lowest position and has a speed u. The magnitude of the change in velocity as it reaches a position where the string is horizontal (g being acceleration due to gravity) is
View Solution
