Is the position of image same as the position of object when object and image sizes are equal in a mirror?
To determine if the position of the image is the same as the position of the object when the object and image sizes are equal in a mirror, we can follow these steps:
1. Understanding the Concept of Mirrors:
- In a plane mirror, the image formed is virtual and upright. The distance of the image from the mirror is equal to the distance of the object from the mirror.
2. Define the Heights:
- Let the height of the object be h1 and the height of the image be h2. According to the question, we have h1=h2.
3. Magnification Formula:
- The magnification m of a mirror is given by the formula:
m=h2h1
- Since h1=h2, we can substitute:
m=h1h1=1
4. Relating Magnification to Distances:
- The magnification can also be expressed in terms of the distances of the object and image from the mirror:
m=−vu
- Where v is the distance of the image from the mirror and u is the distance of the object from the mirror.
5. Setting Up the Equation:
- Since we found that m=1, we can equate:
1=−vu
- This implies:
v=−u
6. Conclusion about Positions:
- The negative sign indicates that the image is on the opposite side of the mirror compared to the object. However, the magnitudes of v and u are equal, meaning the distances are the same.
- Therefore, the position of the image is the same as the position of the object, confirming that the statement is true.
Final Answer:
Yes, the position of the image is the same as the position of the object when the object and image sizes are equal in a mirror.
---
- In a plane mirror, the image formed is virtual and upright. The distance of the image from the mirror is equal to the distance of the object from the mirror.
- Let the height of the object be h1 and the height of the image be h2. According to the question, we have h1=h2.
- The magnification m of a mirror is given by the formula:
m=h2h1
- Since h1=h2, we can substitute:
m=h1h1=1
- The magnification can also be expressed in terms of the distances of the object and image from the mirror:
m=−vu
- Where v is the distance of the image from the mirror and u is the distance of the object from the mirror.
- Since we found that m=1, we can equate:
1=−vu
- This implies:
v=−u
- The negative sign indicates that the image is on the opposite side of the mirror compared to the object. However, the magnitudes of v and u are equal, meaning the distances are the same.
- Therefore, the position of the image is the same as the position of the object, confirming that the statement is true.
Yes, the position of the image is the same as the position of the object when the object and image sizes are equal in a mirror.
Topper's Solved these Questions
- REFLECTION AND REFRACTIONBOOK - PRADEEPCHAPTER - REFLECTION AND REFRACTIONEXERCISE - Short Q/A (3 marks)
35 Videos
- REFLECTION AND REFRACTIONBOOK - PRADEEPCHAPTER - REFLECTION AND REFRACTIONEXERCISE - long Q/A
7 Videos
- REFLECTION AND REFRACTIONBOOK - PRADEEPCHAPTER - REFLECTION AND REFRACTIONEXERCISE - long answer question
9 Videos
- MAGNETIC EFFECTS OF ELECTRIC CURRENTBOOK - PRADEEPCHAPTER - MAGNETIC EFFECTS OF ELECTRIC CURRENTEXERCISE - Mock Test
21 Videos
- SOURCES OF ENERGYBOOK - PRADEEPCHAPTER - SOURCES OF ENERGYEXERCISE - Mock Test
20 Videos
Similar Questions
Knowledge Check
The object or image distance is taken as positive
Aif the length is measured opposite to the direction of the incident ray.Bif the length is measured in the direction of the incident ray.Cif the length is measured opposite to the direction of the refracted ray.DNone of theseFor any position of an object, image formed in a convex mirror is.
AvirtualBerectCsmaller in sizeDas far behind the mirror as the object is in frontA concave mirror of focal length 15 cm forms an image having twice the linear dimensions of the object. The position of the object when the image is virtual will be
A22.5 cmB7.5 cmC30 cmD45 cm
A diverging mirror of radius of curvature 40 cm forms an image which is half the height of the object. Find the object and image positions.
View SolutionFollowing figure illustrates the ray diagram for the formation of image by a concave mirror. The position of the object is beyond the centre of curvature of the concave mirror. On the basis of given diagram .
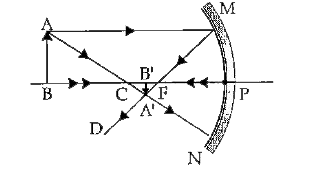
An image formed by concave mirror is virtual, when the object is placed:
View SolutionA concave mirror of focal length produces an image m times the size of the object. If image is real, then the distance of the object from mirror is
View SolutionAn object is placed in front of a mirror. Arrange the following steps in sequential order to determine the nature of the mirror.
(A) Check whether the image formed is virtual or real.
(B) Check whether the virtual image formed is dimished, magnified or same size as that of the object.
(C) If the image formed is real, the mirror used is concave.
(D) If a magnified vritual image is formed, the mirror is concave, if a dimished virtual image is formed, the morror is convex and if size of the image is equal to the size of the object, plane mirror is used.
View SolutionAn object is placed in front of a mirror. Arrange the following steps in sequential order to determine the nature of the mirror.
(A) Check whether the image formed is virtual or real.
(B) Check whether the virtual image formed is dimished, magnified or same size as that of the object.
(C) If the image formed is real, the mirror used is concave.
(D) If a magnified vritual image is formed, the mirror is concave, if a dimished virtual image is formed, the morror is convex and if size of the image is equal to the size of the object, plane mirror is used.
View Solution