The air if filled in a balloon and the volume of balloon increases gra

Which gas is filled in the balloon?
AHydrogen
BCarbon dioxide
CHelium
DOxygen
A balloon is pumped at the rate of $a$ $c m^{3}$ /minute. The rate of increase of its surface area when the radius is $b$ $c m$ , is
A $\frac{2 a^{2}}{b^{4}} c m^{2} / min$
B $\frac{a}{2} b c m^{2}$ /min
C $\frac{2 a}{b} c m^{3}$ /min
DNone of these
A conducting bolloon of the radius a is charged to potential $V_{0}$ and held at a large height above the earth ensures that charge distribution on the surface of the balloon remains unaffected by the presence of the earth. It is connected to the earth through a resistance R and a value in the balloon is opened . The gas inside the balloon escapes from value and the size of the balloon decreases. The rate of decrease in radius of the balloon is controlled in such a manner that potential of the balloon remains constant. Assume the electric permittivity of the surrounding air equals to that of free space $(ε_{0})$ and charge cannot leak to the surrounding air.

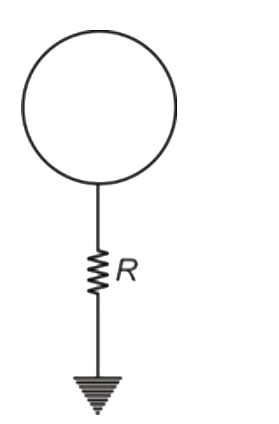
The rate at which radius r of the balloon changes with time is best represented by the equation
A $\frac{d r}{d t} = \frac{1}{4 π ε_{0} R}$
B $\frac{d r}{d t} = - \frac{1}{4 π ε_{0} R}$
C $\frac{d r}{d t} = \frac{1}{4 π ε_{0} a R}$
D $\frac{d r}{d t} = - \frac{r}{4 π ε_{0} a R}$

The air if filled in a balloon and the volume of balloon increases gradually. Find the rate of increase of volume of balloon with radius when of balloon becomes 30 cm.